利用矩阵初等变换求二维射影变换
周明旺
(连云港师范高等专科学校 数学与信息工程学院,江苏 连云港 222006)
二维射影变换是高等几何的核心内容之一,由无三点共线的四对对应点唯一确定。然而其射影变换式的求解在教材中采用的是由12 个线性方程求13 个未知量比值的方法,计算量很大。基于上述原因另辟新径,利用矩阵的初等变换知识给出了二维射影变换基本定理的一种新证法,进而给出二维射影变换的矩阵算法。这样以来不单简化了计算,更重要的是对于密切学科间的渗透、思想观念的更新、思维方法的训练、探究能力的培养等方面起着重要作用。[1]
1 预备知识
定义1 设在点场π 与π/上各建立了齐次射影坐标系,x = (x1,x2,x3),x/= (x/1,x/2,x/3)分别是其上点的射影坐标,如果映射φ:π →π/可以表示成
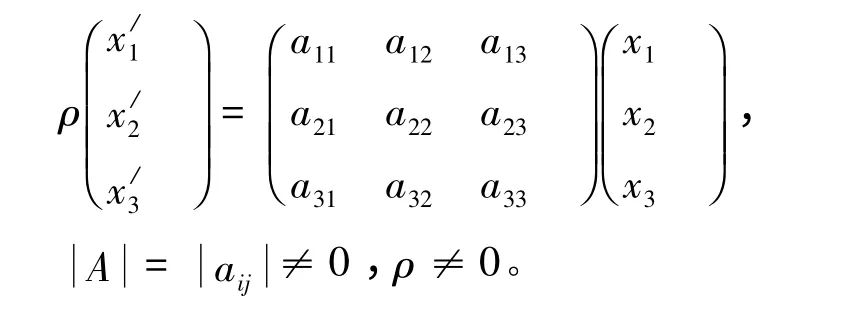
则称φ 是π 到π/的二维射影对应。特别地,若π/= π,则称φ 是π 上的二维射影变换。[2]
引理1 设A,B,C 为平面上不共线三点,其齐次坐标分别为a,b,c,则平面上任一点的齐次坐标可以表示为la +mb +nc,其中l,m,n ∈R,且l2+m2+ n2≠0 。[2]
定义2 设A,B,C,D 为平面上无三点共线的四点,适当选取其齐次坐标分别为a,b,c,d,若d= a+b+c,则称a,b,c,d 为点A,B,C,D 的规范化齐次坐标。
2 主要结果

其中l,m,n ∈R,且lmn ≠0 ,
则la,mb,nc,d 是A,B,C,D 的规范化齐次坐标。
证明:因为对矩阵施行初等行变换不改变列向量的线性关系。[3]
对于

即d = la+mb+nc,所以la,mb,nc,d 是A,B,C,D 的规范化齐次坐标。
定理2 射影平面上任意的两个四点组(其中各组内均无三点共线),则存在唯一的二维射影变换。[4]
下证A 的存在性与唯一性。
由φ P( )i = P/i,i = 1,2,3,4。则
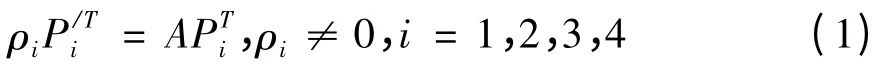
由引理1,存在全不为零的λ1,λ2,λ3使得P4= λ1P1+ λ2P2+ λ3P3,同理存在全不为零的使得于是
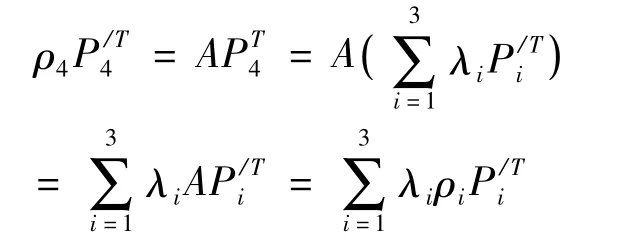
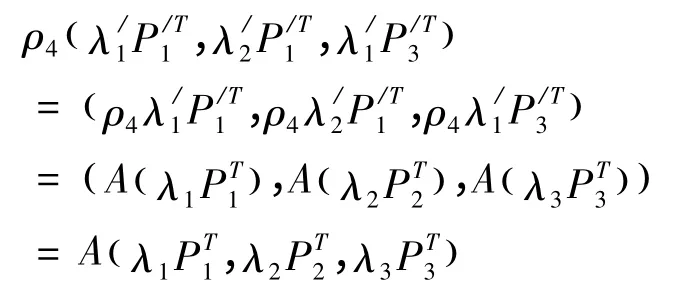
而对于ρ4的不同取值,结合点的齐次坐标的性质知:射影变换是相同的,即射影变换唯一。
推论 设P1,P2,P3,P4与,,,为射影平面上任意的四点组 (其中各组内均无三点共线),若其坐标2,3,4 均为规范的齐次坐标,则存在唯一射影变换且其中
3 应用举例
例1 在点场π 上设四点P10,0,( )1 ,P21,0,( )0 ,P3-1,1,( )1 ,P41,1,( )0 依次对应于四点P/11,-1,( )1 ,P/2 2,1,( )0 ,P/3-2,0,( )1 ,P/41,3,( )0 ,求射影变换式。解:易知两四点组的坐标均为非规范化齐次坐标。
知P4=-P1+2P2+ P3。
例2 在点场π 上设四点P11,0,( )0 ,P20,1,( )0 ,P30,0,( )1 ,P41,1,( )1 依 次 对 应 于 四 点P/11,0,( )1 ,P/2 0,1,( )1 ,P/3-1,-1,-(1 ,P/4 0,0,( )1 ,求射影变换式。)
易见,利用矩阵算法求解二维射影变换较之利用解线性方程组的方法,过程简洁了许多。更重要的是密切了与高等代数之间的联系,这对于探究能力的培养意义深远。文中所述方法对于n(n ≥3)数组 (x1,x,…,xn)的线性变换都是可行的,并且n 越大其计算简便的优越性体现得越突出。[5]
[1]周明旺. 矩阵对角化的高等几何解释[J]. 宜春学院学报,2013,35(9):18-23
[2]梅向明,刘增贤,林向岩. 高等几何[M]. 北京:高等教育出版社,1983:125-130
[3]王萼芳,石生明. 高等代数(第三版)[M]. 北京:高等教育出版社,2003:126-134
[4]周兴和. 高等几何[M]. 科学出版社,2007:99-100
[5]孙克宽. 求二维射影变换式的矩阵算法[J]. 高等函授学报,2000,13(3):8-10

