立体几何中线段长度的最值问题
◇ 北京 陶 军(特级教师)
立体几何中的最值问题是高中数学的难点,这类问题包括求长度、角度、面积和体积等最值,而有关线段长度的最值问题是最基本的问题,求解这类问题的通法是几何法和向量法,本文进行例析.
例1如图1所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为BC,CC1的中点,点P是侧面BCC1B1上一点,A1P∥平面AEF,则线段A1P长度的最小值是________.
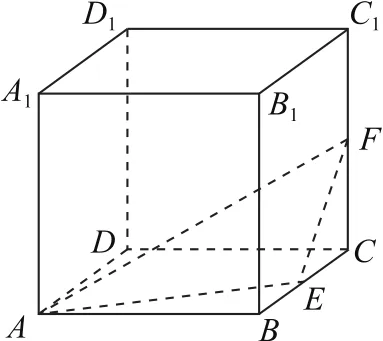
图1
分析1因为点A1是定点,欲求线段A1P长度的最小值,所以需确定动点P的位置.因为直线A1P绕点A1转动时总和平面AEF保持平行,所以动直线A1P形成的平面与侧面BCC1B1相交,点P就在它们的交线l上.因为交线l平行于平面AEF,侧面BCC1B1与平面AEF的交线是EF,所以l∥EF.怎样找到交线l的位置呢?只需先找到点P,它是侧面BCC1B1上的一个点.考虑到E为BC的中点,取B1C1的中点P1,可知A1P1∥AE,则A1P1∥平面AEF,而过点P1且与EF平行的直线是唯一的,就是交线l,显然l过线段B1B的中点P2,点P的轨迹是线段P1P2,所以求线段A1P长度的最小值转化为求点A1到P1P2的距离.
解法1(几何法)如图2所示,取B1C1的中点P1,因为P1E∥A1A,且P1E=A1A,所以四边形P1EAA1是平行四边形,所以A1P1∥AE.取线段B1B的中点P2,则P1P2∥FE,又因为AE与EF相交于点E,所以平面A1P1P2∥平面AEF,由于点P在平面A1P1P2上,又在侧面BCC1B1上,故点P的轨迹是线段P1P2.在等腰△A1P1P2中,A1P1=.取P1P2的中点M,则A1M⊥P1P2,于是,所以线段A1P长度的最小值是.
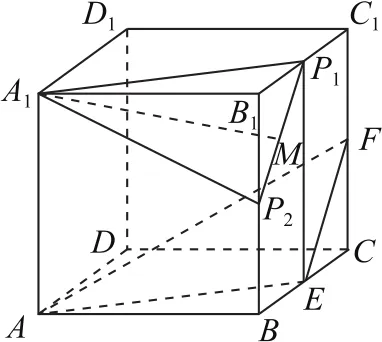
图2
分析2因为点A1是定点,线段A1P的长度由动点P的位置决定,确定点P的位置可以引入坐标,为此考虑建立适当的空间直角坐标系,设出动点P的坐标,列出长度的表达式,借助函数的思想求A1P的最小值.
解法2(向量法)如图3所示,以点D为原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,则A1(2,0,2),因为点P是侧面BCC1B1上一点,可设点P的坐标(x,2,z)(0≤x≤2,0≤z≤2),故
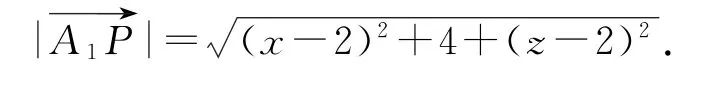
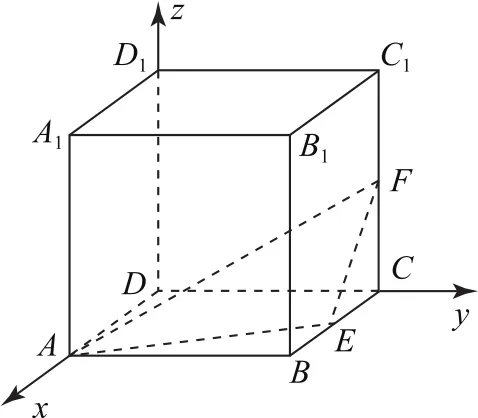
图3
设平面AEF的法向量n=(x0,y0,z0),因为
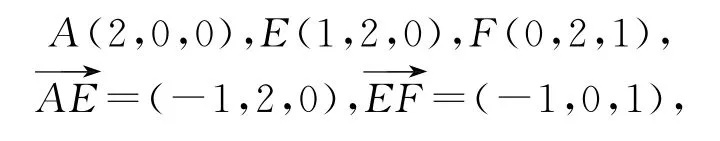
所以
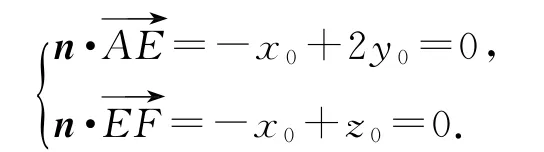
令y0=1,则x0=z0=2,n=(2,1,2).因为A1P∥平面AEF,所以n与垂直,故
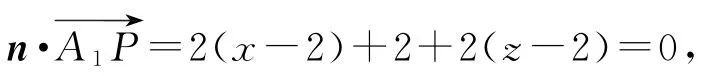
化简得x+z=3,因为0≤z≤2,所以0≤3-x≤2,且0≤x≤2,解得1≤x≤2.把z=3-x代入的表达式,整理得故当取得最小值.
例2如图4所示,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为________.
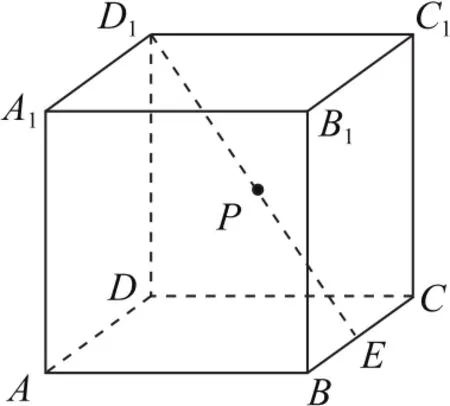
图4
分析1求点P到直线CC1的距离的最小值,就是找点P到直线CC1的垂线段PQ长度的最小值.求线段PQ的长度涉及空间上两个动点长度的距离问题,不易处理.注意到CC1⊥平面ABCD,PQ⊥CC1,则PQ∥平面ABCD.因此,我们可以把PQ正投影在平面ABCD上,点P在平面ABCD上的正投影H落在线段DE上,点Q在平面ABCD上的正投影是点C,于是PQ=HC,求PQ的最小值转化为在平面ABCD上求定点C与线段DE上的动点H之间距离的最小值,就是求定点C到DE的距离.
解法1(几何法)如图5所示,过点P作PQ⊥CC1,Q为垂足,因为CC1⊥平面ABCD,所以PQ∥平面ABCD,过点P作PH⊥DE,H为垂足,则PH⊥平面ABCD,所以PH∥QC,且PQ∥HC,QC⊥HC,故四边形PQCH是矩形,PQ=HC,在Rt△CDE中,当CH⊥DE时,CH长度最小,因为,所以,故点P到直线CC1的距离的最小值为.
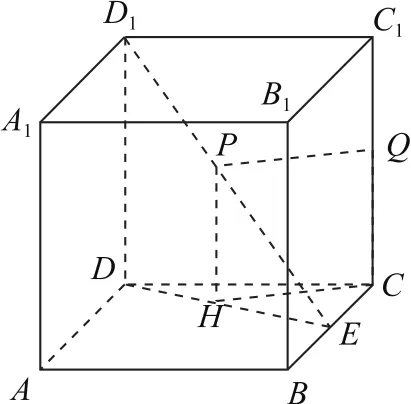
图5
分析2设点P到直线CC1的距离为PQ,因为P,Q分别在线段D1E和CC1上,故可以引入两个变量控制点P,Q的位置.
解法2(向量法)如图6所示,以D为原点,DA,DC,DD1分别为x,y,z轴建立空间直角坐标系,则D1(0,0,2),E(1,2,0),C1(0,2,2),C(0,2,0),由于点P在线段D1E上,可设由此得点P的坐标为 (1-λ,2-2λ,2λ).
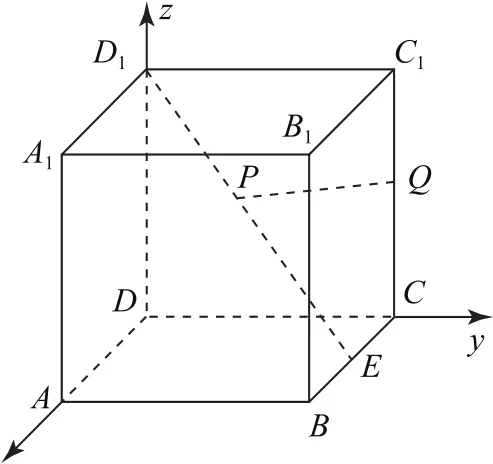
图6
过点P作PQ垂直于CC1,Q为垂足,设点Q的坐标,即
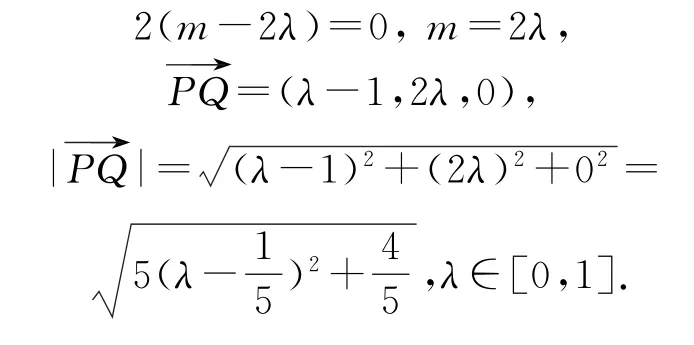
综上所述,利用几何法求线段长度的最值,要点是先用立体几何知识确定动点的轨迹,再用平面几何知识求最值;利用向量法求线段长度的最值,要点是建立适当的坐标系,设出动点坐标,建立线段长度的表达式,借助向量知识把题目中的几何条件合理转化为代数条件,找到动点坐标的关系,把线段长度的表达式转化为一元函数,用函数的思想求最值.

