“模型”在立体几何试题中的应用剖析

◇ 江西 章建荣 龙光鹏

立体几何试题在高考中旨在考查学生直观想象和逻辑推理素养.立体几何中有许多几何模型,其中长方体模型是学生认识空间点、线、面位置关系的最佳模型,所以高考试题的命制中越来越关注长方体模型.立体几何中学生易掌握的简单几何体是长方体,其几何性质和直观的几何结构学生更容易掌握和理解,并且在长方体中添加辅助线,可以构建各种线线关系、线面关系、面面关系,所以在遇到点、线、面的问题时,应该巧妙合理地构造出长方体模型或截面模型加以解决,使得复杂的问题变得更易理解.

1 典例剖析

例1(2019年全国卷Ⅲ理8)如图1,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( ).

A.BM＝EN,且直线BM,EN是相交直线

B.BM≠EN,且直线BM,EN是相交直线

C.BM＝EN,且直线BM,EN是异面直线

D.BM≠EN,且直线BM,EN是异面直线

分析本题主要考查空间直线的位置关系,既有定性分析,又有定量研究.

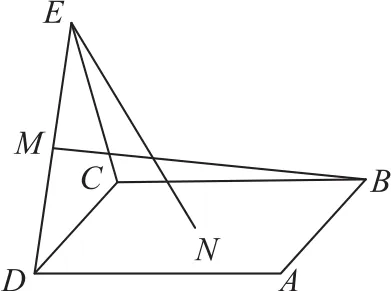
图1

解如图2,根据题干信息建立长方体模型.由长方体模型易知M,N分别是ED,BD的中点,则MN∥EB,又知M,N,B,E四点共面,所以可以准确判断出直线BM,EN是相交直线,且BM≠EN.故选B.

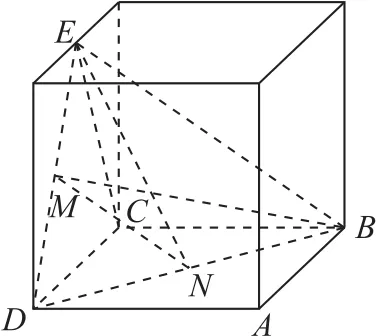
图2

点评

借助长方体模型,易知MN∥EB,则四边形MNBE为梯形,同时,结合四边形ABCD为正方形,△ECD为等边三角形,则BD＝ 2DE,故梯形MNBE不是等腰梯形,再进行几何图形的定性分析与研究.依托长方体模型,采用降维的方式,将立体几何中的问题转化为平面问题,再分析问题、解决问题.结合梯形MNBE不是等腰梯形,所以BM≠EN.进一步将问题转化为定量研究.

例2(2018年全国卷Ⅰ理12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为( ).

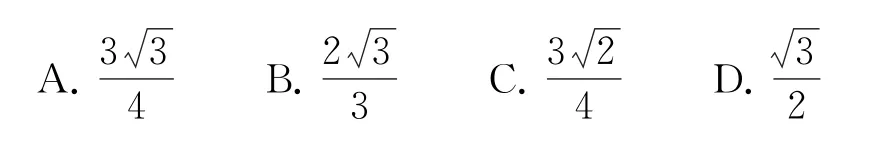
分析本题主要考查动态截面的最值、面面平行的性质定理、线面角等知识,考查了学生的空间想象能力和转化与化归思想,同时,旨在考查学生的直观想象和数学运算素养.

解法1如图3所示,每条棱所在直线与平面α所成的角相等时,平面α与体对角线垂直,则当截面为六边形时,面积会比截面为三角形时的面积大.

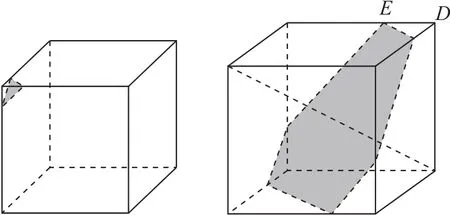
图3

探究当截面为六边形时截面的面积S,设ED＝a,则可以分别求出各边长(如图4),所以

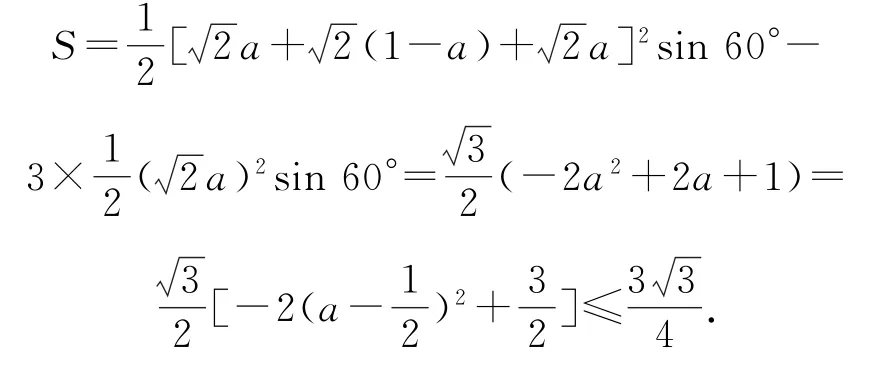
故选A.

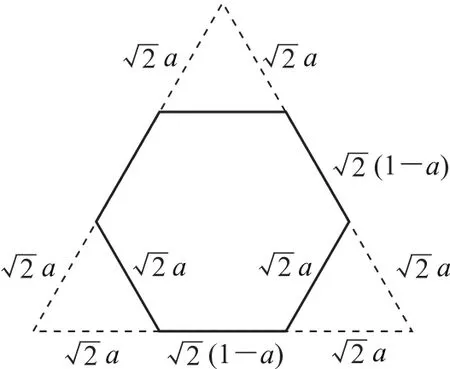
图4

解法2易知,当截面为正六边形时,截面面积最大,如图5所示.所以故选A.

点评

求解立体几何问题时,直观想象素养是不可或缺.但学生观察几何图形的时候,往往缺乏对几何图形的直观感知,导致解题产生困惑.若学生能够较好地理解当截面为正六边形的时候,截面面积最大,问题就容易获解了.

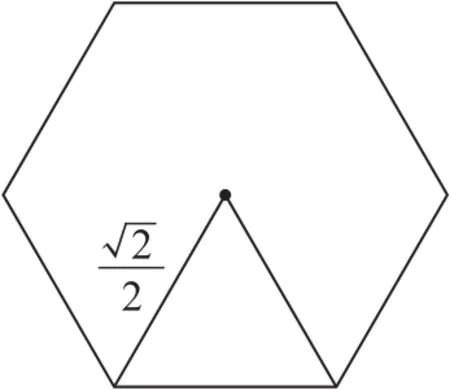
图5

例3设点P是棱长为1的正方体ABCDA1B1C1D1对角线BD1的中点,平面α过点P,且与直线BD1垂直,则平面α与正方体ABCDA1B1C1D1的表面的交线长为________.

分析本题主要考查截面的周长、线面垂直的性质定理,考查了学生的空间想象能力,同时,旨在考查学生的直观想象和数学运算素养.

解如图6所示,将立体问题平面化,得到如图7的平面图形.设∠DBD1＝θ,则,所以,因为,所以即E为BD的四等分点,所以截面为正六边形,其周长为.

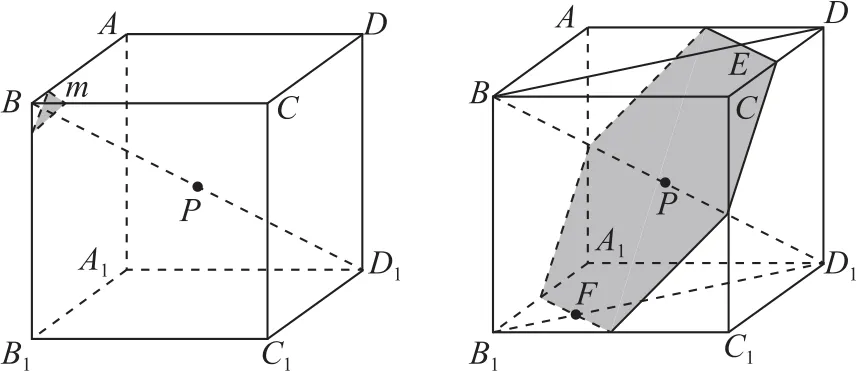
图6

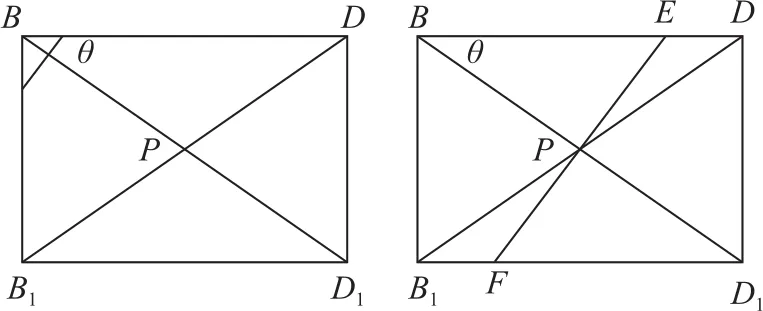
图7

点评

解题时,要重视对文字语言、图形语言和符号语言的理解,故教学中,教师应注意引导学生结合长方体模型,学会将文字语言转化为图形语言和符号语言,使学生准确地使用数学语言表述几何对象的位置关系.同时,在教学中要利用类比、联想等方法,辨别平面图形和立体图形的异同,理解两者的内在关系,并逐渐感悟到要将空间问题转化为平面问题,这是处理立体几何问题的重要思想.

例4如图8所示,在四面体ABCD中,AB＝CD＝2,AC＝BD＝,AD＝BC＝,E,F分别为AD,BC的中点.若用一个与直线EF垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到的一个多边形截面,则该多边形截面面积的最大值为( ).

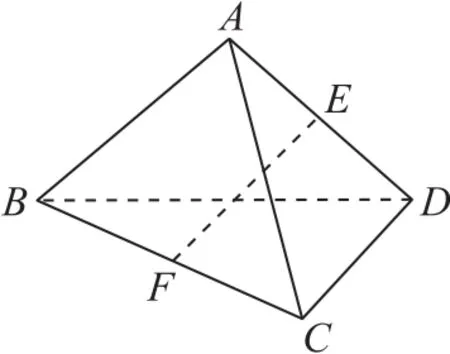
图8

分析本题考查四面体的截面问题、线面的位置关系和线面垂直的性质定理,旨在考查学生的空间想象能力和转化与化归能力,培养学生的直观想象和数学运算素养.

解在四面体ABCD中,AB＝CD＝2,AC＝,将四面体放到一个长方体中,其中长方体的长为,宽为,高为1.如图9所示,因为EF⊥平面α,故截面为平行四边形MNKL,可得,设异面直线BC与AD所成的角为θ,则sinθ＝sin∠LKN,可知,所以当且仅当NK＝KL时,等号成立.故选B.

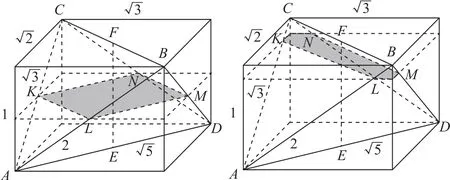
图9

点评

我们知道,几何体组成的基本元素是点、线、面,解决几何体中元素之间的等量和位置关系时,首先要寻求几何体的模型,准确地把握几何体中元素的关系,依托模型,提升解题能力,促进逻辑推理素养的提升.

例5已知正方体ABCD-A1B1C1D1的棱长为3,垂直于棱AA1的截面分别与面对角线A1D,A1B,C1B,C1D相交于点E,F,G,H四点,则四棱锥A1-EFGH体积的最大值为________.

分析主要考查动态几何体的体积最值问题,涉及线面垂直的性质定理和三次函数求最值的方法.

解如图10所示,易知四边形EFGH为矩形,△A1EF,△BFG为等边三角形,设EF＝x,则FG＝,设棱锥的高为h,则,

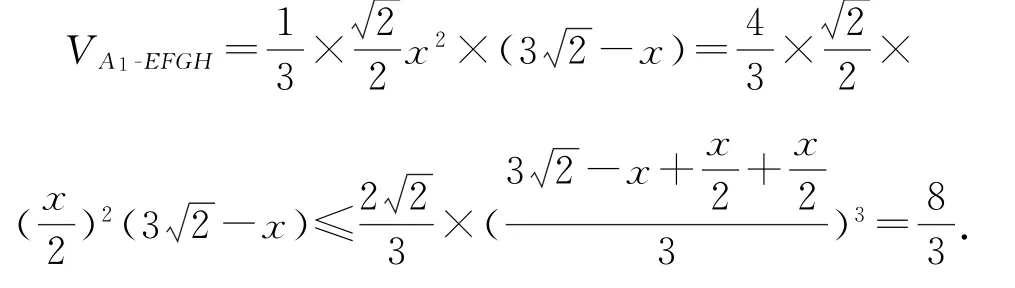
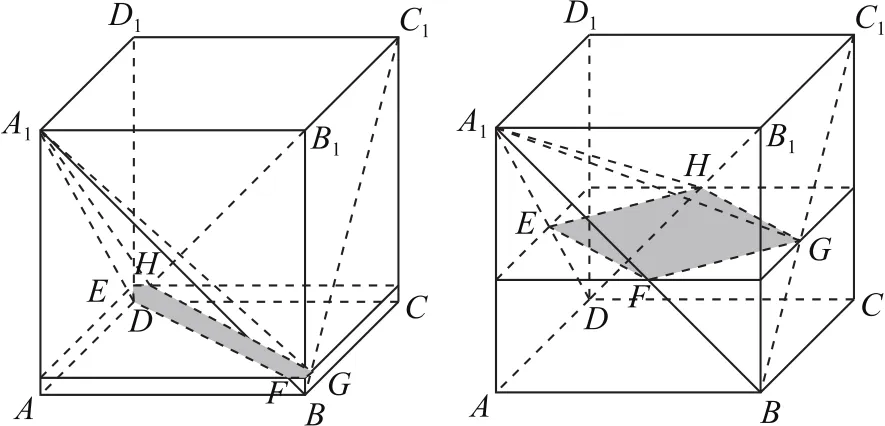
图10

点评

通过对空间图形的观察、实验、操作和思辨,使学生了解平行、垂直关系的基本性质以及判定方法,空间想象能力的培养是立体几何教学的重点.

2 总结与反思

纵观近几年的高考试题可以发现,高考试题来源于教材,又高于教材.高考中的立体几何试题大多数是以长方体模型和截面模型为依托,考查学生的空间想象能力,关注学生的学科核心素养.

在立体几何中,长方体模型和截面模型是非常重要的两个模型,依托长方体模型和截面模型可以解决很多立体几何问题.同时,把空间问题转化为平面问题,也是求解立体几何问题的一种基本方法.作几何体的截面,既是将立体几何问题转化为平面问题的一个方法,也是理解空间点线面关系的一个很好的途径.

长方体模型和截面模型的研究,对于发展学生的空间想象能力,提升综合运用立体几何各方面的知识技能,提高学生的解题能力,都是十分有启发、有思考价值的题材.同时对学生进行空间几何体截面的作图等训练也是培养和发展学生核心素养的拓展课题.