两根“拐杖”(几何法与坐标法)“走路”

◇ 山东 张林德

几何法与坐标法是高中数学的重要方法,几何法“寓数于形”,将数学问题转化为几何问题,使问题形象直观,易于突破;坐标法“寓数于算”,将数学问题转化为运算问题,降低思维难度,易于解答.本文通过例题分析几何法与坐标法在平面向量、立体几何、解析几何中的作用,以期拓宽读者的解题思路,提高解题能力.

1 平面向量中的两根“拐杖”

例1如图1所示,在面积为1的平行四边形ABCD中,,则点P是直线AD上的动点,则的最小值为_______.

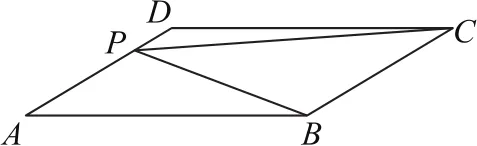
图1

解析

如图2所示,设AB＝m,BC＝n,因为该平行四边形面积为1,则所以

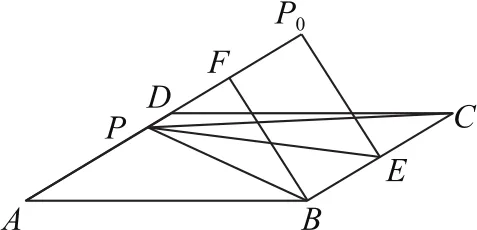
图2

拐杖1:几何法如图2所示,取BC的中点E,连接EP,过E作EP0⊥AD,垂足P0,过B作BF⊥AD,垂足为F,因为AD∥BC,所以

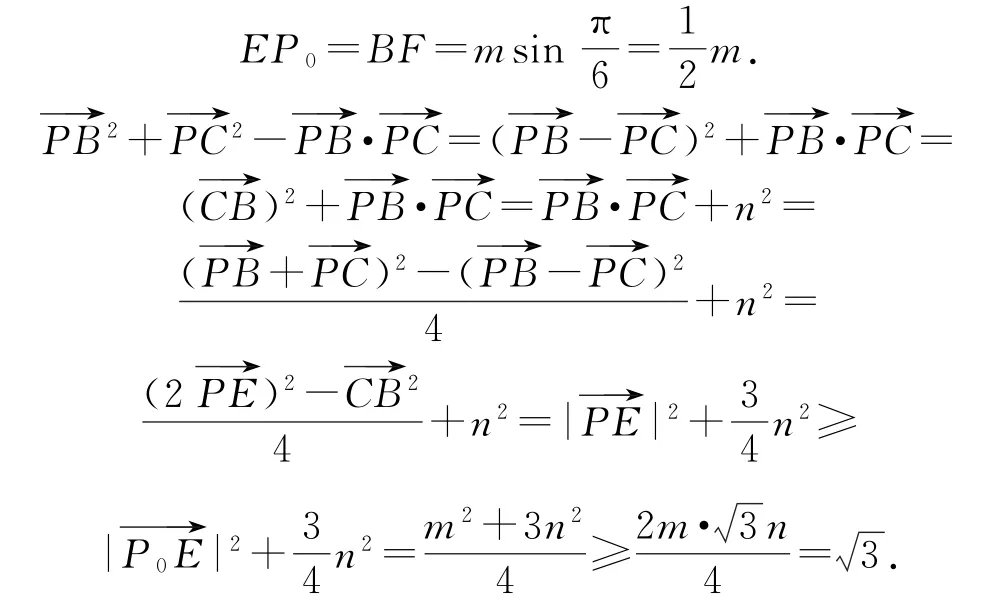
拐杖2:坐标法如图3所示,以A为原点,AB所在直线为x轴,建立平面直角坐标系.

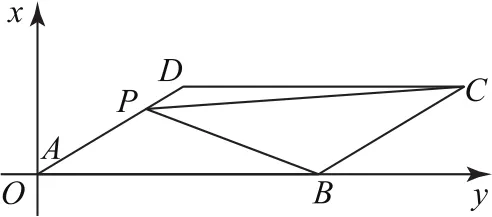
图3

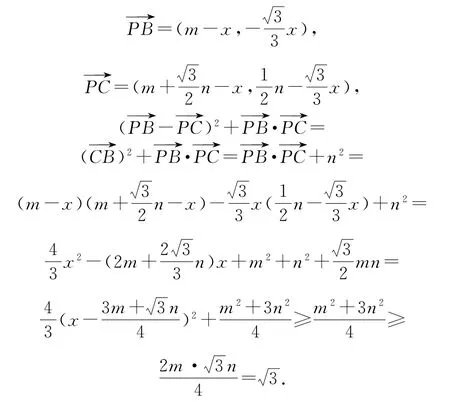
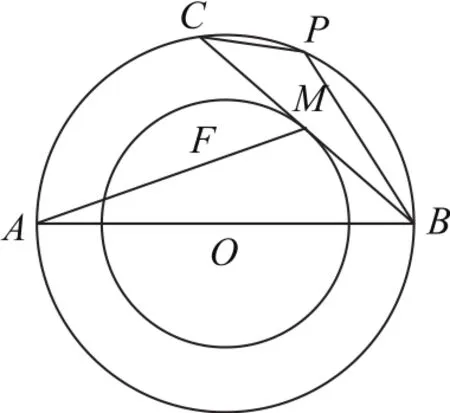
图4

例2如图4所示,两个同心圆O的半径分别为2和2,AB为大圆O的一条直径,过点B作小圆O的切线交大圆于另一点C,切点为M,点P为劣弧上的任意一点(不包括B,C两点),则的最大值是________.

解析

拐杖1:几何法如图5所示,作垂直于AM且与大圆O相切的直线,切点为D,该直线交AM的延长线于点E,过O作OF⊥AM,垂足为F,连接OD,PM,则OD⊥DE,OM⊥BM,M是BC的中点,四边形ODEF是矩形,FE＝OD＝2.

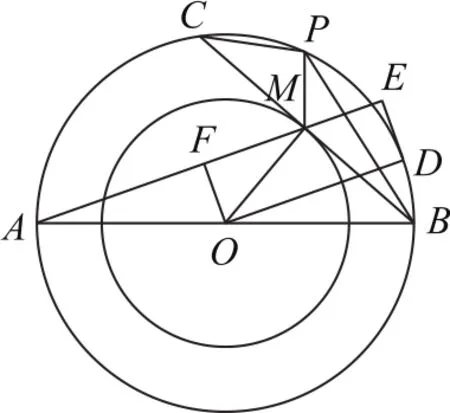
图5

在Rt△OMB中,因为OM＝ 2,OB＝2,所以∠BOM＝45°,∠AOM＝135°.

在△OMA中,

拐杖2:坐标法以O为原点,OB所在直线为x轴,过点O且与OB垂直的直线为y轴,建立平面直角坐标系,则A(－2,0),M(1,1),P(2cosα,2sinα),,

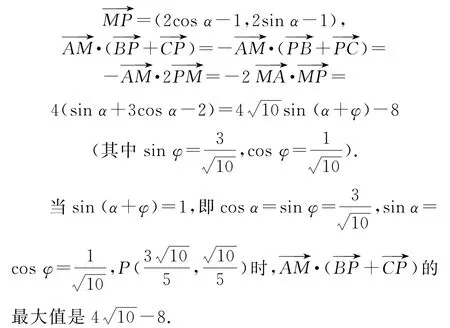
点评

通过以上两个例题我们发现,坐标法步骤更简单一些,因此向量问题能用坐标法解决就尽量优先使用坐标法.

2 立体几何中的两根“拐杖”

例3如图6所示,在四面体ABCD中,△ABC是斜边AB为2的等腰直角三角形,△ABD是以AD为斜边的等腰直角三角形,已知CD＝,点P,Q分别在线段AB和CD上,则PQ 的最小值为_______.

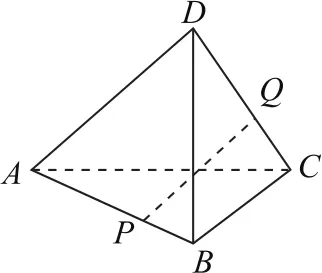
图6

解析

拐杖1:几何法

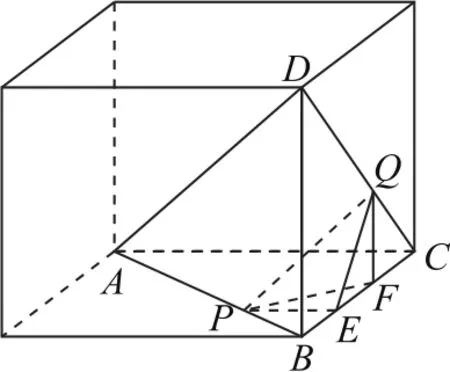
图7

如图7所示,为让图形直观,把四面体放在长方体ABCD中.当PQ为线段AB,CD的公垂线时,PQ取得最小值.(两条异面直线上两点间距离的最小值为公垂线段的长度).过P作PE⊥BC于E,过Q作QF⊥BC于F,连接QE,PF,则PE⊥平面BCD,QF⊥平面ABC,由三垂线定理的逆定理知,EQ⊥CD,FP⊥AB.设BE＝x,则,由△EFQ∽△DBC,.

拐杖2:代数法如图8,以B为原点,建立空间直角坐标系O-xyz,则所 以.

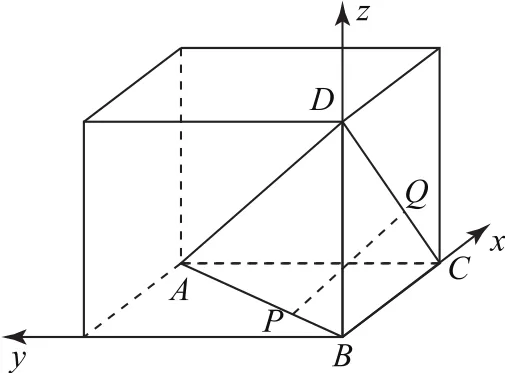
图8

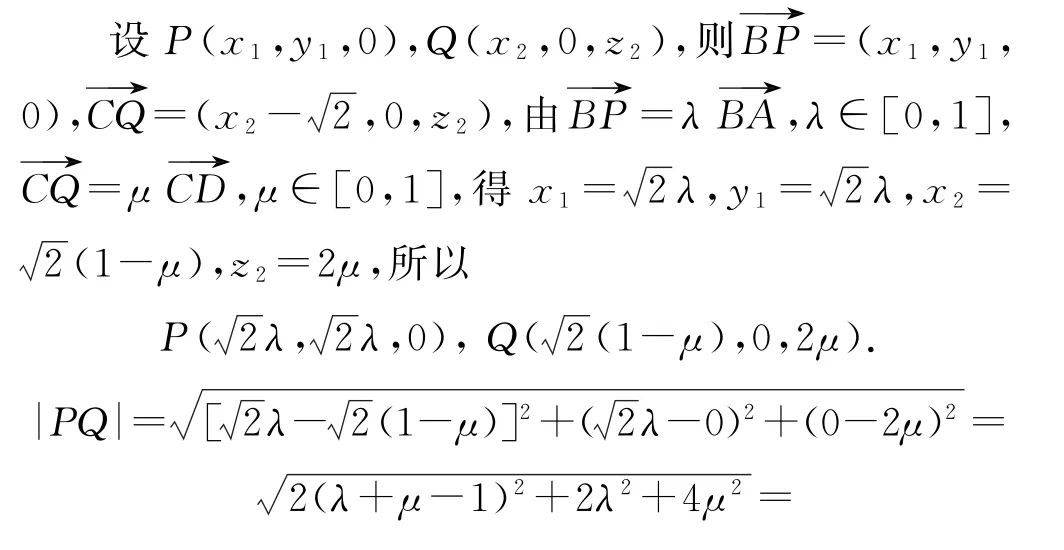
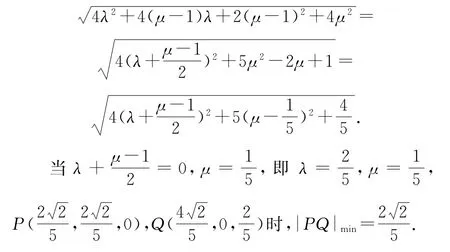
例4(2019年全国卷Ⅰ理18)如图9所示,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1＝4,AB＝2,∠BAD＝60°,E,M,N 分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;

(2)求二面角A-MA1-N的正弦值.

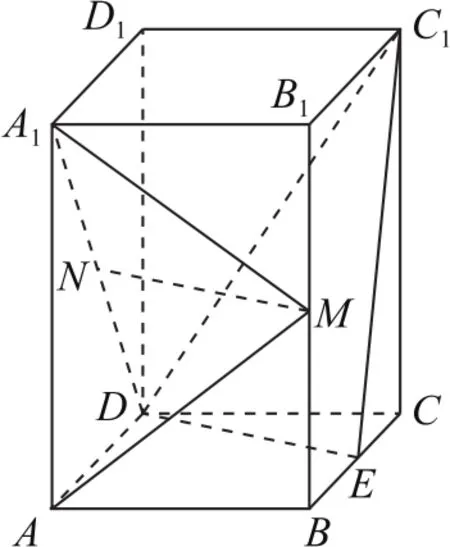
图9

解析

(1)略.

(2)拐杖1:几何法如图10所示,取AB的中点G,连接DG,过G作A1M的垂线,垂足为H,连接DH,DM,因为四边形ABCD是菱形,且 ∠BAD＝60°,所 以DG⊥AB,又因为ABCDA1B1C1D1是直四棱柱,所以平面ABB1A1⊥平面ABCD,从而DG⊥平面ABB1A1,DG⊥A1H,A1H⊥平面DGH,A1H⊥DH,所以∠DHG是二面角A-MA1-N的平面角.

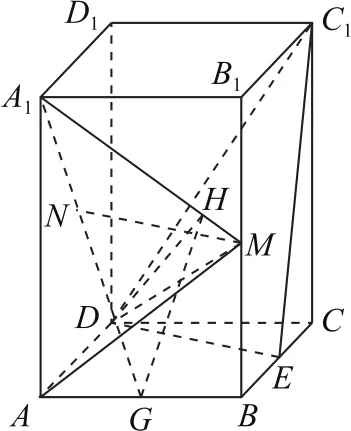
图10

拐杖2:代数法如图11所示,DE⊥BC,∠CDE＝30°,又∠ADC＝120°,∠ADE＝90°,以D为原点,DA,DE,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,,BE＝1,D(0,0,AB的中点为,所以平面AMA1法向量为.

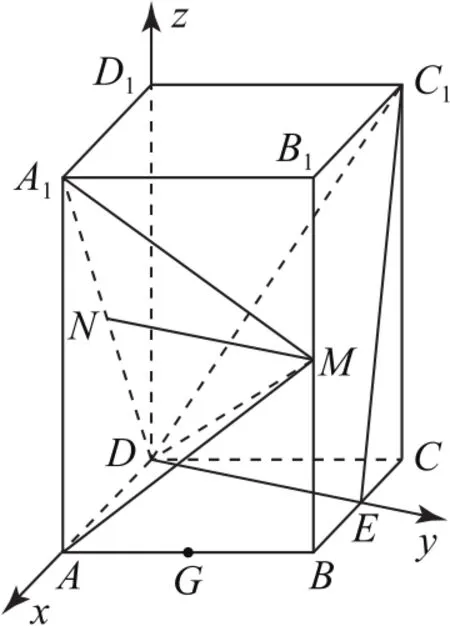
图11

设平面MA1N的法向量为n2＝(x,y,z).由

令z＝1,得x＝－2,y＝0,所以平面MA1N的法向量为n2＝(－2,0,1).

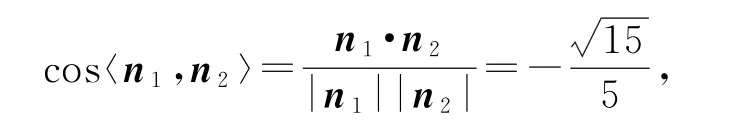
因为〈n1,n2〉∈[0,π],所以.

综上,二面角A-MA1-N的正弦值为.

点评

立体几何中的几何法实质上是将三维空间问题转化为二维平面问题,坐标法实质上是将立体几何问题转化为数的运算问题,二者体现的都是转化思想.

3 解析几何中的两根“拐杖”

例5已知抛物线C:y2＝2px(p＞0)过点(1,－2),经过焦点F的直线l与抛物线交于A,B两点,A在x轴上方,Q(－1,0),若以QF为直径的圆经过点B,则|AF|－|BF|＝( ).

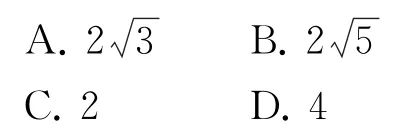
解析

拐杖1:几何法1由已知可得p＝2,设AB的倾斜角为α,则|AF|＝2＋|AF|cosα,即同理.

又因为以QF为直径的圆经过点B,所以BQ⊥BF,在Rt△FBQ中,|BF|＝2cosα.所以2cosα,即1－cos2α＝cosα.

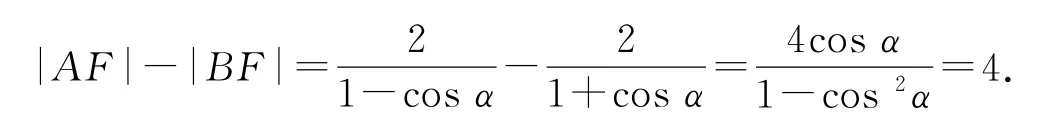
故选D.

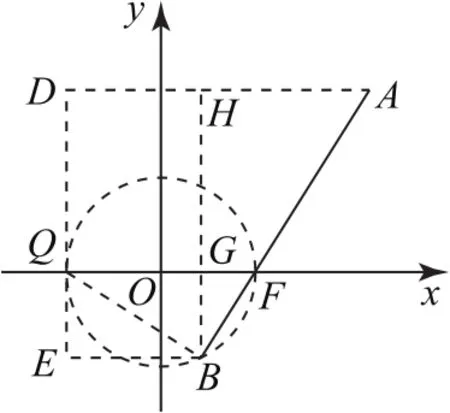
图12

拐杖1:几何法2已知抛物线C:y2＝2px(p＞0)过点(1,－2),所以4＝2p,抛物线C的方程为y2＝4x,F(1,0),Q在准线x＝－1上.如图12,过A,B作准线的垂线,垂足分别为D,E,过B作AD的垂线,垂足为H,交x轴于G,连接BQ,因为以QF为直径的圆经过点B,所以BQ⊥BF.

设|OG|＝n,|AF|－|BF|＝m.|OQ|＝|OF|＝1,|BE|＝|DH|＝|BF|＝|QG|＝n＋1,|GF|＝1－n.在Rt△FBQ中,由射影定理得(1＋n)2＝2(1－n),即1－n2＝4n.

拐杖2:代数法由已知可得p＝2,F(1,0),设直线AB的方程为y＝k(x－1),A(x1,y1),B(x2,y2),联立得k2x2－2(k2＋2)x＋k2＝0,x1x2＝1.

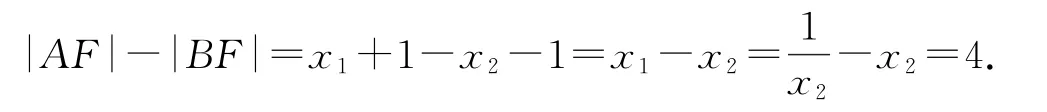
故选D.

例6如图13所示,已知双曲线b＞0)的左、右焦点分别为F1,F2,其右支上存在一点M,使得直线MF2平行于双曲线的其中一条渐近线,则双曲线C的离心率为( ).

解析

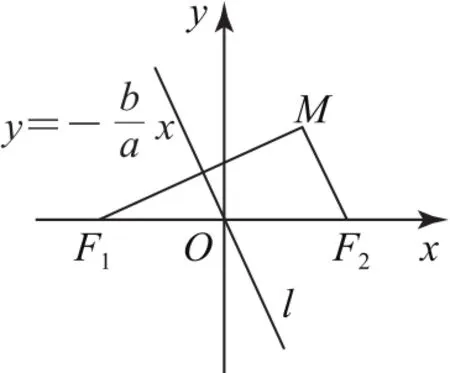
图13

拐杖1:几何法双曲线C的渐近线方程为,设MF2平行于直线则,从而

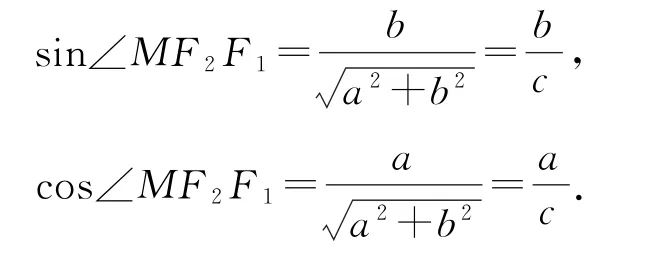
在Rt△F1MF2中,|F1F2|＝2c,所以

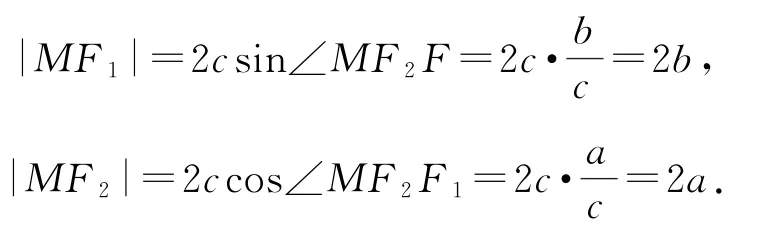
根据双曲线定义,得|MF1|－|MF2|＝2a,所以2b－2a＝2a,即b＝2a,所以离心率为

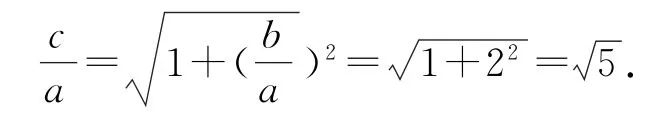
故选D.

拐杖2:代数法由得MF1⊥MF2,不妨设MF2平行于双曲线C的渐近线l:y＝,所以MF1⊥l,l是线段MF1的中垂线,则直线MF1的方程为,设MF1与l的交点为N,联立,解得x＝,又F1(－c,0),所以,由M在双曲线上,得化简得c2＝5a2,即离心率,故选D.

点评

解析几何是联系几何与代数的一门学科,是用代数方法解决几何问题的一门学科,解题的主要方法是坐标法,因为它具有几何的性质,有时用几何法可大大减少运算量,达到事半功倍的效果.

几何法形象直观,坐标法思路清晰,两种方法各有千秋、相辅相成、优势互补,有些题目用几何法简单,有些题目用坐标法简单,有些题目需要两种方法结合,因此只有熟练掌握这两种方法,才能游刃有余.