对高一数学学困转化的思考

刘曦文 吴林炎

摘 要：本文主要是分析了高一学生数学学习困难的原因，以及结合高一教学提出几个相应措施，讲述教师从哪些方面提高高一学生的数学成绩。

关键词：高一学生;数学学习;学习兴趣

提起数学，“难”这个字是首当其冲的，和小学、中学相比，高中数学的学习确实是不容易的，不仅要投入时间，还要思考，而事实上，在高中努力了，但成绩依旧不理想的学生大有人在。高一正是中学结束迈入高中的过渡阶段，当他们满怀憧憬、信心满满地开始高中的学习，经过一段时间学习，抽象和枯燥的感觉油然而生，数学学习困难的问题逐渐体现，从而开始对数学产生不自信，甚至是畏惧心理，也严重影响数学成绩的提高。高一作为高中学习的开始阶段，对整个高中的学习影响是巨大的。数学和其他科目不一样，知识环环相扣，很多高一的概念和思想在整个高中都是不可或缺的。

在高一树立信心，可以促进之后二年的学习;同样的，如果高一学习遇到了瓶颈，那么对往后学习的阻碍也是不容忽视的。

一、高一学生数学学习困难形成的原因

（一）学生心理不成熟

高一学生一般是十六岁，或十七岁，这正是青春期、叛逆期。这个时期的孩子心智不成熟，自我控制能力差，高中学习不同于中学学习，高中注重的是主动学习，积极思考，科学的学习计划，中学往往是学生围着教师转。在高中，则需要自我把控时间，把中学学习六科的时间分配到现在的九科，很多学生不能做到时间和科目上很好的平衡，导致学习效率低，学得苦却学不好。再者，现在的科技信息发达，手机对学生的影响不容小觑，学生除了学习，还要抵制电子设备对其的诱惑。

（二）初高中知识的差异

中学数学相对于高中而言，是较为简单的。

简单是具体。之前的计算，是具体的数字，现在开始逐渐出现字母，最后变为纯字母。中学数学知识一般都是接近生活实际，计算的是具体数值，学习数学是可以遵循感性认知，从自身出发找到理解知识的方法;高中数学则是抽象的，从高一入学第一节课的集合开始便是对学生思维有一定的要求，到后来更加抽象的函数（幂函数、指数函数、对数函数、三角函数），无一不是向学生呈现高中数学难理解的特点。

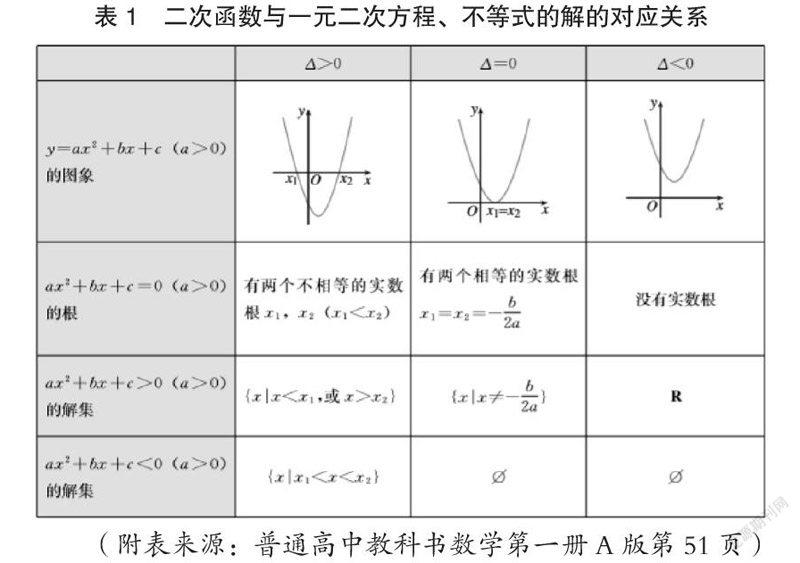
简单是内容少。中学知识的特点是题型少，而且还单一，教师对学生不易理解的点可以反复进行强化，而高中，一则需要挖掘中学知识的深度，二则还要学习新的概念，留旧的同时，还要取新。这样一来，高中便显现出难内容还多的特点。例如：第一册教材（普通高中教科书数学第一册A版）的第二章一元二次函数，方程和不等式中涉及的二次函数，中学对二次函数是有了解的，高中对其进行补充学习，加入了二次函数与一元二次方程不等式的解的对应关系。

（三）数学学习缺乏自信和耐心

在大部分人的眼中，数学是一门比较难的科目，所以学生在此观念的影响下便也认为数学是一门不好学的科目，对数学的学习，就缺乏了自信心，如若再遇上数学底子较薄弱的学生，那他对数学的期望值就会大幅度降低，对数学也就提不起学习的劲头。

数学学习注重基础，而基础需要按部就班，从最开始的概念慢慢过渡到应用，这个过程是单一的，学生容易没有耐心，刚开始学生还能规范书写，到后面便开始忽视条理性。艾宾浩斯的遗忘曲线规律提到，只有不断地重复才能把短期记忆变成长期记忆，新的概念只有記住了才是属于自身的知识。学数学，需要毅力。

（四）班级学生程度的参差不齐

一个班级的学生人数是很多的，而每个人都是不一样的个体，自然，对数学的掌握程度就是不同的。男生适应性和创新意识比女生强，而相较于男生，女生则比较细心，细节、条理性、规范性做得比较好。学习习惯好，学习自主性强的学生，会积极思考寻求适合自己的学习方法，那对数学的掌握度必定是高的。那不喜欢思考的学生，习惯照搬照抄，碰到稍微创新的题目，便无从下手，生出退缩之意，对数学知识的思考不够，久而久之，只会越听越懵懂，越学越辛苦。因此，一个班级的学生，即使在一起学习，最后每个人都是会表现出自己的不同之处。

二、解决高一学生学习数学困难的几点做法

（一）激发学生学习兴趣，调动学生学习积极性

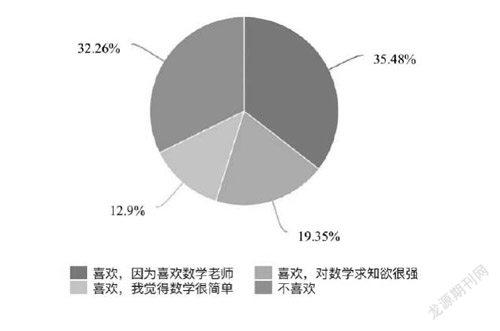
爱因斯坦说过：“兴趣，是最好的教师。”可见兴趣对数学学习的重要性。兴趣是可以靠后天进行培养的，不排除有的学生对数学本身就有很强的求知欲，但大部分的学生对数学的兴趣还是需要后期环境的潜移默化，让他慢慢地体会数学的趣味性。让学生对数学产生兴趣的原因有很多，可以是解出来一道数学题的成就感带来的，也可以是与同桌一起合作数学学习的快乐带来的。关于激发学生对数学学习兴趣的猜想，我做了一个简单的问卷调查，调查结果如图：

通过调查结果，可以尝试两种形式：一是通过教师对学生的关注，进而让学生喜欢学数学;二是从求知欲望方面，来增强学生对数学学习的喜欢。

高一学生处于青春期，叛逆也单纯，教师应当多关注学生，课堂上多提问，下课后多了解学生的学习情况。有的时候，教师在课堂上随口的一个问题就能加强学生对数学学习的信心;课后与学生交谈的某一句话便是他学习数学的动力。是教师，也是朋友，和谐的师生关系，教师更好地做学生数学学习的引路人。

每一个新的知识都有它存在的意义，每个人对新知识都会有好奇心，教师要及时抓住学生对新鲜事物的好奇心，保持住学生对新知识的求知欲。课堂上讲解新知识的时候，可以先提出问题让学生思考[1]，然后，通过学习新知识，来解决提出的问题，这样不仅引发了学生学习数学的兴趣，也让学生对新知识有一定的思考。下面以学习对数的概念为例，可以这样提出问题：

师：若2x=64，则x等于多少？

生：x=6。

师：若2x=1024，则x等于多少？

生：x=10。

师：若2x=3，则x等于多少？

生：虽然我知道有这样的数，但是我写不出这个数。

当学生写不出这个数的时候，正是学生对问题求知欲最强烈的时候，此时，及时地引入对数的概念，告诉学生x可以写成log23，然后再开始对数概念的讲解，这样让学生思考了对数由来的过程，也解答了学生的疑问，日积月累，学生对数学学习的兴趣便能得到提高。

（二）抓基础，重视数学的严谨性与规范性

一个新的知识是需要学生反复揣摩的，只有基础打得牢，后面的学习才能够顺利进行，而数学这门学科既讲究严谨也讲究规范，它贯穿在数学学习的每一个时刻。在平常的教学过程中就应当要对学生反复强调，复习练习。例如：在学习函数奇偶性时，判断一个函数的奇偶性，要做的是，判断函数的定义域，是否关于原点对称。[2]这一点，有很多学生容易遗漏。下面举一个例子：

例1：判断f（x）=x3+2x，x∈[-1，1]的奇偶性。

解：因为函数f（x）=x3+2x，x∈[-1，1]的定义域为[-1，1]，不关于原点对称，所以f（x）为非奇非偶函数。

做判断函数奇偶性的题目时，应该规范学生书写，让学生能够明确，要先判断函数的定义域，是否关于原点对称，如例1所示，即使函数f（x）的解析式能满足f（-x）=-f（x），但是，因为该函数定义域不关于原点对称，所以，就不可能是奇函数或偶函数。

（三）了解学生差异，因材施教

差异不可避免，教师能做的是接受差异，了解差异并根据班级的实际情况因材施教，对我所任教的两个班级而言亦如此，学生差异比较明显，所以在平常的课堂中，要时刻注意学生接受程度的不同，上課多提问不懂的学生，讲解新题型的时候要由易到难，由浅到深。关注学生差异，不仅要从基础讲起，提高题目也要适当地加入课堂中，所以教师教学过程中可以呈阶梯式讲解，例题依次递进，抓住学生的思维，打造高效的课堂环境。比如：在讲解基本不等式的题目时，可以按照例2、例3、例4的顺序给出：

例2：若a，b为正实数，且a+b=2，求ab的最大值。

解：因为a，b为正实数，所以。当且仅当a=b时，等号成立。

因此0

例3：当x≥1时，求的最小值。

解：由x≥1，得x-1>0，

故。

当且仅当，即x=3时，等号成立，因此的最小值为5。

例4：设，求的最大值。

解：由，得2x-1<0，1-2x>0。

故

。

当且仅当，即x=0时，等号成立，因此的最大值是-1。

（四）多总结题型，多训练语言表达

数学学习是模块式的，教材将其分为单元，在每一个单元的学习结束之后，应当及时跟进复习总结，将这一单元中的知识点和题型进行整合，让学生在总结过程中发现问题，查缺补漏。另一方面，高一学生有一个很严重的问题就是语言表达能力不强，有的时候在思路完全正确的情况下，语言表达不清导致逻辑的错误，所以，应当要对学生表述能力进行加强，有针对性地做适当训练。高一学生学习过程中最明显的就是集合中交并集运算过程中的语言描述，容易出现逻辑问题，要让学生多说，多表达，让交并集的逻辑融入学生的思想中。

参考文献

[1]于立平.初中数学教学中高效课堂建设策略研究[J].学周刊，2015.

[2]李毅.解析分段函数提高思维水平[J].数理化解题研究：高中版，2013.

[3]张大均.教育心理学[M].北京：人民教育出版社，1999.

[4]张媚娟.高中数学成绩差的成因及对策[J].今日科苑，2009（16）.

[5]王淑娟.高中生函数学习障碍成因及对策研究[D].广西师范大学，2014.

本文系福建省教育科学“十三五”规划2020年度专项课题“数学核心素养下的高中生数学阅读能力培养的研究”（项目编号：FJJKXB20-1150）研究成果。