基于虚拟样机技术的某商用车操纵稳定性仿真分析研究

周宁，张学萍

（1.安徽职业技术学院 汽车工程学院，安徽 合肥 230011；2.安徽三联学院 机械工程学院，安徽 合肥 230601）

操纵稳定性是衡量汽车主动安全性能的重要因素，其性能的好坏直接影响汽车的安全行驶。评价汽车操纵稳定性的指标往往包括转向盘角阶跃输入下的稳态与瞬态响应、回正性及蛇形试验等一系列核心参数；广大学者为了获取这些评价指标往往采用两种方法，即建立开路系统的客观评价法和建立人-车闭路系统的主观评价法，而这两种研究方法普遍存在周期过长、成本较大的缺点。

本文采用虚拟仿真的方法建立所研究汽车的整车数字化模型，按照具体国标的要求设置仿真条件，展开针对该车的蛇行试验、方向盘角阶跃输入仿真及稳态回转试验等方面的仿真试验研究，为该车的进一步优化设计提供了一定的理论支撑。

1 操纵稳定性理论分析

在汽车操纵稳定性的建模中，通常把整车简化为侧向、横摆两个自由度的两轮汽车模型，两轮汽车模型及车辆坐标系如图1所示；建模过程中忽略转向系统的影响，仅以前轮转角作为输入；假定车辆相对于地面只作简单的平面运动，且其沿x轴的速度不变，侧向加速度限定在0.4g以下，车辆的轮胎侧偏特性处于线性范围［1］。

图1 两轮汽车模型及车辆坐标系

经过计算，建立二自由度的汽车运动微分方程，在此基础上进行稳态响应、瞬态响应的分析，并推导出各个参数的表达式。通常用来描述汽车瞬态响应的参数有横摆角速度ωr波动的固有（圆）频率ω0和反应时间τ［1］。ω0的值越高，代表瞬态响应品质越好横摆角速度ωr波动时的固有（圆）频率ω0：

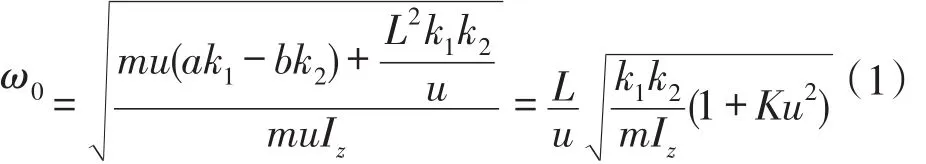
式（1）中，m为整车质量，k1、k2分别为前、后车轮的侧偏刚度，a、b分别为前、后轴到质心的距离，u为横向速度，K为稳定性因数，Iz为转动惯量，L为轴距。

响应时间τ：汽车的横摆角速度在前轮角阶跃输入下，需要经过一个短暂的响应时间τ才能达到稳态值，这个时间也是横摆角速度第一次达到稳定值ω0的时间。

式（2）中，M为整车质量，Φ为角度，Ω为角速度，k1、k2分别为前、后车轮的侧偏刚度，a、b分别为前、后轴到质心的距离，u为横向速度，δ为前轮转角，Ζ为阻尼比。

2 整车模型的建立

根据该商用车的结构及设计图纸，将其主要参数作为在ADAMS/Car中建立整车动力学模型的基础和参考，如表1所示。

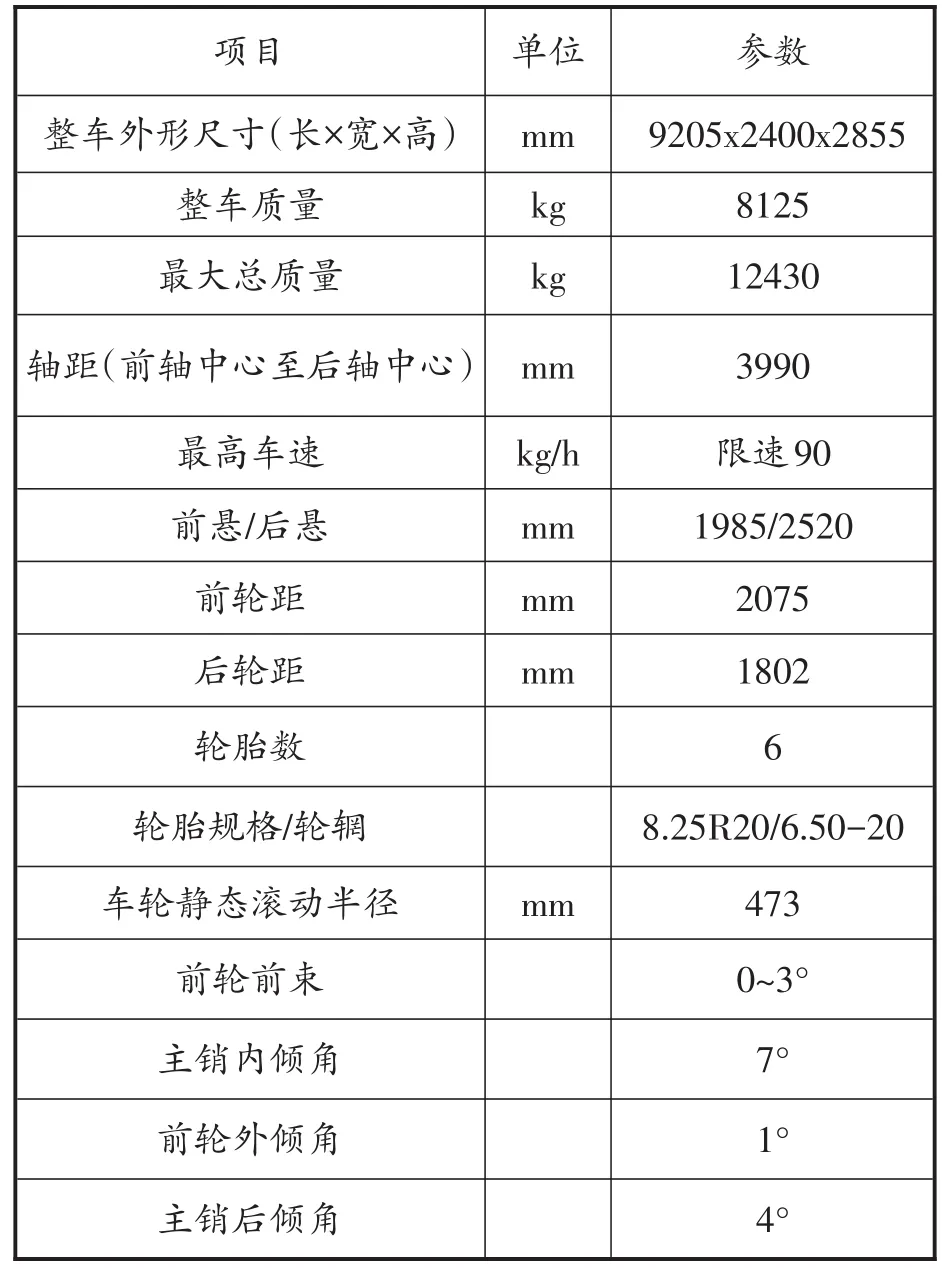
表1 商用车整车主要设计参数

2.1 前后悬架模型的建立

商用车的前后悬架均为非独立悬架，建立符合实车结构特性的前后悬架系统模板。

2.2 转向系统模型

ADAMS软件中包含卡车转向系统的模板，为了建立商用车转向系统模型，在模版基础上对硬点坐标进行了修改，重新赋值系统中部件的质量特性，对转向器传动比进行了修改，编辑转向助力特性［2］，建立转向系统模型。

2.3 轮胎模型

虚拟样机中有Fiala轮胎模型、UA轮胎模型、使用魔术公式Magic-Formula的轮胎模型、柔性环轮胎模型(FTire)共4种轮胎模型。

根据表1整车轮胎相关参数，设置轮胎模型相关参数，调用系统中的UA轮胎模型，建立的前后轮胎模型。

2.4 动力系统模型

ADAMS所提供的动力系统模板中提供了发动机、离合器、变速器和差速器分总成功能。文中所用的动力系统模型是参照软件中的模板建立，建立的动力系统动力学模型。

2.5 整车系统模型

在Adams/car模块标准界面中，对上面步骤中建立的各子系统进行装配，隐去车身后的整车模型结果如图2所示。

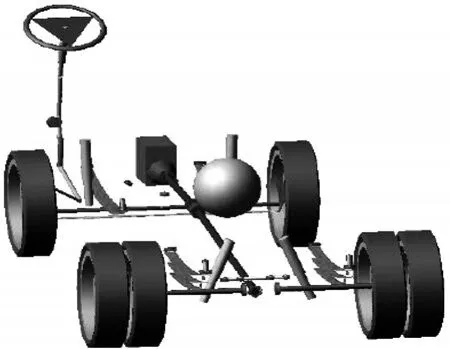
图2 Adams/Car中整车模型

3 操纵稳定性仿真分析

根据国标GB/T6323.2-94的规定，本文对该商用车的操纵稳定性进行转向盘转角阶跃输入仿真、转向回正仿真和蛇形仿真三项实验。

3.1 转向盘转角阶跃输入仿真

3.1.1 试验方法

根据国标GB/T6323.2-94中规定的试验方法，结合文中商用车的实际情况，此次仿真设定在满载的状态下进行，并且只进行一次向左转。在本次实验过程中，车辆的行驶速度为90km/h，当直线行驶到2秒时，在0.2秒的短暂时间内，以极快的速度，将方向盘转角从0°调整为50°，之后方向盘转角保持在50°固定不动，直到车辆再次达到稳态，稳态侧向加速度达到2m/s2。

3.1.2 仿真结果分析

本商用车按照上述试验方法进行仿真，横摆角速度、侧向加速度与时间的关系曲线如图3、图4所示。

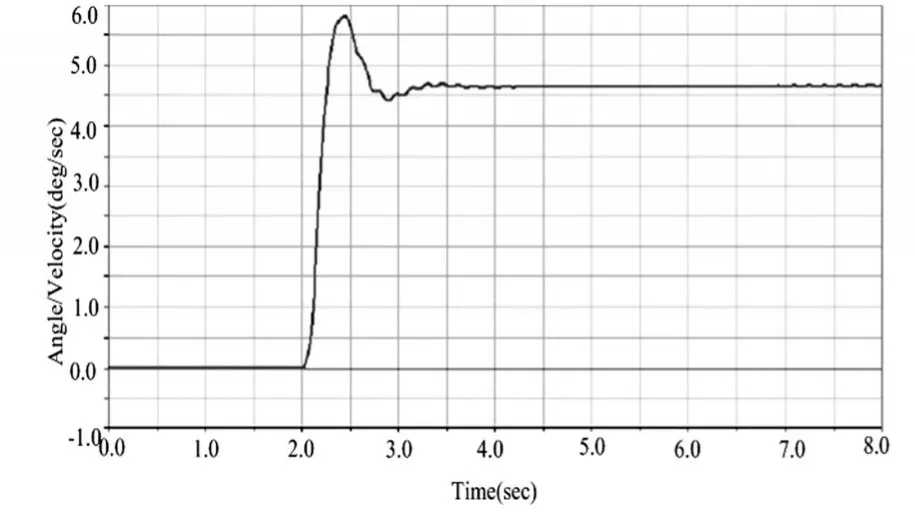
图3 角阶跃转向下的横摆角速度

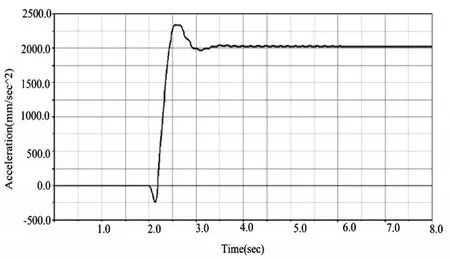
图4 角阶跃转向下的侧向加速度

响应时间的长短直接影响车辆的瞬态响应性能，即响应时间越短，代表车辆瞬态响应性能越好，反之则越差。从图3可以看出，该商用车的横摆角速度响应时间为1.5s，其反应时间较短，表明其车辆瞬态响应性能较好。从图4可以看出，该商用车方向盘转角在50°时，侧向加速度达到峰值所用的时间为0.5s，响应时间较短，并且经过1.0s后，该商用车的侧向加速度即趋于稳定，整个过程中，响应时间较短，说明此商用车的侧向加速度瞬态稳定性较好。

3.2 转向回正仿真试验

3.2.1 试验方法

根据国标GB/T6323.4-94规定，结合该商用车的具体情况，对其进行低速回正和高速回正两个仿真试验。本试验在满载状态下进行，仿真只按向左转方向进行一次。

3.2.2 仿真结果分析

本商用车横摆角速度、侧向加速度与时间的仿真关系曲线如图5、图6所示（图5、图6中，低速回正实线表示，高速回正虚线表示）。

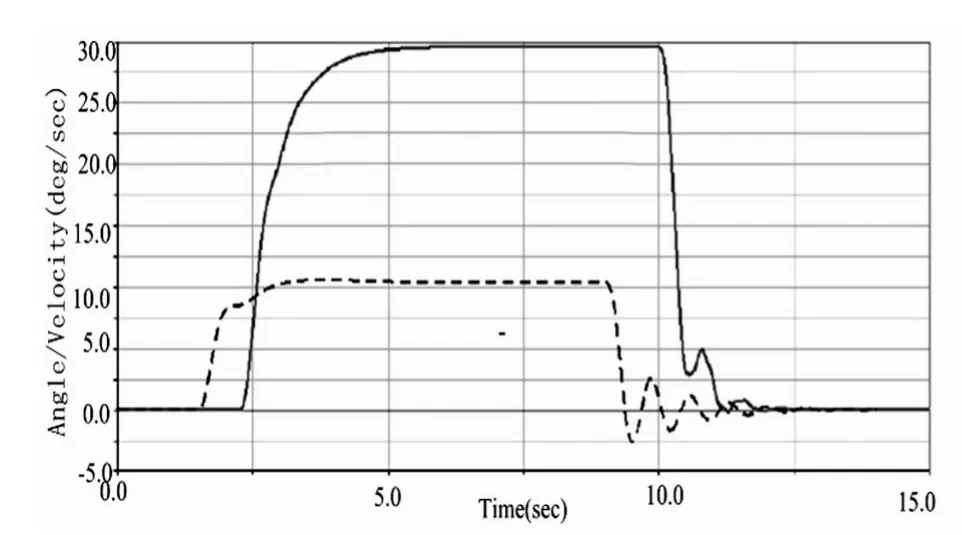
图5 转向回正下的横摆角速度

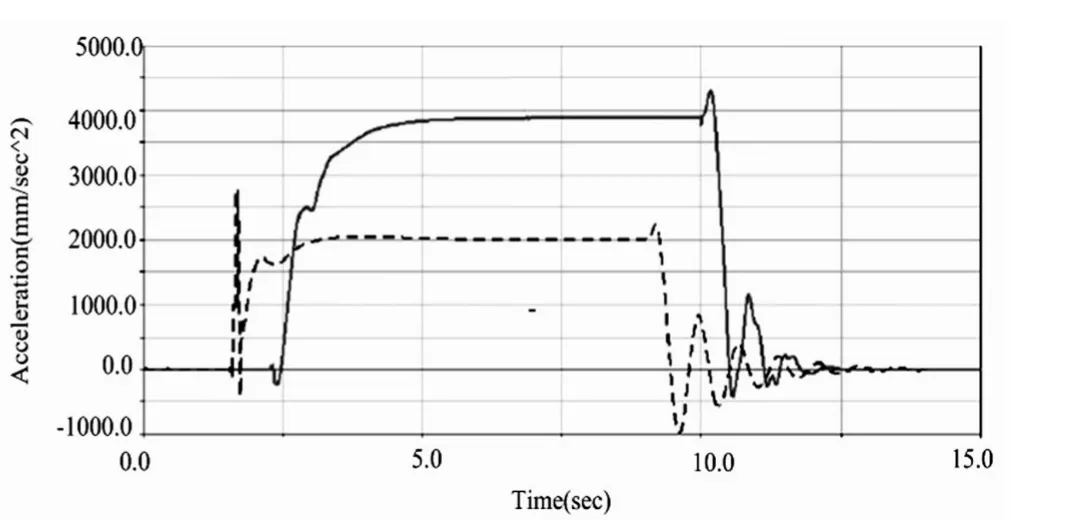
图6 转向回正下的侧向加速度

从图5、图6分析可知，在松开方向盘后，该商用车的横摆角速度和侧向加速度对应的均进行波形的振动，且低速和高速回正两种类型的振幅都不断在变小，经过10s左右的震荡后，波形进入到一个稳定状态。在整个变化过程中，低速回正表现出来的角度比高速回正的振幅均大，符合国标规定的回正试验要求。同时，也说明该车由曲线自行恢复到直线行驶的能力强，回正性能良好。

3.3 蛇行仿真试验

3.3.1 试验方法

根据国标GB/T6323.1-94的规定，设定蛇形实验在汽车处于满载状态下进行，标桩间距设定为30m，该车分别以32.5km/h、40km/h、50km/h三种稳定车速进行直线行驶进入试验路段。首先记录各测量变量的零线，然后该车蛇行通过试验路段，在这个过程中记录各测量变量的时间历程曲线和通过有效标桩区的时间［3］。

3.3.2 仿真结果分析

本商用车按照上述试验方法进行仿真，横摆角速度、侧向加速度、质心侧偏角以及汽车运动轨迹（图7-图10中，粗实线代表车速为32.5km/h、粗虚线代表车速为40km/h、细虚线代表车速为50km/h）。

从图7-图9可知，横摆角速度峰值、侧向加速度峰值、质心侧偏角峰值与车速变化成正比，随着该商用车车速的增加，三个参数的峰值增大，通过标杆时间缩短。

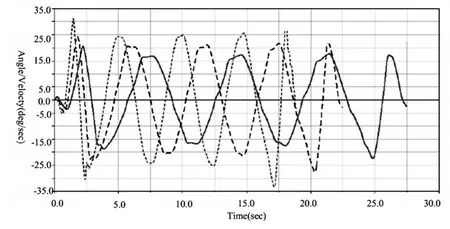
图7 不同车速下的横摆角速度

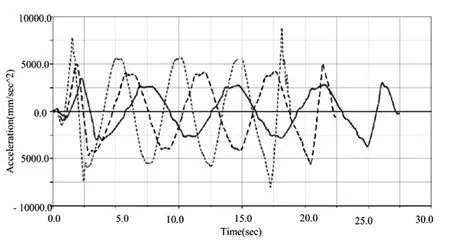
图8 不同车速下的侧向加速度图

图9 不同车速下的质心侧偏角

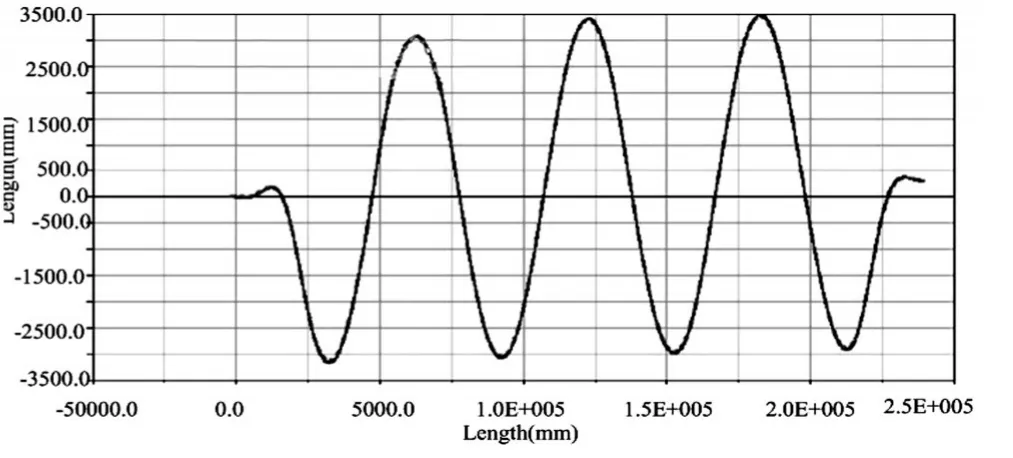
图10 不同车速下的汽车运动轨迹

从图10可以看出，车辆在进行蛇形试验时，三种车速运动轨迹重合，在运动过程中，车辆可以较好的按照设计标杆行驶。结合蛇形试验的目标可知，说明该商用车追随性能良好。

4 结论

本文基于虚拟样机技术，运用Adams/Car模块建立整车模型，根据国标要求进行转向盘转角阶跃输入试验、稳态回转试验和蛇行试验，得到横摆角速度、侧向加速度及质心偏转角等参数随时间变化的仿真曲线。通过对仿真参数结果与国标进行对比分析，该商用车的操纵稳定性仿真试验符合要求，结果对汽车操纵稳定性的评价具有一定的指导意义，为转向系统的设计提供思路和借鉴。