基于知识图谱的模糊推理与应用研究

倪政林

（马鞍山职业技术学院 电子信息系，安徽 马鞍山 243031）

随着移动互联技术的快速发展，网络信息呈指数级、爆炸式增长［1］-［3］。网络信息日益超载及数据异构性增加，导致利用遗传算法、协同过滤、关联挖掘、K-均值聚类算法、神经网络、遗传算法、深度学习或蚁群算法等技术进行知识挖掘的效率受到严重的影响。2012年，谷哥公司提出知识图谱（Knowledge Graph）的概念并实现了更智能的搜索引擎，大幅提高了知识搜索的效率，引起学术界和工程界的普遍关注。之后，知识图谱在机器人聊天、大数据挖掘与风险管控、证券投资及数据分析、智能医疗专家系统等领域有着广泛的研究与应用。

现有的知识图谱主要利用图结构及资源描述框架（Resource Description Framework）中的描述逻辑（Description Logic，）规则进行确定性推理获取知识［4］—［5］，缺乏鲁棒性和包容性，致使知识的查全率受到影响。在某些如教育、艺术文化等领域，信息、资源具备多元化、异构性特点，不属于非真即假的二元逻辑，知识的查全率会更低。针对这一不足，在知识图谱的推理中引入模糊理论，通过补充模糊推理实现更高的知识查全率。

1 相关理论

1.1 知识图谱

知识图谱通过利用知识工程、图形学、信息可视化技术等相关技术；采用本体（Ontology）理论对知识进行形式化规范定义；使用万维网联盟（W3C）的资源描述框架规范建立多维知识结构图。知识图谱形式化定义为：G={E，R，S}，其中：E为实体、R为实体间的关系、S为实体集［6］。知识图谱是一个由实体及实体间联系、实体及属性间联系组成的多边关系图，关系图中的结点为实体或属性、边为不同实体或实体属性间的关系。知识推理方法主要基于描述逻辑推理、基于图结构推理、基于知识图谱向量表示学习推理等。

1.2 模糊理论

Zadeh（扎德）于1965年首次提出模糊集，之后模糊论得到广泛的研究与应用。模糊理论指利用模糊集合或隶属度函数对事物、信息、过程等进行分类、管理、控制及推理的理论。模糊论广泛应用于工业自动控制、军事、医疗专家系统及人工智能等领域。模糊推理主要包含模糊判断句的集合表示与逻辑运算、同一论域上的模糊逻辑推理句与推理规则、不同论域上的模糊推逻辑理句与推理规则、似然推理与条件推理等。其中，条件语推理包含简单分支条件、多分支条件、复合蕴涵（多条件组合）模糊推理［7］等。

2 知识图谱模糊推理

2.1 知识判断模糊集与逻辑运算

设X为知识图谱中的知识判断论域，(j)是X上的一个模糊判断句，则X的模糊子集J(x)定义为式（1），即：

其中，J为(j)的集合表示；T［j(x)］∊［0，1］，表示(j)对x 的真值或依赖程度。若(j)(x)＞0.5，则(j)对x为模糊真（）；若(j)(x)≤0.5，则(j)对x为模糊假（）；若∀x∊X且(j)(x)＞0.5，则(j)为模糊真（）；若∀x∊X且(j)(x)≤0.5，则(j)为模糊假（）。

设X为知识图谱中的知识判断论域，(j)、(k)是X上的模糊判断句，则(j)、(k)的逻辑与、或、非运算分别定义为式（2）、式（3）、式（4）：

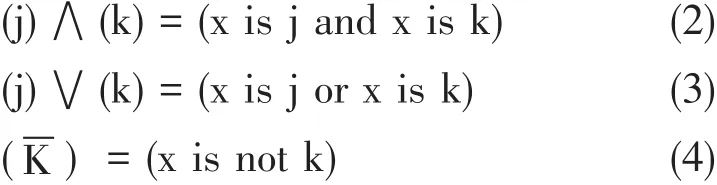
设J为(j)集合、K为(k)集合，则逻辑运算 (j)⋀(k)、(j)⋁ (k)、()的集合运算分别表示为：J⋂K、J⋃K、KC。

2.2 模糊推理规则

（1）同一论域上的推理

设X为知识图谱中的同一知识判断论域，(j)、(k)是X上的模糊判断句，若(x is j)则(x is k)，记为“(j)→(k)”。肯定前件的假言推理、否定后件的假言推理、合成推理规则分别定义为式（5）、式（6）、式（7）：

（2）不同论域上的推理

若(x is j)则(y is k)，记为“(j(x))→(k(y))”，(j)的真域J⊆X，(k)的真域K⊆Y。不同论域上模糊推理真域为R=（J×K）⋃ (JC×Y)，其隶属函数R(x，y)=(J(x)⋀ K(y))⋁ (1-J(x))，其中R(x，y)为推理句(j(x))→(k(y))对(x，y)的真值（）。不同论域上的推理规则同本节第1点类似（从略）。

（3）似然推理与条件推理

似然推理是一种变换推理，其定义为：设R是(j(x))→(k(y))的真域，则R∈F(X×Y)，R为从X到Y的模糊（F）变换关系，R：F(X)→F(Y)，J′｜→K′=J′○R，其中K′(y)=(J′○R)(y)=Vx∈X(J′(x)⋀R(x，y))， ○为F变换关系的合成运算。

简单分支条件推理描述为“IF(j)THEN(k)ELSE(l)”，其真域R=（J×K）⋃（JC×L），隶属函数为：R(x，y)=(J(x)⋀ K(y))⋁ (1-J(x)⋀L(y))，若推理规则为J′，则似然推理结果为：K′=J′○R。

多分支条件推理描述为“IF(j1)THEN(k1)ELSE IF(j2)THEN(k2)ELSE …”，其真域 R=（J1×K1）⋃（J2×K2）⋃…⋃(Jn×Kn)，隶属函数为：R(x，y)=Vni=1（Ji（x）⋀K（y））。

多条件组合推理描述为“IF (j1)and(k1)THEN(l1)”，其真域R=J1×K1×L1，隶属函数为：R(x，y，z)=J1(x)⋀K1(y)⋀L1(z)。

2.3 推理过程

知识图谱中依据图结点类型进行的推理过程可分为横向推理、纵向推理和混合推理三种。即：（1）横向推理。由一个或多个实体结点推理出新实体知识的过程为横向推理。条件横向推理过程分为简单分支推理过程、多分支推理过程、多条件组合推理过程。其它横向推理过程与条件横向推理类似。（2）纵向推理。如果把横向推理看作在一维平面中进行推理与搜索，纵向推理则是向多维空间中推理与搜索。由一个或多个实体推理出新的实例或属性的知识推理过程为纵向推理。（3）混合推理。混合推理过程指既有横向推理又有纵向推理。混合推理过程如图1所示，其中本体（E）层内进行横向实体推理，本体→实例（I）→属性（A）或本体→属性进行纵向推理，虚线箭头表示为似然推理。

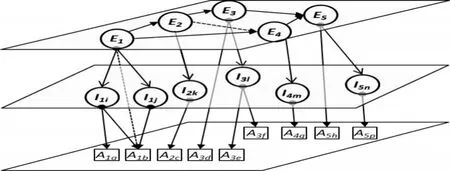
图1 混合推理过程

3 应用研究

3.1 环境搭建

3.1.1 在线课程资源知识图谱构建

在线课程资源主要包括课程实体(c)及资源实体(rs)，其中c=（课程名，包含/具有，实例/属性）、rs=（资源名，具有，类型）。在线课程资源元信息主要包含：课程大纲（CB）、学习目标（TO）、课件（CW）、直播或录播视频（L|R）、动画（AM）、微课（MC）、案例（CS）、素材库（ML）、试题集（TS）、名词术语（TL）、常见问题解答（FQ）、在线讨论及记录（OD）、模拟平台或共享软件（P|S）、参与资源或扩展学习网址（R|E）。课程本体包含若干课程实体（ci），一个ci又包含若干课程实例（cij），每一cij具有若干类型资源，资源本体包含若干资源实体（rsk），每个rsk具有若干类型资源。

在线课程资源知识图谱构建过程主要分四步：数据获取、信息抽取、知识表达与融合、知识获取。构建知识图谱的技术模型如图2所示，其中知识获取的推理结合了确定性推理与模糊推理。

3.1.2 个性化特征模型及数据挖掘

（1）特征模型

个性化特征主要包含知识背景或学习基础、能力、兴趣、在线学习时间分配等要素。个性特征模型向量定义如式（8）所示，其中：xi为第i位学习者实例，各分量分别为基础背景（）、学习能力（）、兴趣特征（）、学习时间分配特征（），μi、νi、οi、λi为各分量系数；gij为成绩，cij为学分，pij为绩点，ai1-ai4分别为注意力、记忆力、理解创建力、语言表达力，兴趣ni1-ni4分别为文本、视频、练习、讨论，ti1-ti3分别为平均学习时长、学习时间日分布、学习时间周分布。

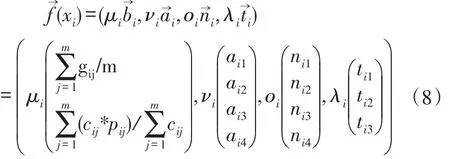
（2）数据计算与挖掘

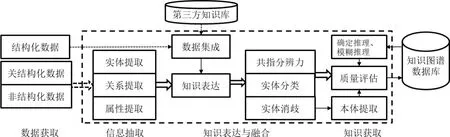
图2 知识图谱构建技术模型

包含了均分及平均总绩点分量，各分量值的计算如式（8）中第一列所示。ai1-ai4各项能力值评估见式（9），其中：k=1～4、avgik为个人均值、normalik为一般均值。、中各分量值通过对浏览内容、浏览时间等数值的协同过滤挖掘与评估获得［8］。

3.2 个性化知识查询

3.2.1 个性特征值单位化处理与模糊判定推理

个性学习特征不是绝对的，随着学习环境、个人成长及努力程度会不断变化。针对特征模型挖掘出的各特征值先进行单位化数据处理，即：若是数值型则通过数学方法缩放至［0，1］；若是非数值型如时间日分布和周分布则通过二项概率分布函数，如式（10）所示，建立概率分布值。对各分量值进行模糊化处理，建立个性化特征值模糊集，再通过模糊判定推理建立个性特征库。

3.2.2 知识查询过程

第一步：生成课程实体及所有实例资源树。

依据个性化查询需求，从知识图谱中通过混合模糊推理过程抽取出相关课程实体及其前导与后续课程实例集，以及各实例包含的资源集，然后生成资源树。

第二步：剪枝与防过渡剪枝。

第三步：生成个性化资源树。

经过第二步剪枝后，如果有多实例、前导或后续，则分别合并成一个实例、前导或后续；如果某个实例、前导或后续结点含有多个同类资源则只保留质量或评价最优的叶子结点；保留所有不重复的资源结点，最后生成的个性化查询资源树。

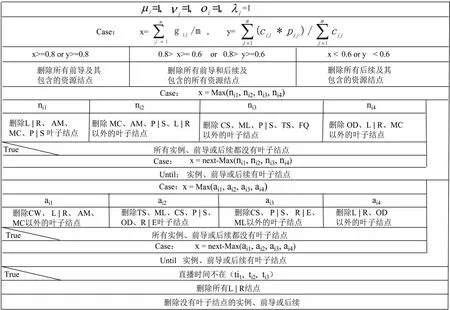
图3 剪枝算法

4 实验结果与分析

为了验证查全率，设计了对比仿真实验。实验环境为：Intel Core i5-8500、主频 4GHz、内存12GB、操作系统64位 Windows 10、语言为Py⁃thon3.7和Cypher、数据库管理系统为Neo4j。

首先设计了一个工商管理专业的知识图谱，其中包含35门课程及437个不同种类学习资源，35门课程中包含了同类不完全同名的课程17门，这些课程间具有前导和后续联系。然后分别输入“管理基础”“市场营销”“会计基础”“营销心理学”进行确定性与模糊推理查询，其结果如图4所示。

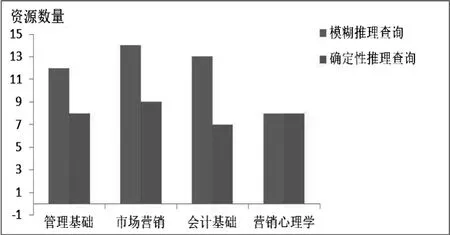
图4 两种推理查询结果对比

从图4可知，管理基础、市场营销、会计基础课程的资源数量在两种推理查询下结果不同，这与模糊推理的应用有关，提高了查全率；营销心理学的课程资源量查询结果一样，由于设计实验的时候没有对这门课增加不同名课程，这表明在没有多样化实例背景下，模糊查询与确定性查询的查全率没有变化。

5 结论

本文在介绍知识图谱及模糊理论之后，将模糊推理技术引入知识图谱的知识推理中，重点研究了知识判断模糊集与逻辑运算、模糊推理规则及推理过程，并以网络课程学习资源为例，较详细介绍了课程资源知识图谱的构建、个性化特征模型与特征挖掘、个性化知识推理查询及剪枝与防过度剪枝的算法设计，最后通过仿真实验验证了模糊推理技术在多元化知识图谱中进行知识查询对查全率的提高是有贡献作用。尽管如此，但基于知识图谱的模糊推理完备性还有待进一步的证明，即在多元异构的网络环境中如何评价和归并碎片的学习资源、如何在学生信息大数据背景下提高个性化特征挖掘的准确性是面临的主要挑战。未来，对知识图谱的模糊推理完备性、引入深度学习等人工智能技术对资源识别及学生的个性化特征挖掘等作进一步深入的研究。