基于过程化考核的学习过程数据关联分析研究
赵祥好,朱方洲
(安徽省委党校 信息技术中心,安徽 合肥 230022)
基于过程化管理的教学模式成为当前教学改革的热点[1],我国随之出台了一系列关于加强学习过程管理及学习过程考核的举措,健全了能力与知识考核相结合多元化的学业考核评价体系,进一步完善了学生的学习过程中的监测、评估及反馈机制。许彧青、程巧娟等[2]提出了针对选题阶段、开题阶段、设计进行阶段、设计完成阶段、答辩阶段和答辩后六个阶段的过程化考核体系;熊宗杨、薛学斌等[3]构建了基于过程化考核的在线考试的系统,通过成绩统计,试卷分析及教学建议等功能进行综合分析评估;陈昕[4]提出了阶梯式递进的“编程”考核方式;彭绪山[5]则利用问卷调查及实践实验的方法进行过程考核。
“新时代高教40条”提倡多样化、过程化考核,要求课程成绩不能简单地以期末考试为准,应改变传统的考核方式,加强学生的学习过程考核。基于此,本文提出了一种基于过程化考核的学生学习过程数据关联分析方法,采用自主研发的智慧教学辅助系统采集学习过程数据,并在教学实践中证明该方法的有效性。
1 关联规则的概述
1.1 关联规则的概念
设I={i1,i2,…,im}是项的集合,i是项集I中的任意一个项,事务集用D表示,是进行关联规则挖掘的所有数据的集合,而T表示事务集中的每一个事务,它也是项集,由一个或者多个项i构成,同时使得T⊆ I。
关联规则通常表示为从“X→Y”的形式,X表示关联规则左侧的项集,是关联规则中的先决条件,Y表示对应的关联结果是右侧项集,同时说明了数据内隐含的关联性。
支持度是指在所有的关联规则的项集中,{X,Y}是成对出现的可能性,也就是指在项集中X和Y同时出现的概率,即:
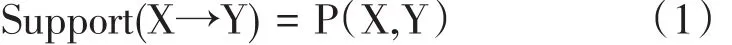
支持度很好地衡量了当前所考察对象关联规则在“量”上的大小,也就是通过设定最小的阈值,保留出现比较频繁的项集所隐含的规则,从而剔除出现频率较小的规则。即:
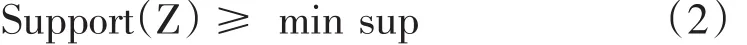
其中min sup表示为最小的支持度,所有满足式(2)的项集Z,都称为频繁项集。
置信度则表示在关联前件X发生的前提下,关联后件Y所发生的概率,即:
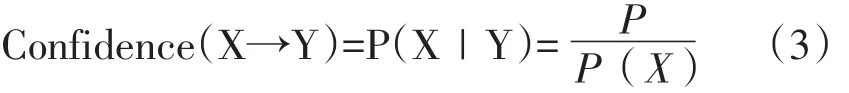
式(3)衡量了所考察对象在关联规则“质”上的可靠性。并通过支持度进行筛选出频繁的项集后,再进一步来设定置信度的最小阈值做最终筛选,从而生成满足条件的强关联规则,即:
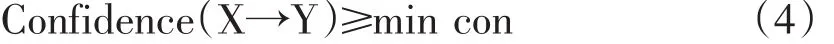
式(4)中,mincon表示为最小的支持度。
1.2 Apriori算法的思想
Apriori算法是指首先要列出所有项的集,再通过计算项集的支持度进行筛选,保留所有大于或等于min sup的项集;最后由上一步中所找到的规则,使用连接步方法生成下一步项集,再通过剪枝步思想利用Apriori算法的性质产生候选项集,剔除出不满足条件的候选项集。这样逐层迭代,一直到所产生的项集集合全部为空集,算法才终止,列出所有频繁项集。
2 基于关联规则的学习过程数据的分析
2.1 方案设计
本文以《网络工程管理》课程教学为例,该课程的过程考核指标分配如下:出勤率为10%,课后作业为10%,课堂测验为20%,期中考试和期末考试各为30%。在教学过程中,可进行多次课堂测验,以便检查学生对课堂新知识的掌握情况;教学任务结束后,采用闭卷的方式进行期末考试。基于卷面成绩基本上能反应出学生对知识点的掌握情况,以此作为检验其他各项在过程化考核中数据的主要指标。鉴于出勤率和课后作业均是手工统计数据,准确性无法保证,本文不做进一步研究,本文重点对数据采集比较准确可信的课堂测验、期中和期末成绩三个维度进行研究。在样本中选择以上三个维度数据,导出数据源类型为Ex⁃cel工作表,并采用 Apriori算法、IBM SPSS Model⁃er 18.0挖掘工具,挖掘学生在过程化考核中数据之间的关联性,即找出学生平时课堂测验、以及期中考试成绩与期末考试成绩三者之间的关联关系。
2.2 数据准备
文章选取某高校2017级网络工程专业的3个教学班级,共计78名学生的《网络工程管理》课程教学过程化数据为研究对象。数据分为课堂测验、期中考试及期末考试三个维度,其中课堂测验和期中考试数据均通过自主开发的课堂教学辅助系统收集,数据真实可靠。
由于原始数据中有异常数据存在,剔除掉6个无效的数据以后,有效的样本量为72个。每个样本点包括学号、姓名、专业、班级、课堂测验、期中考试和期末考试等字段,进一步对数据进行处理,生成包含学号、课堂测验、期中考试、期末考试这4个字段的学习过程考核数据表,其记录共有72条,随机选择其中10条记录,如表1所示。
另外,由于Apriori算法仅支持布尔型数据的关联分析,需要将原始的连续数据通过聚类的方式转换成离散型数据。在此步骤中需要运用到K-means聚类算法对表1数据进行聚类。为获取最佳实验效果,在对数据进行聚类离散化处理后,进一步通过手肘[6]找到最佳的聚类K值。
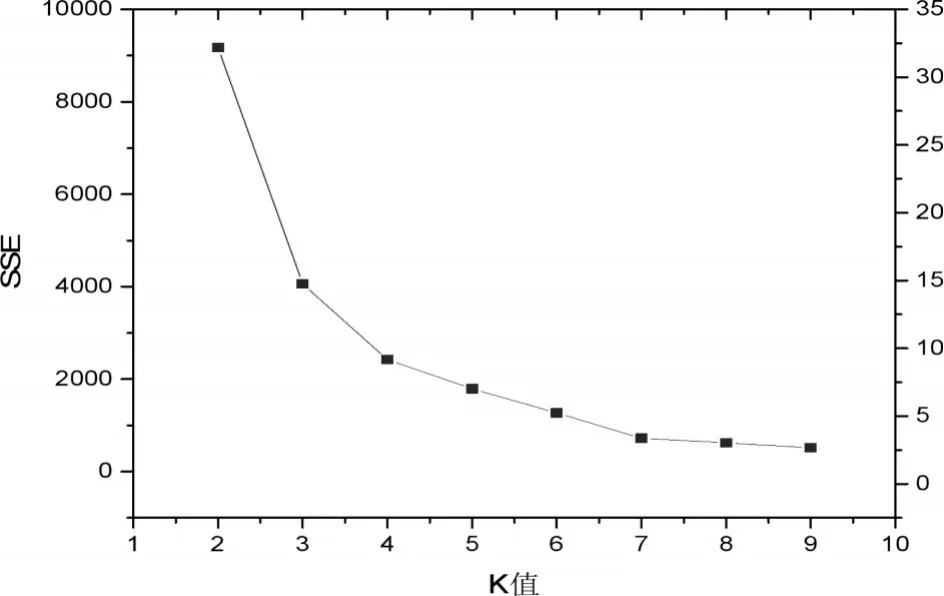
图1 手肘法确定期末成绩分类最佳K值
手肘法是通过SSE和K值之间的关系图确认最优的K值,最优的K值称为“肘部”[7]。
本文以学生的期末考试数据为例,画出误差平方和SSE与K值的关系图,如图1所示,可以找出“手肘”对应的拐点,这时横坐标即为最佳的K值。从图1中可以看出期末考试中的最佳聚类K的值为3。
经过K-means聚类算法进行离散化并采用手肘法得出最佳的K值后,期中测试得分从高到底被依次分为QZ-1、QZ-2、QZ-3和QZ-4四类,课堂测验的正确率从高到低分布,依次分为KT-1、KT-2和KT-3三类,期末考试得分从高到底依次分为QM-1、QM-2和QM-3三类,对表1中的数据进行聚类,就得到聚类结果如表2所示。
经过数据离散化并且确认出最佳聚类K值后,聚类对应的分数及准确率区间如表3所示。
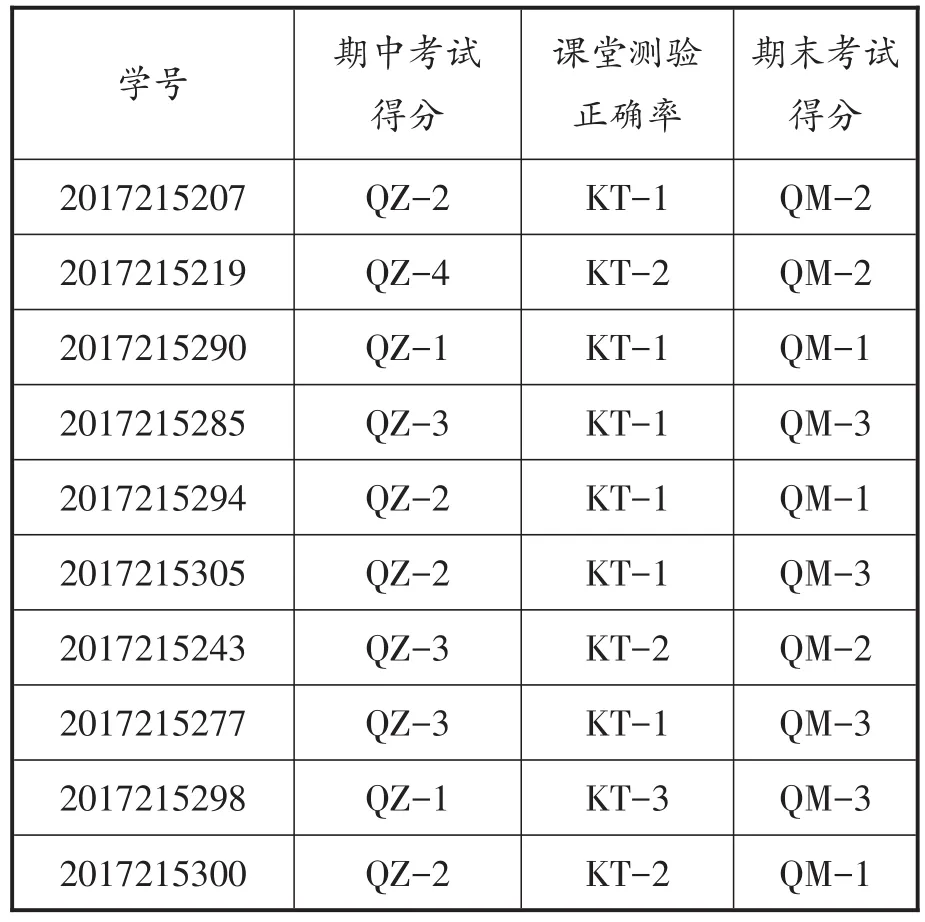
表2 学习过程考核数据聚类
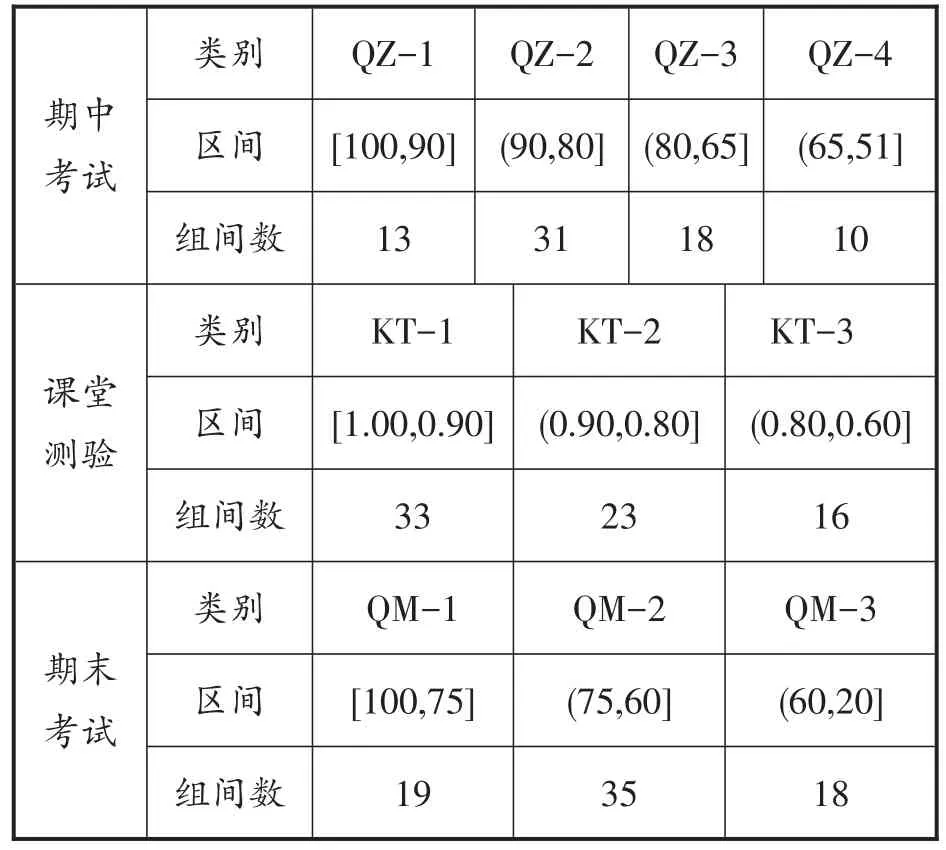
表3 过程考核聚类类别及区间
2.3 模型建立
利用IBM SPSS Modeler 18.0挖掘工具,再采用Apriori算法建立关联分析模型,如图2所示。
通过Apriori算法对期中考试、课堂测验及期末考试三个字段两两建立关联模型,分别得到三者之间的关联规则。期中考试与课堂测验之间的规则如表4所示。以表4中的规则1为例,对挖掘出的关联规则进行分析。
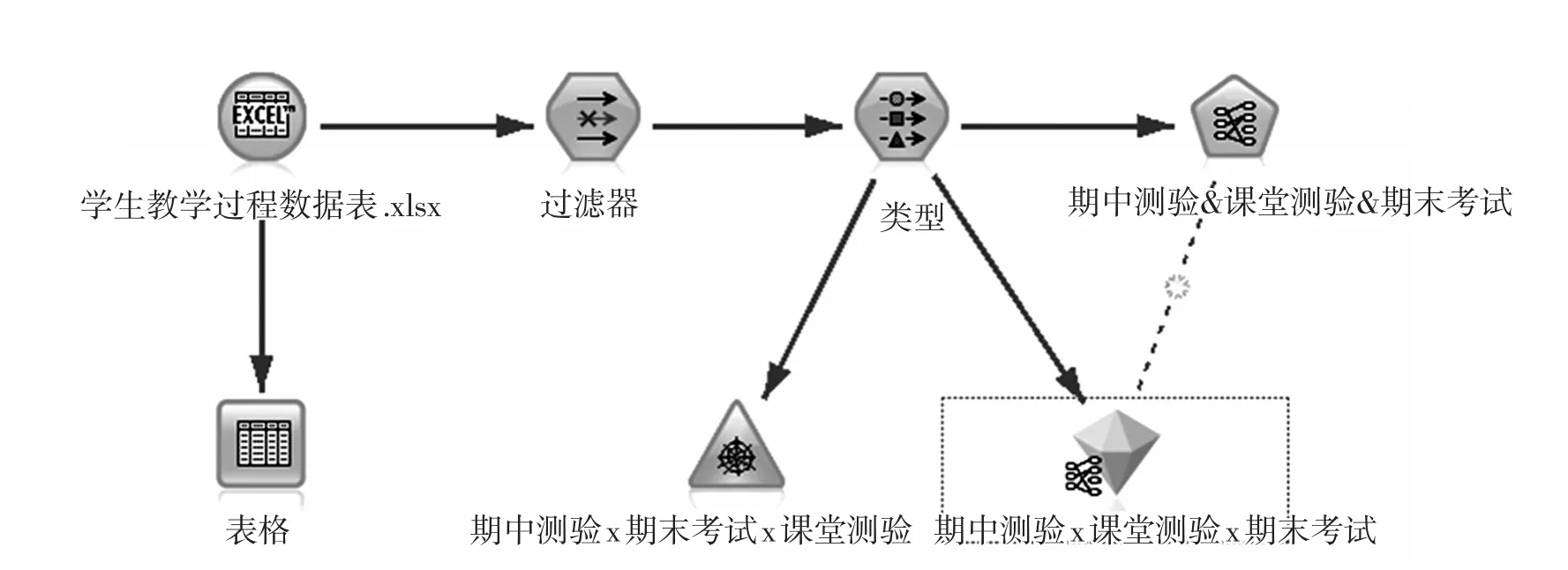
图2 Apriori关联规则算法挖掘模型
规则1为在期中考试成绩为最高分数段QZ-1时,课堂测验正确率类别为KT-1的学习情况相互关联情况。此规则的置信度的值为62.40%,支持度的值为20.58%,说明当学生期中考试成绩较高时,有62.40%的可能性学生在课堂测验的答题中正确率较高,同时期中考试成绩较好在最高分数段QZ-1和课堂测验正确率最高数据段KT-1的概率是20.58%,该规则与经验基本相一致,说明学生在平时的课堂学习中以认真的态度对待教师教授的内容,有助于学生在期中考试中获得优良的成绩。

表4 期中考试与课堂测验之间的关联规则
表5为期中考试与期末考试之间的关联规则。以规则1为例进行说明,在期中考试成绩类别为QZ-2时,对应的学生在期末考试中能够获得最高分数类别的成绩,该规则的置信度为52.15%,即期中测试成绩为中等或者中等偏上学生,有超过50.0%的可能性在期末考试中获得优良成绩,说明学生期中考试成绩的好坏,在某种程度上会直接影响学生期末考试的表现。

表5 期中考试与期末考试之间的关联规则
表6为课堂测验成绩与期末考试成绩之间的关联性。以规则1为例进行分析,在期末考试成绩在最高分数段区间,课堂测验准确率类别为KT-1。这条规则的置信度的值为70.28%,支持度的值为31.29%,说明当学生的期末考试成绩处于较高的分数段时,有70.28%的可能性在课堂测验中表现优良。该规则与教学经验相符,说明课堂学习过程考核数据与期末考试成绩呈现强关联性,说明学习过程化考核对教学质量提升大有帮助。

表6 课堂测验与期末考试之间的关联规则
3 结论
在大数据信息时代下,基于过程化考核的学生学习过程数据关联分析的方法体现出教学考核准确、及时、高效等优越性,解决了教学过程中成绩考核难的问题,提高了学习者的学习水平,促进了高等院校的教学考核工作得到有序开展,为高等院校的教学考核指明了前进的方向。

