双圈图边幻和全标号

邵淑宏，李敬文，顾彦波，王笔美

(兰州交通大学电子与信息工程学院，兰州 730070)

图论以图为研究对象，在图中用点表示对象，两点之间的连线表示对象之间的某种特定的关系.图论在自然科学、社会科学等各领域都有广泛的应用.图的标号问题是图论的研究方向之一.Kotzig和Rosa[1]在1970年首次提出了图的边幻和全标号的概念.目前，国内外关于图优美标号的结果已有很多[2-5]，这些结果为图的边幻和标号的后续发展奠定了基础.1998年Enomoto[6]证明了当n为奇数时，所有的Cn均为超边幻和图，当m=1或n=1时，Km ，n为超边幻和图，当n≠3(mod4)时，Wn为边幻和图；Tn、Pn、sun、Kn、Km ，n、Cm×Cn均为边幻和图[7-8]；文献[9-11]证明了当n≥3时所有的Cn均为边幻和图；Lin[12]等人在2002年给出了部分Fn、友谊图的边幻和标号；Wijaya[13]证明了n为奇数且n≥3时，Pm×Cn为边幻和图；文献[14]证明了当m，n满足一定条件时，Cm∪Cn图为超边幻和图.针对特殊图的边幻和性，Gallian[15]总结归纳了现有的所有标号种类及研究结果，并给出了相应的证明.

本文主要研究利用算法得到有限点内所有图的边幻和全标号，然后从结果集中分析所有双圈图与星图组合联图的标号规律，总结为若干定理并给出证明.

1 基础知识

本文所研究的图均为无向简单连通图，对于图G(p，q)，当q=p+1时，称G为双圈图.文中的星图Sm定义为有m-1个叶子节点和1个中心节点v1.

定义1[6-7]设f为简单无向图G(p，q)从V(G)∪E(G)→{1，2，…，p+q}的一个双射函数.若f满足以下条件：对于图G所有的边uv∈E(G)，点uv∈V(G)，都有f(u)+f(v)+f(uv)=k，k为边幻和常数，则f是图G的边幻和标号(edge-magic total labelling)，简称EMTL，图G是边幻和图(edge-magic graph).若图G的顶点标号满足：f(V(G))→{1，2，…，p}，则f是图G的超级边幻和标号(super edge-magic total labelling)，简称SEMTL，图G是超级边幻和图(super edge-magic graph).

定义2将圈图Cn和Cl任意一顶点并接，设并接点为u1/w1，再将并接点u1/w1和星Sm中心节点v1邻接得到的联图，记为CnΔClSm，V(CnΔClSm)=V(Cn)∪V(Cl)∪V(Sm)v，即|V(CnΔClSm)|=|V(Cn)|+|V(Cl)|+|V(Sm)|-1，E(CnΔClSm)=E(Cn)∪E(Cl)∪E(Sm)∪(u1/w1)v1，即|E(CnΔClSm)|=|E(Cn)|+|E(Cl)|+|E(Sm)|+1.

示例如图1(a).

定义3将圈图Cn和Cl任意一顶点并接，设并接点为u1/w1，再将并接点u1/w1和星Sm中心节点v1并接得到的联图，记为CnΔClΔSm，V(CnΔClΔSm)=V(Cn)∪V(Cl)∪V(Sm)2v，即|V(CnΔClΔSm)|=|V(Cn)|+|V(Cl)|+|V(Sm)|-2，E(CnΔClΔSm)=E(Cn)∪E(Cl)∪E(Sm).

示例如图1(b).

定义4对于双圈图G(p，q)，设图中任意相邻顶点u，v及其边w的标号组成三元组(u，v，w)，存在正整数k(k的取值范围为：p+q+3≤k≤2(p+q))，使得u+v+w=k成立，其中u，v，w∈[1，p+q]，并且u，v，w取值各不相同，则称三元组(u，v，w)的取值空间为双圈图G(p，q)的EMTL解空间，记为δ(p，q，k).如表1所示.

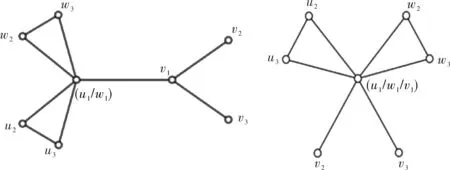
(a)C3ΔC3S3 (b)C3ΔC3ΔS3图1 C3ΔC3S3和C3ΔC3ΔS3Fig.1 C3ΔC3S3and C3ΔC3ΔS3

表1 k-EMTL解空间δ(p，q，k)Tab.1 The solution space δ(p，q，k) for k-EMTL

由定义1和定义2，以下引理显然成立．

引理1如果(p，q)图存在EMTL，则解空间δ(p，q，k)中一定存在满足EMTL的相邻点u，v和边标号w的三元组(u，v，w).

引理2如果(p，q)图为非EMTL，则解空间δ(p，q，k)中一定不存在正整数k(k的取值范围为p+q+3≤k≤2(p+q))和q组(u，v，w)，使得相邻点u，v和边标号w的三元组(u，v，w)满足u+v+w=k，其中u，v，w∈[1，p+q]，并且u，v，w取值各不相同.

2 EMTL算法

根据EMTL定义，f(u)+f(v)+f(uv)=k，求和得公式

(1)

其中deg(vi)表示顶点vi的度，令vdc(vi)=deg(vi)-1，常数

得公式

(2)

由于公式(2)中只涉及到点的标号，无法遍历所有解空间，将所有边的标号系数设为0，并进行求和，得到公式

(3)

令

则有

q*k=C+S.

(4)

EMTL算法思想：

1)根据以上公式计算图G的度序列系数vdc(vi)、C、S的值，并将vdc(vi)、C、S的值代入到公式(4)，计算k的取值.

2)初始化f(vi)，按度序列由大到小的顺序进行标号.

(i)判断k的取值范围是否满足p+q+3≤k≤2(p+q)，若存在正整数k使得等式成立，则进入分配函数Labelling，否则，则对vdc(vi)与0组合做一次全排列.

(ii)若分配成功，则表示该图有EMTL，退出循环，算法结束；否则，则对vdc(vi)与0组合做一次全排列.循环执行此操作.

(iii)直到分配成功或者所有的全排列做完，则算法结束.

3)若全排列做完后该图还未标成功，则表示该图为非EMTL图.

EMTL算法描述：

输入：邻接矩阵

输出：标号矩阵

1 Calculatevdc(vi)、C;

2 is Conflict=true;

3 do

4 CalculateS;

5 if (C+S)%q==0

6 Calculatek;

7 if(Labelling(vdc(vi)，k))

8 is Conflict=false;

9 is Success=true;

10 return;

11 end if

12 end if

13 Find the rightvdc(vi)

14 while(is Conflict)

3 定理及证明

定理1对于双圈图G(p，q)，当4≤p≤15，均为EMTL图.

证明1) 对于双圈图G(p，q)，当4≤p≤15时，根据公式(4)可得边幻和常数12≤k≤62，对应的k-EMTL空间如表2所示.

表2 (p，p+1)图的k-EMTL空间 (p≤15)Tab.2 k-EMTL space for G(p，q) when p≤15

2) 利用EMTL算法，得到结果如表3所示.

表3 (p，p+1)图的EMTL (p≤15)Tab.3 EMTL for G(p，p+1) when p≤15

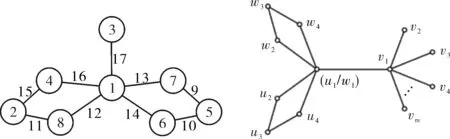
3)图2为G(15，16)成功标号示例.

定理2对于联图CnΔClSm，n=l，当3≤n≤5，m≥1时，具有EMTL.

证明设CnΔClSm的顶点集合分别为{u1，u2，…，un}、{w1，w2，…，wl}、{v1，v2，…，vm}.

1) 当n=3时，如图3所示.

|V(G)|=3+3+m-1=m+5，|E(G)|=3+3+(m-1)+1=m+6.

由公式(4)计算，边幻和常数K∈[2m+14，4m+22].当K=2m+14时，顶点标号为：

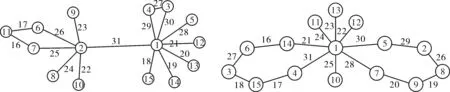
(a) G(15，16) (b) G(15，16)图2 图G(p，p+1)的EMTL示例图Fig.2 Examples for EMTL of G(p，p+1)

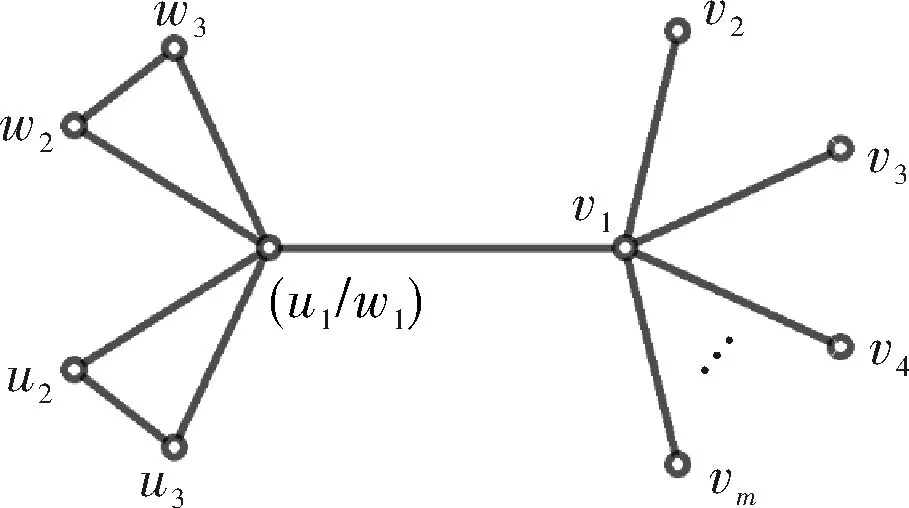
图3 C3ΔC3 SmFig.3 C3ΔC3 Sm

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={4，3，8，7}∪

{5，6，9}∪{10，11，…，m+8}，

f(V)={1，2，6}∪

{4，5}∪{3}∪{7，8，…，m+5}，

计算得边标号集合f(E)为

f(E)={2m+10，2m+11，2m+6，2m+7}∪

{2m+9，2m+8，2m+5}∪

{2m+4，2m+3，…，m+6}，

由于f(V)∪f(E)→[1，2m+11]，且f(V)∩f(E)=∅，故C3ΔC3Sm具有EMTL.

2) 当n=4时，如图4所示.

(a) C4ΔC4S1 (b) C4ΔC4Sm (m≥2)图4 C4ΔC4SmFig.4 C4ΔC4Sm

|V(G)|=4+4+m-1=m+7，

|E(G)|=4+4+(m-1)+1=m+8．

由公式(4)计算，边幻和常数K∈[2m+18，4m+30].当K=2m+19时，

i) 当m=1时，C4ΔC4S1的EMTL如图4(a)；

ii) 当m≥2时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={5，6，7，10，11}∪{4，8，9，13}∪

{12}∪{14，15，…，m+11}，

f(V)={1，2，5，9}∪{3，6，7}∪

{4}∪{8}∪{10，11，…，m+7}，

计算得边标号集合f(E)为

f(E)=

{2m+14，2m+13，2m+12，2m+8，2m+9}∪

{2m+15，2m+11，2m+10，2m+6}∪

{2m+7}∪{2m+5，2m+4，…，m+8}，

由于f(V)∪f(E)→[1，2m+15]，且f(V)∩f(E)=∅，故C4ΔC4Sm具有EMTL.

3) 当n=5时，如图5所示.

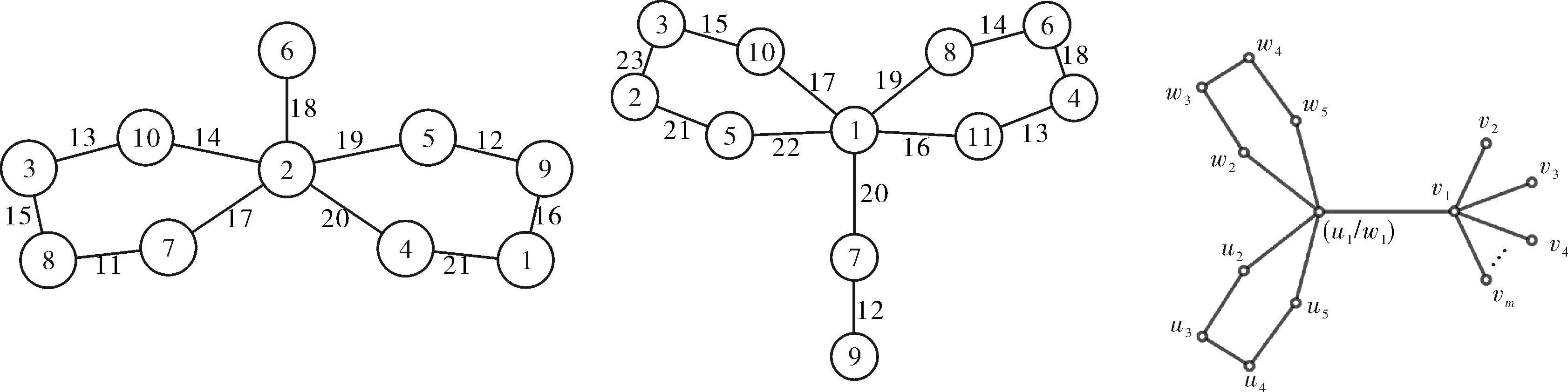
(a) C5ΔC5S1 (b)C5ΔC5S2 (c) C5ΔC5Sm(m≥3) 图5 C5ΔC5SmFig.5 C5ΔC5Sm

|V(G)|=5+5+m-1=m+9，

|E(G)|=5+5+(m-1)+1=m+10，

由公式(4)计算，边幻和常数K∈[2m+22，4m+38].当K=2m+24时，

i) 当m=1，2时，C5ΔC5S1、C5ΔC5S2的EMTL如图5(a)；

ii) 当m≥3时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={6，5，7，9，13，14}∪

{8，10，11，12，17}∪{15，16}∪

{18，19，…，m+14}，

f(V)={1，2，3，6，12}∪{4，7，8，9}∪

{5}∪{10，11}∪{13，14，…，m+9}，

计算得边标号集合f(E)为：

f(E)={2m+18，2m+19，2m+17，2m+15，

2m+11，2m+10}∪{2m+16，2m+14，

2m+13，2m+12，2m+7}∪{2m+9，2m+8}∪

{2m+6，2m+5，…，m+10}，

由于f(V)∪f(E)→[1，2m+19]，且f(V)∩f(E)=∅，故C5ΔC5Sm具有EMTL.

定理3对于联图CnΔClΔSm，当3≤n≤5，3≤l≤6，m≥2，具有EMTL.

证明设CnΔClΔSm的顶点集合分别为{u1，u2，…，un}、{w1，w2，…，wl}、{v1，v2，…，vm}.

1) 当n=3，l=3时，如图6所示.

图6 C3ΔC3ΔSmFig.6 C3ΔC3ΔSm

|V(G)|=3+3+m-2=m+4，|E(G)|=3+3+(m-1)=m+5，

由公式(4)计算，边幻和常数K∈[2m+12，4m+18].当K=2m+12时，顶点标号为：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={3，m+5，m+6}∪

{5，m+4，m+7}∪{4}∪{6，…，m+3}，

f(V)={1，2，m+4}∪{4，m+3}∪

{3}∪{5，6，…，m+2}，

计算得边标号集合f(E)为

f(E)={2m+9，m+7，m+6}∪

{2m+7，m+8，m+5}∪

{2m+8}∪{2m+6，2m+5，…，m+9}，

由于f(V)∪f(E)→[1，2m+9]，且f(V)∩f(E)=∅，故C3ΔC3ΔSm具有EMTL.

2) 当n=3，l=4时，如图7所示.

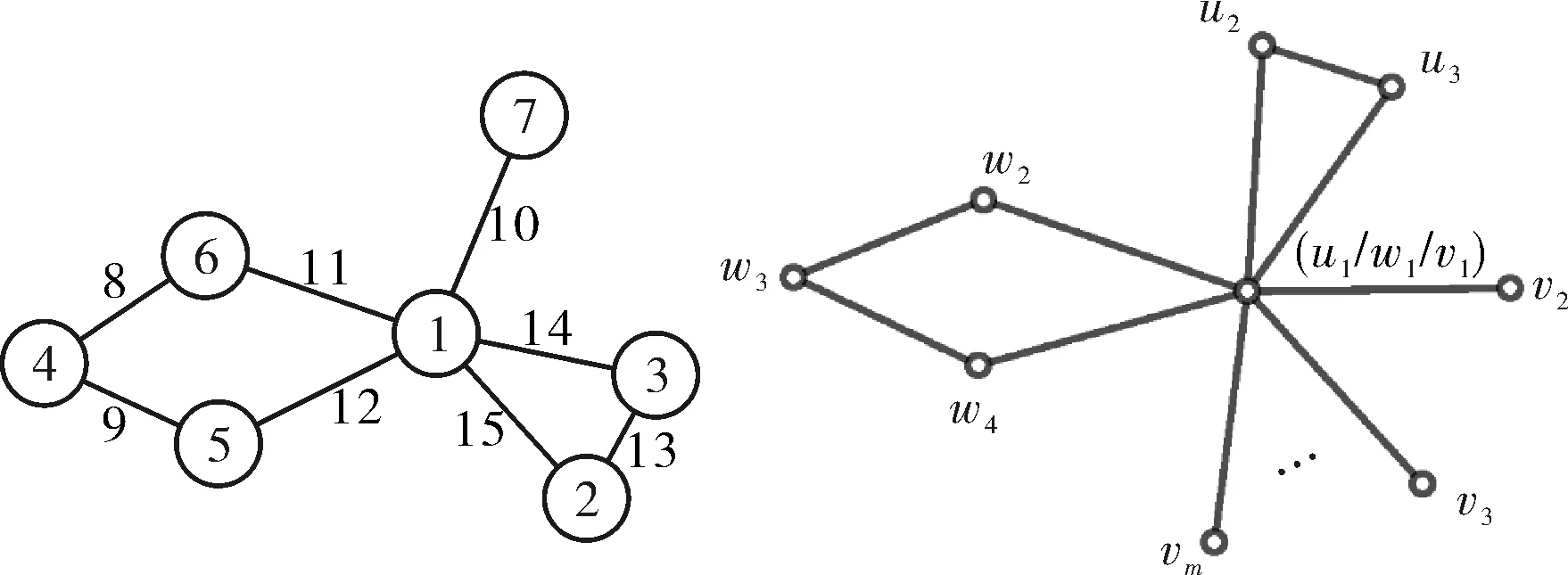
(a) C3ΔC4ΔS2 (b) C3ΔC4ΔSm (m≥3)图7 C3ΔC4ΔSmFig.7 C3ΔC4ΔSm

|V(G)|=3+4+m-2=m+5，|E(G)|=3+4+(m-1)=m+6，

由公式(4)计算，边幻和常数K∈[2m+14，4m+22].当K=2m+14时，

i) 当m=2时，C3ΔC4ΔS2的EMTL如图7(a)；

ii) 当m≥3时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={5，m+3，m+6}∪

{3，m+7，m+8，4}∪{6，7，…，m+2}∪

{m+4，m+5}，

f(V)={1，4，m+2}∪{2，m+5，3}∪

{5，6，m+1}∪{m+3，m+4}，

计算得边标号集合f(E)为

f(E)={2m+9，m+11，m+8}∪

{2m+11，m+7，m+6，2m+10}∪

{2m+8，2m+7，…，m+12}∪

{m+10，m+9}，

由于f(V)∪f(E)→[1，2m+11]，且f(V)∩f(E)=∅，故C3ΔC4ΔSm具有EMTL.

3) 当n=3，l=5时，如图8所示.

(a) C3ΔC5ΔS2 (b)C3ΔC5ΔS3 (c)C3ΔC5ΔS4 (d) C3ΔC5ΔSm (m≥5) 图8 C3ΔC5ΔSmFig.8 C3ΔC5ΔSm

|V(G)|=3+5+m-2=m+6，

|E(G)|=3+5+(m-1)=m+7，

由公式(4)计算，边幻和常数K∈[2m+16，4m+26].当K=2m+16时，

i) 当m=2，3，4时，C3ΔC5ΔS2、C3ΔC5ΔS3和C3ΔC5ΔS4的EMTL如图8(a)；

ii) 当m≥5时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={3，5，4}∪

{6，m+9，m+8，m+5，m+2}∪

{8，9，…，m+4}∪{m+6，m+7}，

f(V)={1，2，3}∪{5，m+4，4，m+1}∪

{7，8，…，m+3}∪{m+5，m+6}，

计算得边标号集合f(E)为

f(E)={2m+13，2m+11，2m+12}∪

{2m+10，m+7，m+8，m+11，m+14}∪

{2m+9，2m+8，…，m+12}∪

{m+10，m+9}，

由于f(V)∪f(E)→[1，2m+13]，且f(V)∩f(E)=∅，故C3ΔC5ΔSm具有EMTL.

4) 当n=3，l=6时，如图9所示.

(a) C3ΔC6ΔS2 (b) C3ΔC6ΔSm (m≥3)图9 C3ΔC6ΔSmFig.9 C3ΔC6ΔSm

|V(G)|=3+6+m-2=m+7，|E(G)|=3+6+(m-1)=m+8，

由公式(4)计算，边幻和常数K∈[2m+18，4m+30].当K=2m+19时，

i) 当m=2时，C3ΔC6ΔS2的EMTL如图9(a)；

ii) 当m≥3时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={5，m+4，m+7}∪

{4，m+10，m+9，m+8，m+11，6}∪

{7，8，…，m+3}∪{m+5，m+6}，

f(V)={1，4，m+3}∪

{3，m+7，2，m+6，5}∪

{6，7，…，m+2}∪{m+4，m+5}，

计算得边标号集合f(E)为

f(E)={2m+14，m+15，m+12}∪

{2m+15，m+9，m+10，m+11，m+8，2m+13}∪

{2m+12，2m+11，…，m+16}∪

{m+14，m+13}，

由于f(V)∪f(E)→[1，2m+15]，且f(V)∩f(E)=∅，故C3ΔC6ΔSm具有EMTL.

5) 当n=4，l=4时，如图10所示.

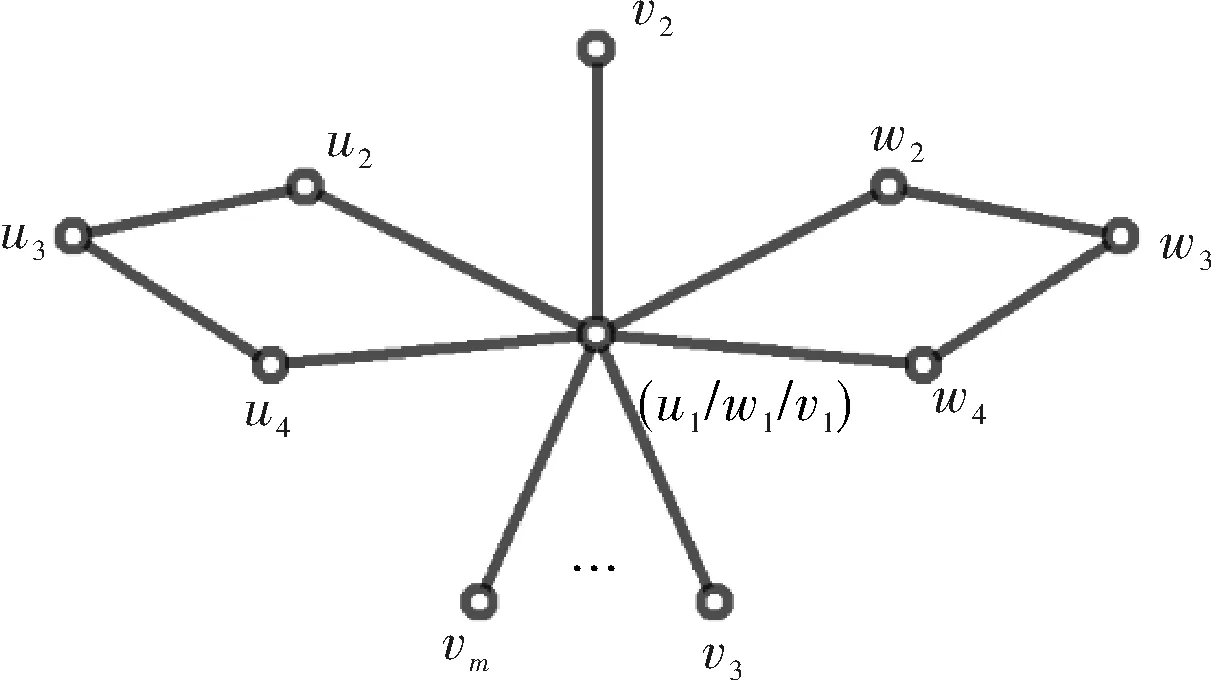
图10 C4ΔC4ΔSmFig.10 C4ΔC4ΔSm

|V(G)|=4+4+m-2=m+6，|E(G)|=4+4+(m-1)=m+7，

由公式(4)计算，边幻和常数K∈[2m+16，4m+26].当K=2m+17时，顶点标号为：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={5，6，m+8，m+7}∪

{m+5，m+9，m+10，m+6}∪

{4}∪{7，8，…，m+4}，

f(V)={1，4，2，m+6}∪

{m+4，5，m+5}∪{3}∪{6，7，…，m+3}，

计算得边标号集合f(E)为

f(E)={2m+12，2m+11，m+9，m+10}∪ {m+12，m+8，m+7，m+11}∪ {2m+13}∪{2m+10，2m+9，…，m+13}，

由于f(V)∪f(E)→[1，2m+13]，且f(V)∩f(E)=∅，故C4ΔC4ΔSm具有EMTL.

6) 当n=4，l=5时，如图11所示.

(a) C4ΔC5ΔS2 (b) C4ΔC5ΔSm (m≥3)图11 C4ΔC5ΔSmFig.11 C4ΔC5ΔSm

|V(G)|=4+5+m-2=m+7，|E(G)|=4+5+(m-1)=m+8，

由公式(4)计算，边幻和常数K∈[2m+18，4m+30].当K=2m+19时，

i) 当m=2时，C4ΔC5ΔS2的EMTL如图11(a)；

ii) 当m≥3时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={4，5，m+9，m+8}∪

{6，m+11，m+10，m+7，m+4}∪

{7，8，…，m+3}∪{m+5，m+6}，

f(V)={1，3，2，m+7}∪

{5，m+6，4，m+3}∪

{6，7，…，m+2}∪{m+4，m+5}，

计算得边标号集合f(E)为

f(E)={2m+15，2m+14，m+10，m+11}∪ {2m+13，m+8，m+9，m+12，m+15}∪ {2m+12，2m+11，…，m+16}∪ {m+14，m+13}，

由于f(V)∪f(E)→[1，2m+15]，且f(V)∩f(E)=∅，故C4ΔC5ΔSm具有EMTL.

7) 当n=5，l=5时，如图12所示.

(a) C5ΔC5ΔS2 (b) C5ΔC5ΔSm (m≥3)图12 C5ΔC5ΔSmFig.12 C5ΔC5ΔSm

|V(G)|=5+5+m-2=m+8，|E(G)|=5+5+(m-1)=m+9，

由公式(4)计算，边幻和常数K∈[2m+20，4m+34].当K=2m+22时，

i) 当m=2时，C5ΔC5ΔS2的EMTL如图12(a)；

ii) 当m≥3时，顶点标号如下：

图中相邻两点之和集合A、顶点标号集合f(V)分别为：

A={m+6，m+7，m+8，m+13，8}∪

{6，m+12，m+10，m+11，m+9}∪

{5，7}∪{9，10，…，m+5}，

f(V)={1，m+5，2m+6，7}∪

{5，m+7，3，m+8}∪{4，6}∪{8，9，…，m+4}，

计算得边标号集合f(E)为

f(E)={m+16，m+15，m+14，m+9，2m+14}∪

{2m+16，m+10，m+12，m+11，m+13}∪

{2m+17，2m+15}∪

{2m+13，2m+12，…，2m+17}，

由于f(V)∪f(E)→[1，2m+17]，且f(V)∩f(E)=∅，故C5ΔC5ΔSm具有EMTL.

猜测1对于双圈图CnΔClSm和CnΔClΔSm，当n≥6，l≥7，m≥1时，均有EMTL.

猜测2双圈图均为EMTL图.

4 结论

本文利用EMTL算法，得到了15个点内的所有双圈图的边幻和标号，从结果中分析找出两类联图CnΔClSm与CnΔClΔSm的标号规律，总结归纳了3条定理并给出证明，进而猜测：所有双圈图均有EMTL.