4WID 电动汽车转矩优化分配控制策略研究

陈哲明，程 灿，陈 宝，付江华

（重庆理工大学汽车零部件先进制造教育部重点实验室，重庆400054）

1 引言

4WID 电动汽车具有四个车轮的转矩独立可控的特性，且转矩分配比例可以灵活设置，这样就提供了一种可以改善汽车操稳性和平顺性的方法[1]，4WID 电动汽车运行稳定性研究有两种形式：电子差速控制和直接横摆力矩控制[2]。汽车运行轨迹受横摆角速度的影响较大，与电子差速相比，它的核心是利用车辆模型计算出车辆运行过程中的横摆角速度的实际值和理想值间的误差和误差变化率，并以此计算出维持车辆运行稳定所需的附加横摆力矩；利用算出的附加横摆力矩对各轮进行合理的转矩优化分配，使车辆更好的按照驾驶员的操纵意图运行。

现阶段4WID 电动汽车转矩优化分配控制一般采用分层控制，其中附加横摆力矩制定层可以采用滑膜变结构控制、LQR 控制等基于模型的控制算法，以及PID 控制、模糊控制等不基于模型的控制算法[3]；针对车轮力矩优化分配层的设计，有学者提出基于差动制动的横摆力矩控制策略[4]，也有提出基于等功率、等转矩的转矩分配方法[5]。由于这些方法研究目标的侧重点不同，使得控制效果也不同，且未能充分的到考虑轮胎利用率和电机峰值转矩对汽车的稳定性的影响。

故针对上述的不足，提出了基于轮胎利用率作为优化目标同时兼顾了电机的峰值转矩对汽车的运行影响的转矩分配控制策略，上层控制器选用模糊PID 控制，制定出稳定汽车运行所需的附加横摆力矩，再通过下层控制器将制定的横摆力矩通过优化函数算法分配给各车轮的轮毂电机从而维持汽车运行稳定。

整车控制策略结构图，如图1 所示。

图1 整车控制策略结构图FIg.1 Vehicle Control Strategy Structure

2 车辆动力学模型的建立

2.1 整车模型的建立

为研究和分析整车轮毂电机转矩优化控制策略，首先在Carsim 软件中建立整车模型。在Carsim 中选择B-Class 作为基准，选择车辆的初始状态，方向盘的转角δ、车速Vx为输入量，车轮的横摆角速度γ、质心侧偏角β、四个车轮的垂向力Fz、前轮转角σ1和σ2、四个车轮的纵向力Fx为输出量，并将输出的横摆角速度值作为实际值。B 级车参数，如表1 所示。

表1 B 级车参数Tab.1 Class-B Vehicle Parameters

2.2 二自由度参考模型的建立

二自由度车辆模型是理想模型能很好的反映出汽车运行的理想状态，因此选用此模型作为参考模型。在MATLAB/Simulink中建立二自由度理想模型。并对车辆做如下假设，忽略空气阻力和滚动阻力对车辆行驶状态的影响。将其输出的横摆角速度值作为理想值。

二自由度模型[6]可表示为：

转化为矩阵形式如下：

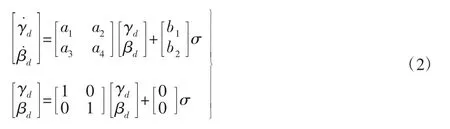
简化为状态空间方程为：

式中：vx—汽车纵向速度，m/s；σ—汽车前轮转角，（°）；m—汽车质量，kg；a，b—汽车质心至前后轴的距离，m；k1，k2—汽车前后轴的侧偏刚度，N/rad；Iz—为汽车绕z 轴的转动惯量，kg·m2。

2.3 轮毂电机模型

电机建模选用直流无刷永磁电机，该类型电机适合作为电动汽车动力装置，其特点为响应快、运行可靠。电机简化模型[7]，如图2 所示。

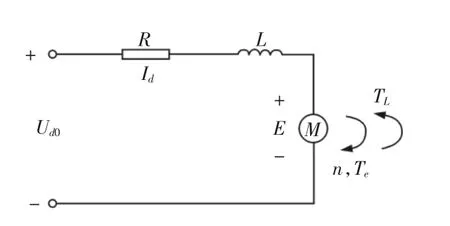
图2 电机简化模型Fig.2 Simplified Motor Model

电机动力学方程：

式中：Te—电动机产生的电磁转矩，单位为N·m；

ε—电机的阻尼系数；

TL—电机负载转矩，单位为N·m；

J—电机的转动惯量，单位为kg·m2。

2.4 轮胎模型

轮胎模型能反映出车轮在路面的附着情况同时其力学和参数特性影响着汽车行驶性能，在Carsim 中选用“魔术公式”轮胎模型[8]，其结构形式如下：y=Dsin｛Carctan［BX1-E（BX1-arctanBX1）］｝。

3 控制器设计

3.1 横摆力矩决策层

横摆力矩决策层是利用橫摆角速度实际值γ 与理想值γd来确定维持车辆稳定运行的附加横摆力矩。

先求解出横摆角速度的误差e（γ）和误差变化率e（γc），将其作为模糊控制的输入值。由于PID 控制策略中KP、KI、KD不能实时改变，且最佳参数不易获得，故利用模糊控制整定出PID 控制策略中最优KP、KI、KD，以此来利用PID 控制策略计算得出在不同运行条件下所需补偿给车辆的附加横摆力矩。

根据大量仿真试验经验，模糊控制算法输入和输出量的隶属度函数选用三角形隶属度函数，如图3～图6 所示。

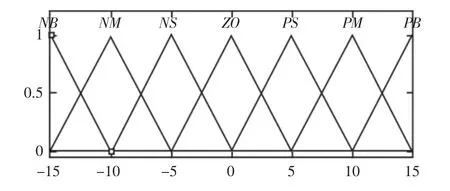
图3 e（γ）的隶属度函数Fig.3 The Membership Functions of e（γ）

图4 e（γc）的隶属度函数Fig.4 The Membership Functions of e（γc）

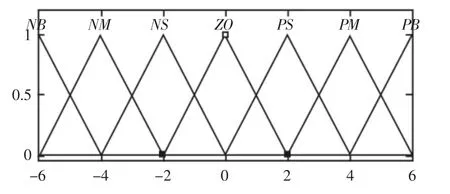
图5 KP 的隶属度函数Fig.5 The Membership Function of KP

图6 KI 和KD 的隶属度函数Fig.6 The Membership Function of KI and KD

表2 KP 的模糊规则Tab.2 The Fuzzy Rule of KP

模糊规则，如表2、表3 所示。

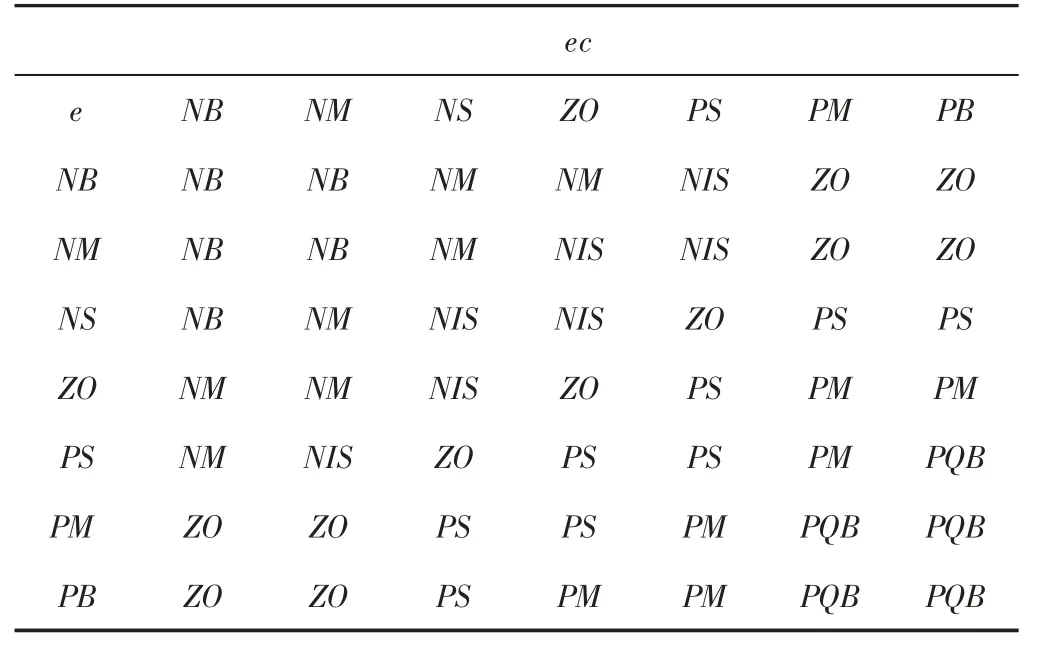
表3 KI 和KD 的模糊规则Tab.3 The Fuzzy Rule of KI and KD

3.2 驱动力矩分配层

关于驱动力矩的优化分配，利用优化分配算法来验证其对汽车操稳性的影响，且考虑到路面的附着条件和车轮的轮胎利用率等条件限制故选取轮胎利用率最小化作为优化的目标最为合理。

因此在转矩优化分配控制器中，将汽车的轮胎利用率作为各车轮转矩分配的优化目标函数，即以4 个车轮的侧向力Fymn和纵向力Fxmn的平方和除以垂直载荷Fzmn乘摩擦系数μ 的平方作为优化目标函数[9]，以此表示车辆的稳定裕度。当目标函数的数值趋近1 时，轮胎接近其附着极限，此时车辆将不能保持其行驶的稳定能力。所以优化目标是使轮胎利用率最小化，以保证车辆的稳定裕度最大化[10]，目标函数表示如下：

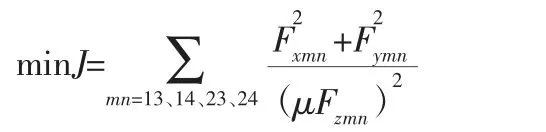
其中，m=1、2；n=3、41=f、2=r、3=l、4=r。

在实际中，由于受条件限制侧向力不能直接受到控制，故选择纵向力作为控制变量，此时优化函数可转换为：

因为电机所能输出的转矩大小受其峰值转矩的限制，所以选取Tmnmax为270N·m，故有不等式约束条件如下：

纵向力受到的不等式约束：

车辆所受等式约束还应满足下式：

由于fmincon 函数算法在MATLAB 中求解非线性多元函数最小值运用广泛且效果较好故采用fmincon 优化函数对转矩进行优化分配，在MATLAB 仿真软件中设计仿真程序语言将此问题转化成数学问题，定义输入变量：前轮转角σ1和σ2、附加横摆力矩MZ、路面的附着系数μ、总的纵向力Fx、四个车轮的垂向力Fzmn、各车轮的行驶纵向力Fxi。输出变量为四个车轮的力矩Fmn。

4 仿真验证

由于车辆在高附着路面和低车速行驶时，车辆能够较好的保持稳定行驶状态，施加此控制器对车辆稳定性的影响不大，故选取路面条件较差，附着系数较低的路面，此时μ=0.4，同时验证车辆在中高速的稳定性，故选取车速分别为60km/h 和100km/h。车辆的方向盘输入，如图7 所示。

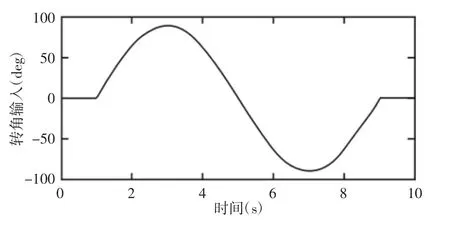
图7 车辆的方向盘转角输入Fig.7 Vehicle Steering Wheel Angle Input

当路面的附着系数μ=0.4，车速为60km/h，此时为中速条件，车辆的附加横摆力矩和优化转矩分配，如图8、图9 所示。

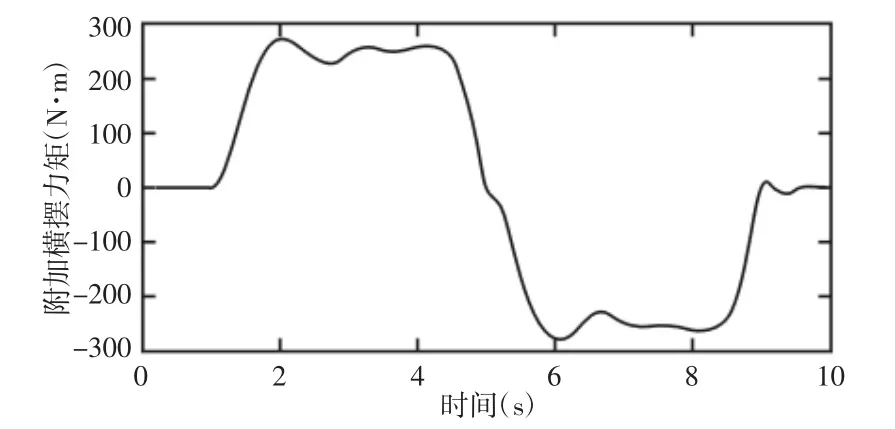
图8 车辆的附加横摆力矩Fig.8 Additional Yaw Moment for Vehicles

图9 优化转矩分配Fig.9 Optimize Torque Distribution

车辆在无控制、优化控制和平均分配控制的状态下的横摆角速度、质心侧偏角和“横摆角速度-质心侧偏角”相图，如图10～图12 所示。

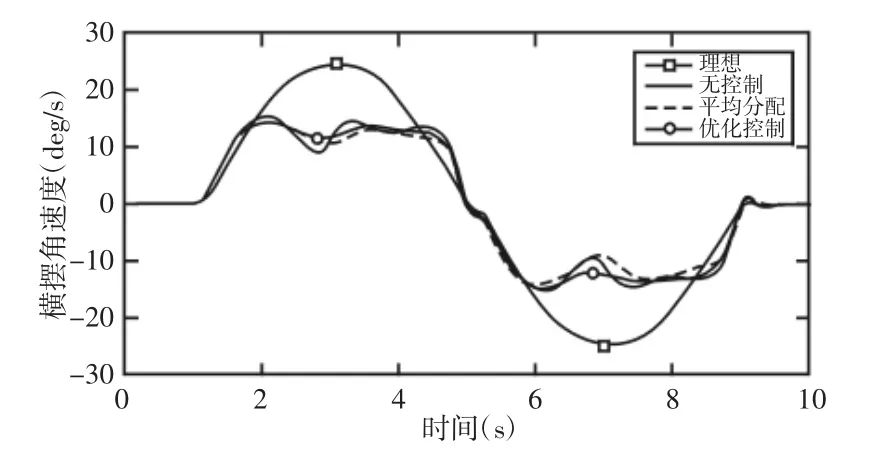
图10 横摆角速度对比图Fig.10 Yaw Angle Speed Comparison Chart

图11 质心侧偏角对比图Fig.11 Centroid Side Angle Comparison Chart

图12 “质心侧偏角—横摆角速度”相图Fig.12 "Center of Mass Yaw Angle-Yaw Rate" Phase Diagram

如上图所示，施加控制器对车辆的四个车轮进行力矩优化分配，对比图10 和图11 可以看出优化分配比平均分配控制要更好的跟踪理想值，“横摆角速度-质心侧偏角”相图中优化分配比平均分配要更收敛，汽车运行要更加的平稳。

当汽车高速行驶时，设定车辆运行速度为100km/h，路面的附着系数μ=0.4，车辆容易出现失稳，对于汽车的操稳性要求更加严格。此时车辆的附加横摆力矩和转矩优化分配，如图13、图14所示。

图13 车辆的附加横摆力矩Fig.13 Additional Yaw Moment for Vehicles

图14 优化转矩分配Fig.14 Optimize Torque Distribution

如图15～图17 所示。在车辆的运行的速度为100km/h，路面的附着系数μ=0.4 时“横摆角速度-质心侧偏角”相图中优化分配控制比平均分配的质心侧偏角要更加收敛，汽车运行的稳定性要更好，如图17 所示。考虑到电机和路面的附着对汽车的约束，本控制策略对汽车在不同的车速下的操稳性具有良好的效果。

图15 横摆角速度对比图Fig.15 Yaw Angle Speed Comparison Chart

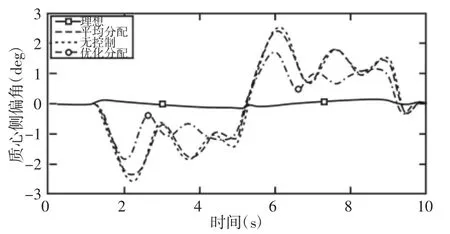
图16 质心侧偏角对比图Fig.16 Centroid Side Angle Comparison Chart

图17 “质心侧偏角—横摆角速度”相图Fig.17 "Center of Mass Yaw Angle-Yaw Rate" Phase Diagram

5 结论

由于4WID 电动汽车具有各车轮转矩分配实时优化的优势，在充分利用横摆角速度这个重要的车辆稳定表征物理量，设计了一种转矩优化分层控制策略。利用模糊控制和PID 控制的理论指导，建立附加横摆力矩决策控制器，制定出维持车辆稳定的附加横摆力矩，进而运用优化分配函数对转矩进行优化分配，其中转矩优化分配方法改善了平均转矩分配的不足之处，同时考虑了电机峰值转矩和路面附着对汽车运行工况的影响，使得车轮转矩更趋近真实值选取并通过低附着路面和不同的车速条件下对本控制策略进行了仿真。仿真结果证明此种控制策略能够很好的控制汽车质心侧偏角，提高了车辆的行驶稳定性。