六臂井径测井仪推靠系统运动学分析及仿真

任 涛，张 飞，孙 文

（西安石油大学机械工程学院，陕西 西安 710065）

1 引言

井径测井仪是石油测井领域内一种十分重要的石油测井设备，而推靠系统是井径测井仪完成井筒直径大小测量的主要组成部分[1]。目前，关于井径测井仪推靠系统传动机构的运动学分析研究较少，缺乏详细的数学分析模型，因而无法准确描述推靠系统的运动规律和真实的运动状态，而推靠系统运动性能的好坏与测井数据的准确性密切相关。因此，为了更好地了解井径测井仪推靠系统的工作状态，应用复数矢量法建立推靠系统精确的数学模型，对其进行运动参数分析，描述其运动规律。虚拟样机技术通过CAD/CAM/CAE 等技术手段把产品资料集成到一个可视化环境中，实现产品的仿真、分析。运用Adams/View 模块建立推靠系统模型，并虚拟仿真其运动，进一步辅助分析了其运动规律，为后续推靠系统动力学分析及结构参数优化提供了理论依据[2]。

2 基于Pro/E 建立六臂井径测井仪

通过Pro/E 对六臂井径测井仪进行建模[3]，如图1 所示。仪器内部结构示意图，如图2 所示。其推靠系统机械传动主要包括：电机、电机连接轴、丝杠、推杆防转套、大推杆、耐磨杆、耐磨杆推杆、销钉、支撑臂、小推杆、活动杆、活塞杆、弹簧、弹簧盒接头、压盖。工作原理：打开过程中，电机带动丝杠转动，推杆防转套将丝杠转动转化为大推杆、小推杆向右匀速移动，小推杆带动支撑臂向右移动并转动，推靠臂（由耐磨杆、耐磨杆推杆、活动杆组成）在活塞杆弹簧预紧力和支撑臂的作用下打开，推靠臂运动到井壁，通过行程限位开关控制传动系统自锁装置实施自锁，电机停转。测量过程中，整个仪器在匀速提升过程中，随着井径的变化，推靠臂转动且发生张缩，将径向位移转化为活塞杆的轴向位移。给传感器一定强度电流，把井径变化转化为电位差的变化，连续测量电位差即可获得井径曲线，来反映井径变化的大小。

图1 六臂井径测井仪三维图Fig.1 Three-Dimensional Diagram of the Six-Arm Caliper Tool

图2 六臂井径测井仪内部结构示意图Fig.2 Schematic Diagram of the Internal Structure of the Six-Arm Caliper Tool

3 推靠系统运动状态分析

为了保证六臂井径测井仪具有确定的运动，需要计算推靠系统的自由度。此机构自由构件数n 为4（即推杆1，支撑臂2，推靠臂3，活塞杆4），低副p1个数为4（2 个转动副A、B 和2 个移动副C、D），高副ph个数为2（凸轮副E 和槽销副F），如图3 所示。机构自由度F 为：

由机械原理可知，如果机构的原动件数目小于机构的自由度，机构运动将不完全确定[4]。

六臂井径测井仪有两种运动状态，即推靠系统打开运动状态和测量运动状态[5-6]。打开过程中，支撑臂与推靠臂铰接处由于弹簧预紧力的作用，销钉只在槽销副一端转动而没有相对移动，槽销副的作用等同于转动副。于是机构低副个数为5（3 个转动副A、B、F 和2 个移动副C、D），高副个数为1（凸轮副E）。因此，机构打开运动状态自由度为1。测量过程中，由于电机的停转，推杆1停止移动。自由构件数为3（即支撑臂2，推靠臂3，活塞杆4），低副个数为3（2 个转动副A、B 和1 个移动副C），高副个数为2（凸轮副E 和槽销副F）。该机构测量运动状态自由度为1。所以，六臂井径测井仪推靠系统两种状态都有确定的运动。

图3 推靠系统运动简图Fig.3 Motion Diagram of the Pushing System

4 用复数矢量法做推靠系统运动学分析

复数矢量法是平面连杆机构运动分析的一种解析法。将各杆件用矢量表示，根据机构的结构建立封闭矢量位置方程，将位置方程对时间求一次和二次导数获得机构的速度和加速度方程，求出所需的速度和加速度，进而得到机构的运动性能[7-8]。

4.1 推靠系统打开状态数学模型

已知AG=e、AH=e1、HE=k，推杆起始位置为E，以速度v 向右运动，如图4 所示。设AE、ED、AD、DB、AB、AC 对应的长度分别为S1、S2、l1-0、l2、S3-0、l4，所对应方位角（杆件与x 轴正方向夹角，沿逆时针方向为正）分别为θ0、0、θ1-0、θ2-0、θ3-0、θ4-0，且θ3-0＝θ4-0，对应的矢量分别为

图4 推靠系统打开状态矢量图Fig.4 Vector Illustration of the Open State of the Push System

4.1.1 推靠系统打开状态矢量位置方程分析

将上式改写成复数形式：

按欧拉公式展开：

（2）以矢量三角形ADB 分析支撑臂的转角θ2-0，推靠臂的转角θ3-0的和C 点的位置。

将上式改写成复数形式：

按欧拉公式展开：

解得：

其中，A=2l1-0l3-0cosθ1-0；B=2l1-0l3-0sinθ1-0D=2l1-0l2cosθ1-0；E=2l1-0l2sinθ1-0；

推靠臂C 点的位置为：

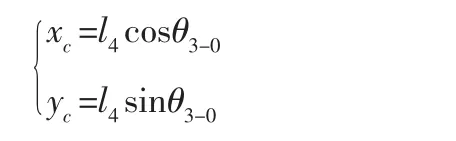
4.1.2 推靠系统打开状态速度方程分析

将式（3）对时间t 求导数得：

式中：˙l1-0—构造杆的相对速度；ω1-0—构造杆的牵连角速度。

（2）以矢量三角形ADB 分析支撑臂的角速度ω2-0、推靠臂的角速度ω3-0和C 点速度vC-0。

将式（6）对时间求导数得：

为消去ω3-0，（10）式两边乘以得：

为消去ω2-0，（10）式两边乘以得：

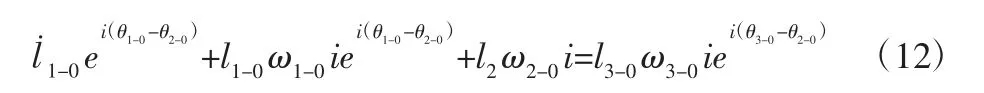
式（11）、式（12）按欧拉公式展开，取实部得：

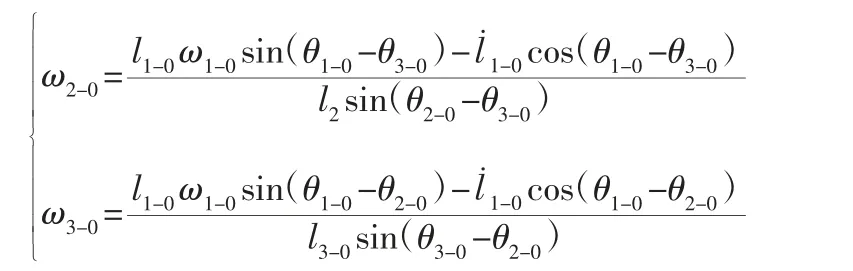
推靠臂C 点速度vC-0为：vC-0=l4ω3-0

4.1.3 推靠系统打开状态加速度方程分析

将式（8）对时间t 求导数得：

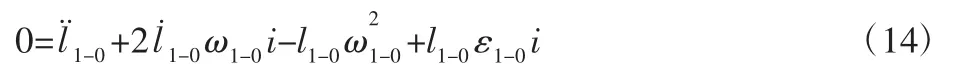
式（14）公式展开得：

（2）以矢量三角形ADB 分析支撑臂的角加速度ε2-0、推靠臂的角速度ε3-0和C 点加速度aC-0。

将式（10）对时间t 求导数得：

为消去ε3-0，式（15）两边乘以得：

为消去ε2-0，式（15）两边乘以得：

式（16）、式（17）按欧拉公式展开，取实部得：

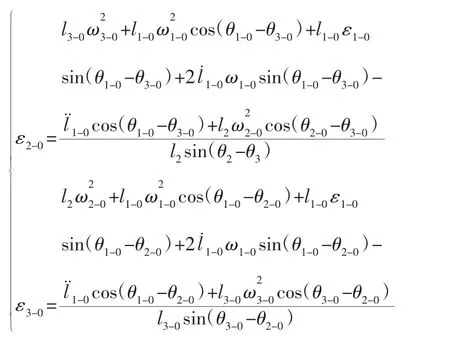
推靠臂C 点加速度aC-0为：

4.2 推靠系统测量状态数学模型

已知AG=e、AH=e1、HD=k1，推靠臂以匀角速度ω3-1向绕A右点转动，如图5 所示。设AD、DB、AB、AC 对应的长度分别为l1-1、l2、l3-1、l4，所对应方位角（杆件与x 轴正方向夹角，沿逆时针方向为正）分别为θ1-1、θ2-1、θ3-1、θ4-1，且θ3-1＝θ4-1，对应的矢量分别为

图5 推靠系统测量状态矢量图Fig.5 Vector Illustration of the Measurement State of the Push System

4.2.1 推靠系统测量状态矢量位置方程分析

以矢量三角形ADB 分析铰接位置槽销高副B 处的位置、推靠臂C 端的位置及支撑臂的转角θ2-1。

将上式改写成复数形式：

按欧拉公式展开：

为消去l3-1，式（20）两边乘以得：

由式（21）、式（22）解得：

4.2.2 推靠系统测量状态速度方程分析

以矢量三角形ADB 分析铰接位置槽销副B 处的速度vB、推靠臂C 端的速度vC-1及支撑臂的角速度ω2-1。

将式（20）对时间t 求导数得：

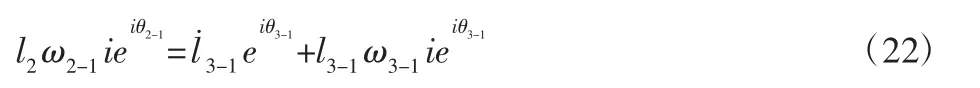
式中：l˙3-1—l3-1的相对速度；牵连角速度。为消去ω2-1，式（23）两边乘以得：

为消去l˙3-1，式（23）两边乘以得：

式（23）、式（24）按欧拉公式展开，分别取实部和虚部得：

铰接位置槽销高副B 的速度为：vB=l2ω2-1

推靠臂C 端的速度为：vC-1=l4ω3-1

4.2.3 推靠系统测量状态加速度方程分析

以矢量三角形ADB 分析铰接位置槽销副B 处的加速度aB、推靠臂C 端的加速度aC-1及支撑臂的角加速度ε2-1。

将式（22）对时间t 求导数得：

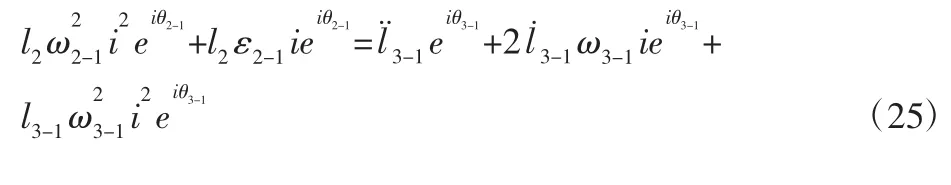
为消去ε2-1，式（25）两边乘以得：

式（26）、式（27）按欧拉公式展开，分别取实部和虚部得：

铰接位置槽销副B 点的加速度为：

推靠臂C 端的加速度为：aC-1=0

5 推靠系统推靠臂结构参数化设计及凸轮运动特性分析

5.1 偏心圆弧线型推靠臂结构参数化设计

偏心圆弧线型推靠臂结构示意图，如图6 所示。图中：e—偏心圆圆心O′与坐标原点O 的距离（即上述AG）；r—偏心圆半径；φ—偏心圆上M 点与轴线的夹角。通过计算得偏心圆弧线的直角坐标方程为：

图6 偏心圆弧线型推靠臂结构示意图Fig.6 Schematic Diagram of the Eccentric Circular Arc Type Push Arm Structure

5.2 偏心圆弧线型推靠臂凸轮运动特性分析

推靠系统中，推靠臂和活塞杆组成的是直动从动件偏心圆弧线凸轮机构，如图7 所示。

通过图中几何关系计算可得活塞杆的运动方程为：

（1）推靠系统打开过程中，推靠臂以角速度ω3-0转动，转过的角度为θ3-0，即θ3-0＝ω3-0t，则活塞杆的运动方程为：

式中：ω3-0—变角速度。

（2）推靠系统测量过程中，推靠臂以角速度ω3-1转动，转过的角度为θ3-0，即θ3-1=ω3-1t，则活塞杆的运动方程为：

式中：ω3-1—匀角速度。

将式（31）对时间t 求一次导和二次导，活塞杆的速度方程和加速度方程分别为：

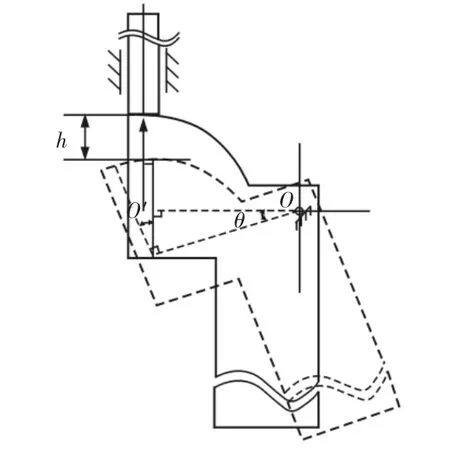
图7 直动从动件偏心圆弧线凸轮机构Fig.7 Direct-Acting Follower Eccentric Circular Arc Cam Mechanism

分析可知，推靠系统中，偏心圆弧线型凸轮机构活塞杆在两种运动状态下均不是匀速运动。

6 推靠系统运动学仿真

6.1 建立推靠系统打开状态几何模型及运动学仿真

设计的六臂井径测井仪是测量8.5 寸（即）裸眼井，工作过程中推靠系统六个臂的运动状态是相同的，所以通过简化模型，运用Adams 中的Adams/View 界面对单个推靠系统进行结构参数化设计[9]。

6.1.1 推靠系统打开状态几何模型

已知位置参数AG=21mm、AH=23.5mm、HE=40mm，推杆以速度v=3mm/s 向右运动。推靠系统打开状态几何模型，如图8 所示。

图8 推靠系统打开状态几何模型Fig.8 The Geometric Model of the Open State of the Pushing System

（1）构件的创建

每个构件基本参数如下，推靠臂长473mm、宽17mm、高11mm；偏心圆半径r 为13mm；滑柱1 是小半径3.5mm、大半径30mm、高10mm 的空心圆柱；滑柱2 是小半径5.5mm、大半径40mm、高10mm 的空心圆柱；支撑臂是长137.5mm，宽10mm，高5.3mm 连杆；推杆长150mm、宽15mm、高17mm；活塞杆长200mm，由半径5mm、长66mm 的圆柱体和半径3.25mm、长134mm 的圆柱体组成。

（2）运动副的创建

建立推杆和地面的移动副、活塞杆和地面之间的移动副、活塞杆和推靠臂的凸轮副、推靠臂和地面之间的转动副、推靠臂和支撑臂之间的转动副、支撑臂和推杆之间的转动副、滑柱和地面之间的固定副。

（3）运动驱动的创建

建立推杆和地面的平移驱动并修改运动函数为2.0*time。

（4）传感器的创建

运用Adams/Dsign Exploration 创建一个感知推靠臂运动到井壁位置的传感器，保证推靠臂C 端运动到井壁停止。

6.1.2 仿真与测试

设置仿真终止时间为5s，仿真步数为100。

（1）测量推靠臂C 点位置x 轴方向位移，如图9 所示。

图9 推靠系统中推靠臂x 轴方向位移曲线Fig.9 The Displacement Curve of the Push Arm in the x-axis Direction of the Pushing System

由图9 可知，推杆以2mm/s 的速度运动时，推靠臂C 端运动到8.5 寸井壁停止所需时间约为4.2s。

（2）测量推靠臂转角、角速度、角加速度，如图10 所示。

图10 推靠臂转角、角速度、角加速度曲线Fig.10 Push Arm Angle，Angular Velocity，Angular Acceleration Curve

由图10 可知，分动式推靠系统打开过程中，推靠臂不是以恒定角速度转动的，与理论推导一致。

（3）测量推靠臂C 端速度、加速度，如图11 所示。

图11 推靠臂C 端速度、加速度曲线Fig.11 Push arm C speed and Acceleration Curve

由图11 可知，分动式推靠系统打开过程中，推靠臂不是以恒定速度转动的。

（4）测量推靠系统中活塞杆质心位移、速度、加速度，如图12所示。

由图12 可知，活塞杆的运动是变速运动，与理论推导一致。因初始速度有突变，活塞杆出现突变加速度，从而使推靠臂受到极大的冲击，引起测井仪的振动。

图12 推靠系统中活塞杆质心位移、速度、加速度曲线Fig.12 The Displacement，Velocity and Acceleration Curves of the Piston Rod in the Push System

6.2 建立推靠系统测量状态几何模型及运动学仿真

因为测量裸眼井的工况比较复杂，所以进行推靠系统测量状态运动学仿真是很难实现的。模拟推靠系统测量规则井径，进一步验证其运动规律。

6.2.1 推靠系统测量状态几何模型

已知AG=21mm、AH=23.5mm、HD=74mm，推靠臂以角速度ω3-1=4rad/s 绕A 点转动。推靠系统测量状态几何模型，如图13 所示。推靠系统测量状态建模步骤基本和上述一致，不同点：支撑臂和推靠臂的转动副改为槽销副，推杆的移动副改为固定副，推靠臂驱动函数为：IF（SIN（PI*TIME）：-4d，0，4d）[10]。

图13 推靠系统测量状态几何模型Fig.13 Geometric Model of the Measurement State of the Push System

6.2.2 仿真与测试

设置仿真终止时间为4s，仿真步数为100。

（1）测量推靠臂C 点位置x 轴方向位移、速度、加速度，如图14 所示。

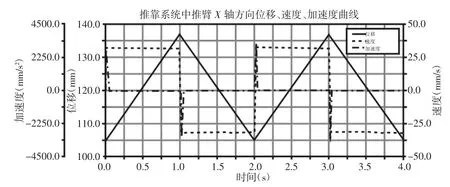
图14 推靠系统中推靠臂x 轴方向位移、速度、加速度曲线Fig.14 The Displacement，Velocity and Acceleration Curves of the Push Arm in the X-Axis Direction of the Pushing System

由图14 可知，在井径变化范围小的情况下，推靠臂径向位移可以看作是时间的一次函数，与理论计算一致。井径变化和推靠臂径向位移变化相同，因此客观的模拟出推靠系统测量规则井径的运动状态。

（2）测量推靠系统活塞杆质心位移、速度、加速度，如图15所示。

图15 推靠系统活塞杆质心位移、速度、加速度曲线Fig.15 The Displacement，Velocity and Acceleration Curves of the Piston Rod in the Push System

由图15 可知，由于探测臂只在（±4）°内转动，活塞杆的速度仅有微小变化，所以活塞杆不是匀速运动。因换向速度有突变，出现突变加速度，会使推靠臂受到极大冲击，从而引进测井仪的振动。

7 结语

（1）通过分析研究，六臂井径测井仪推靠系统在打开、测量两种运动状态都有确定的运动。（2）利用复数矢量法对推靠系统进行了运动学分析，推导了推靠系统的矢量位置方程、速度方程和加速度方程，得出了两种运动状态下输出运动与输入运动的位置、速度及加速度之间的关系，为进行推靠系统动力学分析奠定了基础。（3）通过Adams 虚拟仿真分析验证了理论模型的合理性。并发现在启动、换向时因速度有突变，活塞杆会出现突变加速度，使推靠臂受到极大的冲击，从而引进机器的振动。怎样减弱这种冲击带来的不利影响，是后续二次优化所要研究的重点。