异形斜拉桥塔梁结合段应力状态与剪力滞效应研究

罗 宜 张华华

(1.湖北省交通规划设计院股份有限公司 武汉 430051； 2.宜昌市夷陵区城市建设项目办公室 宜昌 443100)

斜拉桥跨越能力强、造型美观，在大跨径桥梁中具有较大优势，且经常被作为地标性建筑。斜拉桥的内部连接方式有：漂浮体系、半漂浮体系、塔梁固结体系、塔墩铰接体系、刚构体系等[1]。塔梁结合段采用刚构体系时，斜拉桥体系适合悬臂施工，但温度和混凝土的收缩徐变引起的次内力较大，常常以此控制设计；塔梁固结体系具有较大刚度，多用在独塔体系中，但塔梁固结处主梁会产生巨大的负弯矩[2-3]。塔梁结合段一般具有以下特点：①构造通常较为复杂；②主梁、索塔和斜拉索之间的受力会互相影响；③混凝土箱梁的主梁通常会配置三向的预应力；④存在剪力滞效应。因此，塔梁结合段的应力状态十分复杂，给配筋设计带来了困难。

1 项目背景及有限元模型

某空间双索面独塔斜拉桥，桥跨组成为150 m+150 m。主桥采用塔墩梁固结体系，桥面宽42 m。汽车荷载为城-A 级，人群荷载按CJJ 11-2011 《城市桥梁设计规范》规定执行。

主梁采用C55混凝土，主塔塔柱和横梁采用C50混凝土，其中，横梁合龙段和塔顶合龙段均采用微膨胀混凝土；塔座、承台采用C40 混凝土，桩基采用水下C30混凝土。斜拉索采用PES(C)新型拉索体系，钢丝采用直径7 mm的镀锌高强度低松弛平行钢丝，其抗拉强度标准值为1 670 MPa。

主梁采用单箱三室预应力混凝土等高连续箱梁，梁高3.3 m，标准节段长24 m，张拉纵向和横向预应力。索塔为单塔，总高度为90 m，索塔轴线为平面椭圆曲线，且轴线所在平面与水平面垂直。桥塔截面采用空心矩形截面。单侧的斜拉索44根，全桥共88根。

2 有限元模型

2.1 全桥模型

采用有限元分析软件midas Civil建立全桥杆系分析模型，主梁和主塔采用梁单元，斜拉索采用杆单元。整个模型有354个结点，255个梁单元，88个桁架单元。有限元模型见图1。

图1 全桥有限元模型图

2.2 塔梁结合段局部有限元模型

在局部分析中，一般运用圣维南原理，截取拟分析局部部位两侧一定宽度的隔离体作为局部分析对象，以此来分析桥梁局部应力状态和变形[4-6]。

采用midas FEA有限元仿真分析软件进行计算。按照设计图纸建立塔梁固结处的精细实体模型，实体中的所有挖空和倒角都考虑在内。预应力主要考虑主梁纵向预应力和横向预应力，预应力钢束用软件中的钢筋单元进行模拟。

主梁部分截取0号节段，共22 m长，主塔部分取塔底至主梁中心线处标高以上8 m的位置。建模时先建立几何模型，再划分网格。整个模型一共303 166个单元，共114根预应力钢筋。有限元模型见图2、图3。

图2 有限元模型轴视图

2.3 荷载和边界条件

局部计算模型的边界条件采用塔底固结，梁端及塔上部截取截面处施加整体计算得出的轴力、弯矩和剪力。其他荷载还包括结构自重、预应力。整体有限元分析得到的各截取面的内力值见表1。

表1 截面内力

3 塔梁结合段应力分析

为了凸显塔梁结合段处的局部应力特点，本文给出的应力云图结果中隐去了离结合段处较远的部分单元，在2.3小节中的荷载及边界条件下，得到了局部模型的应力云图结果见图4、图5。

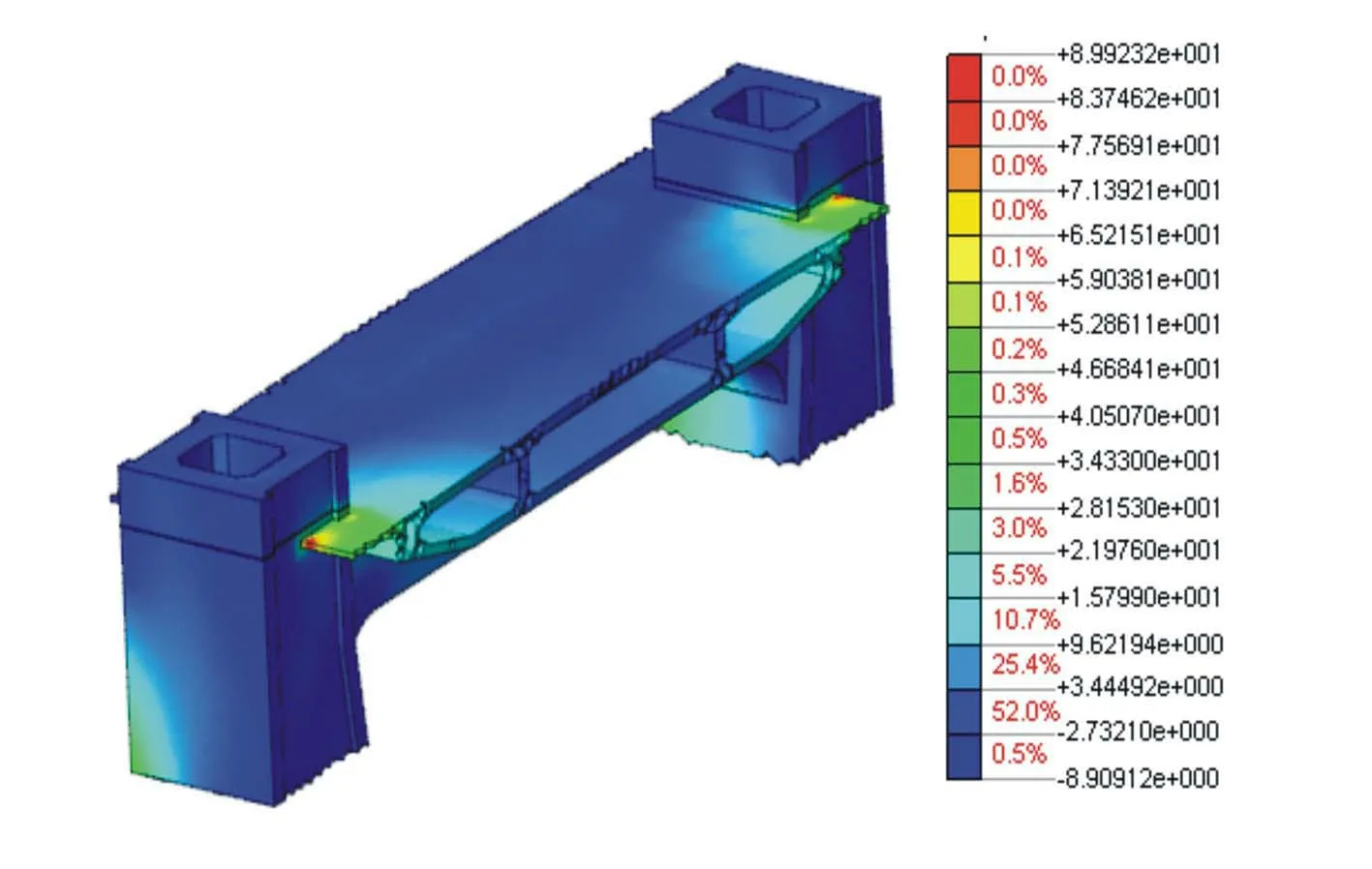
图4 塔梁连接局部第一主应力(单位：MPa)

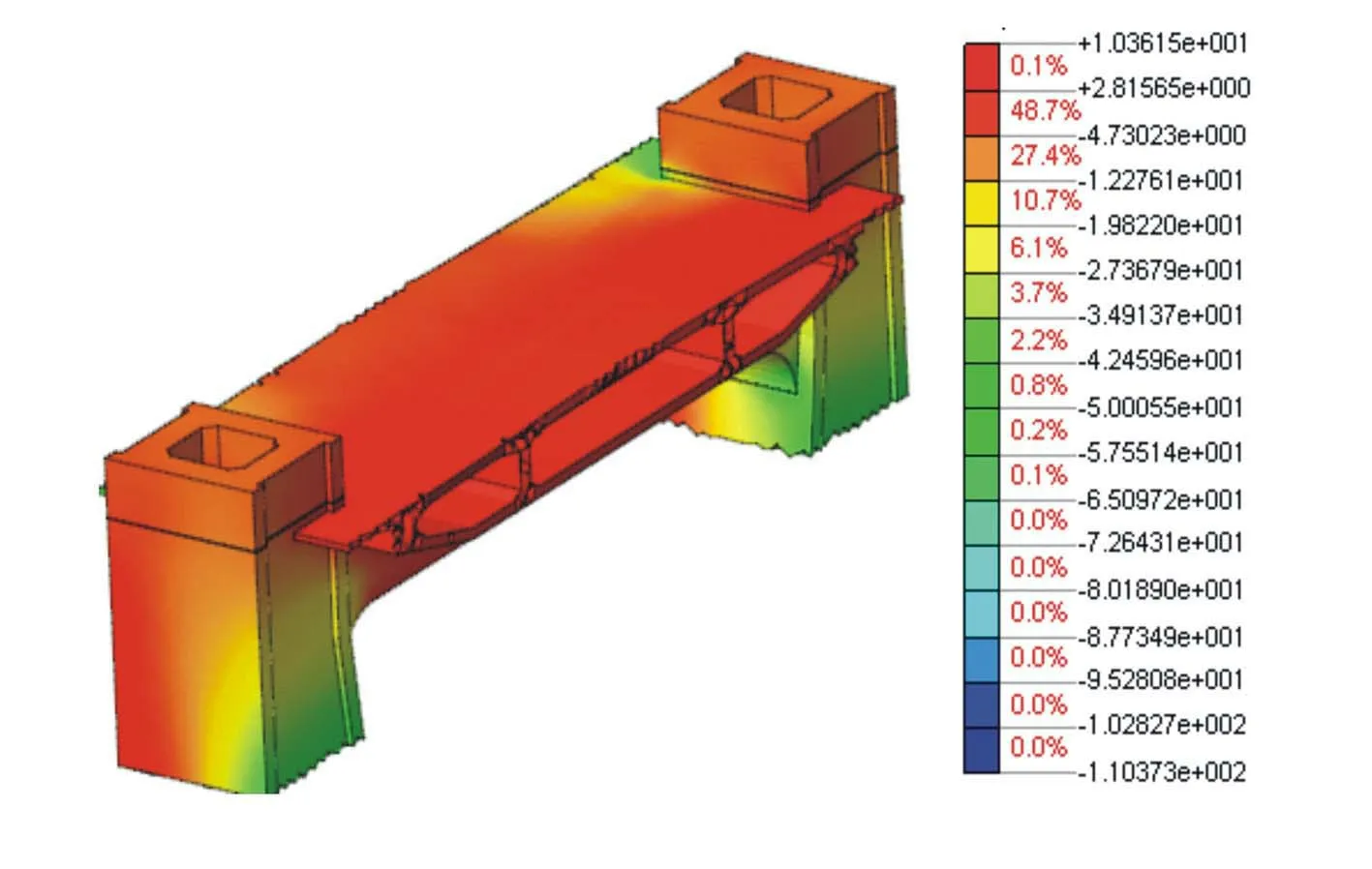
图5 塔梁连接局部第三主应力(单位：MPa)

由图4可见，塔梁固结段处的拉应力在塔梁交界突变处最大，远离此处时拉应力逐渐变小，直至变为压应力。局部模型中，拉应力分布占比约为47.5%，压应力占比约为52.5%；拉应力的数值分布在3～15 MPa之间，而数值在3 MPa附近的占比较大，达到30%，分布在塔梁交界较远的位置；数值在9.5 MPa附近的占比约为10%，集中分布在主梁悬臂端部与主塔交界处。由于结构尺寸的突变，导致塔梁连接处存在应力集中，拉应力中出现较大值，但是这部分值所占比例极小，可以忽略，不影响结构的整体安全。

由图5可见，压应力主要集中在-27～-4.7 MPa之间。其中，数值在-19 MPa左右的压应力约占12%，数值在-12 MPa左右的压应力约占28%，数值在-4.7 MPa左右的压应力约占50%。另外，之所以产生较大压应力，是由于预应力具有巨大应力，钢束端部引起应力集中，这是实体有限元模型中难以避免的现象，因此可以忽略此影响。

综合以上论述，图4、图5所示局部模型整体处于较为均匀的受压状态，拉应力主要集中在塔梁交界突变处及附近位置，对整体受力影响不大。因此，进行此结合段局部设计时，应注意减小结构尺寸突变，增加倒角等过渡；同时，应根据拉应力和压应力的分布特点，适当增加钢筋配置以防止局部应力裂缝的产生。

4 塔梁结合段剪力滞效应分析

对于箱梁结构，在对称弯曲荷载作用下，如果箱梁具有初等弯曲理论中所假定的无限抗剪刚度(即变形的平截面假定)，那么弯曲正应力沿梁宽方向是均匀分布的。但是，箱梁产生的弯曲的横向力(压应力)通过肋板传递给翼板，而剪应力在翼板上的分布是不均匀的，在交接处最大，远离肋板时逐渐减小。沿翼板分布的不均匀的剪切变形引起弯曲时，远离肋板的翼板的纵向位移滞后于肋板附近的纵向位移，所以其弯曲正应力的横向分布呈曲线形状，这种现象称之为“剪力滞效应”[7-8]。

4.1 模型说明

本节分析塔梁结合段的剪力滞效应及其分布规律。为了得到更精细的剪力滞分布结果，在第3小节的局部分析模型的基础上，本节中的计算模型考虑所截取部分结构内包含的4个横隔板。模型截面取标准截面。有限元模型见图6。

图6 剪力滞分析有限元模型

4.2 计算荷载和边界条件

4.2.1局部荷载加载方式和位置

进行桥面加载时考虑八车道布载，汽车轴重和间距参考CJJ 11-2011 《城市桥梁设计规范》。将荷载布置在跨中，且只布置单排轴重荷载。计算时，取轴重为80 kN，车轮着地宽度×长度=0.6 m×0.25 m，然后将轴重换算为面均布压力施加在模型上。模型划分网格前需要将加载区域对应划分出来。计算模型的布载示意见图7。

图7 布载位置

4.2.2边界条件和其他荷载

本节中的局部模型，一个为主梁截面约束竖向位移和纵桥向位移，另一个为主梁截面约束竖向位移和横桥向位移。其他荷载仅考虑自重。

4.3 计算结果

选取荷载施加处截面B和截面A，作为提取应力结果的代表截面。截面A和B的相对位置见图8，其应力分布结果分别见图9、图10。

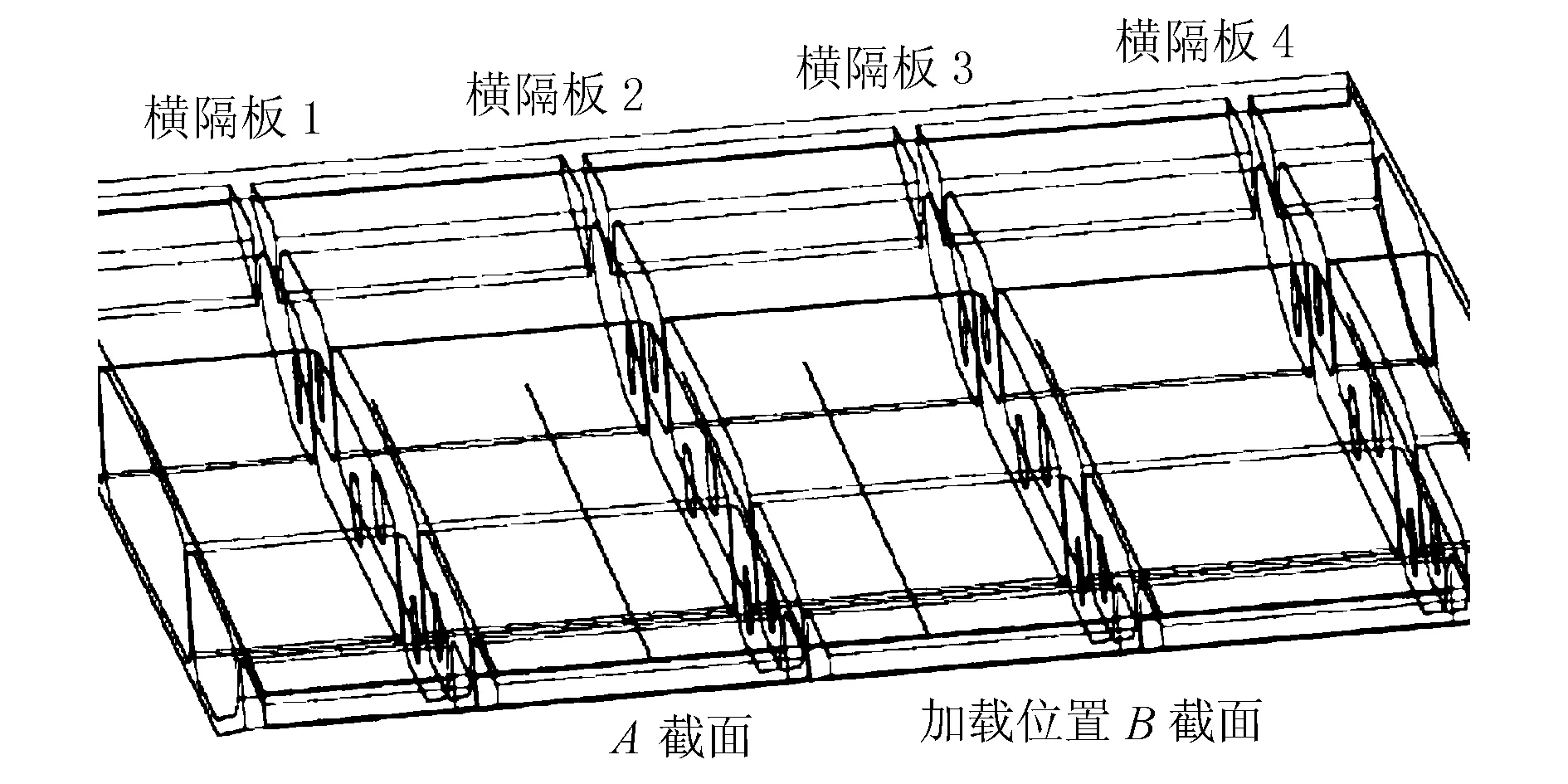
图8 截面位置及编号示意

图9 截面A正应力(单位：MPa)

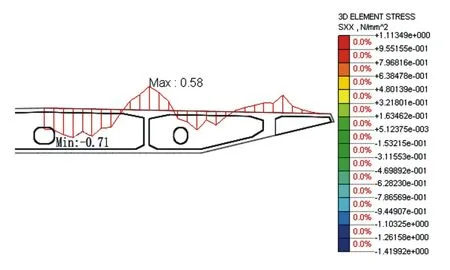
图10 截面B正应力(单位：MPa)

由图9、图10可知，当在截取的局部模型的跨中加载时，箱梁不同截面存在不同程度的剪力滞效应；截面正应力在腹板处达到峰值，由该腹板向其两侧逐渐减小，在与其相邻的腹板之间的中间位置附近达到反向峰值。靠近加载位置的截面B，剪力滞效应更为明显，其最大正应力为0.58 MPa，为拉应力，而其最小正应力为-0.71 MPa，为压应力，2个峰值正应力的差值达到了1.29 MPa，正应力变化相对较为剧烈，分布较为不均匀；而远离加载位置的截面A，剪力滞效应虽然也存在，但其最大正应力为0.25 MPa(是截面B相应应力的43%)，为拉应力，其最小正应力为-0.28 MPa(是截面B相应应力的39%)，为压应力，2个峰值正应力的差值只有0.53 MPa(是截面B相应应力峰值差值的41%)，正应力变化相对截面B来说较为平缓，正应力分布较为均匀。

因此，对于箱梁来说，其横断面最不利受力位置位于腹板和相邻腹板间跨中附近。在应力较大的腹板位置，可以通过适当改变腹板和顶板的倒角尺寸，来改变此处的应力状态；对于相邻腹板间跨中位置的应力，可以通过适当减小腹板间距来改善其应力状态，还可以根据行车道的横向布置，合理设计箱梁横断面，优化腹板的横向位置，使行车道恰好位于腹板附近，以改善应力状态。

5 结论

1) 应尽量避免塔梁结合段的尺寸突变，增加尺寸过渡，以减少应力集中。在主梁位置，拉、压应力都在正常范围内，较大应力值主要集中在塔梁结合处的主梁悬臂端部，对箱梁中部位置影响较小；对于主塔，应力的突变及不均匀分布主要集中在塔梁结合位置的较小区域内，故这些区域应注意几何构造的合理性并适当加强配筋设计。

2) 箱梁的剪力滞效应较为明显，截面正应力在腹板处达到峰值，由该腹板向其两侧逐渐减小，在与其相邻的腹板之间的中间位置附近达到反向峰值。靠近加载位置的截面，最大正应力和最大负应力的差值较大，应力分布更为不均匀，剪力滞效应更为明显；当截面远离加载位置时，截面的正、负应力的最值差值较加载附近截面的更小，且应力分布更加平缓。

3) 对于箱梁而言，其横断面最不利受力位置位于腹板和相邻腹板间跨中附近。在应力较大的腹板位置，可以通过适当改变腹板和顶板的倒角尺寸，来改变此处的应力状态；对于相邻腹板间跨中位置的应力，可以通过适当减小腹板间距来改善其应力状态，还可以根据行车道的横向布置，合理设计箱梁横断面，优化腹板的横向位置，使行车道恰好位于腹板附近，以改善应力状态。