软土地基单桩桩周土固结解及影响因素研究

牛 顺 郭 昊

(1.广西大学土木建筑工程学院 南宁 530004； 2.中铁二十局集团第四工程有限公司 青岛 266100)

静压桩施工工艺由于质量稳定、造价低、振动小，以及承载力高等优点在软土地区基础建设中得到了广泛应用。然而相比于钻孔灌注桩，静压桩施工过程中会产生挤土效应，对邻近桩和构筑物造成不良影响。在饱和软黏土地基中，沉桩过程会产生很大的超静孔隙水压力，过大的超静孔隙水压力会妨碍施工速度，加剧挤土效应的不良影响。随后，人们在工程实践中发现，静压桩沉入土中之后，单桩承载力会随着时间的推移，有逐渐增加并且最后趋于稳定值的现象。在沉桩过程中，会引起超静孔隙水压力急剧增加，但是随着时间的推移，土中的孔隙水压力会逐渐消散，土体开始固结，有效应力增加，桩的承载力增加[1-3]。

针对静压桩沉桩引起的桩周土体超静孔隙水压力的变化，国内外已有许多的研究成果。确定出沉桩引起的超静孔隙水压力大小、分布规律及其消散情况，对于解决实际工程问题具有重要意义。静压桩承载力时效性与超静孔压的消散相关，因此展开了针对桩周土固结的研究，桩周土固结主要从固结控制方程、初始条件和土体参数出发。Randolph等[4]利用一个类似于Biot固结理论的方式，得出了平面应变情况下孔压沿径向消散的控制方程，该解答可得出土体中任意时刻和任意位置处的孔隙水压力大小，并得到土体固结度。赵明华等[5]结合圆孔扩张理论，将土体视为弹性介质，建立固结控制方程，并提出了沿径向的分布函数。姚文娟等[6]考虑了土体径向和竖向的孔压消散，利用轴对称控制方程对桩周土的固结进行了分析。

大量研究表明，合理建立固结控制方程，选择合适的求解方法，对准确求解问题至关重要。在前人研究的基础上，本文从理论出发，推导出软土地基中桩周土固结半解析解，并对控制方程进行量纲一的量化处理，将得到的解答与高子坤等[7]的解答进行对比验证。同时，利用数值分析方法探究土体物理参数和桩身几何参数对土体固结速率的影响。

1 数学模型

1.1 问题

在饱和软土的沉桩结束后，桩周土体的固结计算模型见图1。

H-桩在地基土中的贯入深度，m；rd-静压桩的外径，m；kr、kv-土的水平渗透系数、竖向渗透系数，m/s；u|t=0=f(r,z)-土体中的超静孔压,Pa。

1.2 基本假定

1) 在土体固结的空间轴对称问题下，对于单桩问题，假设桩身为圆柱形。

2) 桩土作用边界为径向隔水边界，桩底部土体为不排水边界，桩顶部地面为自由排水面。

3) 压桩过程假设为平面应变问题，仅考虑压桩后的固结变化，即视为瞬时沉桩。

1.3 固结控制方程

沉桩结束后，桩周土中的超静孔压会沿着径向和竖向消散，参考Randolph等[4]关于饱和软土沉桩问题的研究，桩周土体固结控制方程为沉桩过程可假设为平面应变的问题，故静压桩桩周土的固结控制方程为

(1)

式中：u为土体中产生的超静孔压，Pa；z为土体任一点距离土体表面的深度，m；r为土体径向任一点到桩中心点的距离，m；Cr和Cv分别为水平固结系数和竖向固结系数，m2/s；t为时间，s。

1.4 初始条件

沉桩过程主要是桩身与桩侧土体发生置换，桩底部土体的应力变化类似球体膨胀问题，而沿着桩身竖向呈现圆柱形膨胀。本文假定沉桩产生的初始孔压分布范围为孔压影响区re，且初始孔压沿水平方向呈对数衰减，沿深度方向线性增加，根据文献[2]的研究，桩周超静孔隙水压力的分布规律，即桩周土固结初始条件为

(2)

式中

其中

γ′为土体有效重度；n′为压桩造成的超静孔隙水压力的影响半径系数。根据唐世栋等[8]的研究，挤土贯入桩超静孔压分布范围一般约为20倍桩半径(rd)，故本文影响区半径取re=20rd；μ、E、cu和ca分别为土的泊松比、弹性模量、黏聚力和不排水抗剪强度；φ和A分别为桩土界面处的内摩擦角和Skempton孔隙压力系数。

记t=0时，压桩结束后在桩端r=rd、z=H处产生的最大超静孔隙水压力值为

u0=u(rd,H,t)|t=0=(b0+c0H)lnn′

(3)

1.5 边界条件

对于水平边界条件，当与桩中心径向距离r到达影响区范围时，土体的超静孔压大小可忽略不计。

水平边界条件为

(4)

竖向边界条件为

(5)

2 求解

2.1 方程量纲一的量化

为了便于求解及敏感性分析，定义了如下量纲一的量化参数。

(6)

式中：u0=u(rd,H,t)|t=0=(b0+c0H)lnn′，下标D为量纲一的量化项。

固结控制方程可简化为

(7)

式中：η′=H/rd；κ=kr/kv。

初始条件为

(8)

边界条件为

(9)

2.2 超静孔压解答

根据初始条件(8)，对控制方程(7)及边界条件(9)关于变量Tv进行Laplace变换，得控制方程为

(10)

初始条件为

(11)

边界条件为

(12)

根据边界条件对控制方程作有限Fourier正弦变换见式(13)。

(13)

式中：sin (γnZ)为特征函数；γn为特征值，满足γn=(2n-1)π/2；范数N(γn)满足1/N(γn)=2，得控制方程为。

(14)

其中

径向边界条件见式(15)。

(15)

J0，J1为0阶和1阶第一类柱贝塞尔函数，Y0，Y1为0阶和1阶第二类柱贝塞尔函数。根据径向边界条件式(15)解控制方程式(14)得

(16)

式中

(17)

2.3 地基整体平均固结度解答

对地基土固结解答式(16)进行有限Fourier正弦逆变换，可得量纲一的量超静孔压在Laplace域内的解答见式(18)。

由Laplace域内地基上量纲一的量的超静定孔压解答，求得Laplace域内地基土平均固结度计算方法见(19)。

(19)

其中

最后通过Laplace逆变换数值算法可得到时域内地基量纲-的量超静孔压解答。

3 算例及对比验证

3.1 算例验证

根据文献[1]的相关研究，浙江省某电厂的试桩为一根45 cm×45 cm的预制混凝土方桩，入土深度30.9 m。在打桩后第10，19，31，61，91 d 各进行1次桩基承载力试验。

取第91 d的测量承载力值，估算桩的最终承载力，可得实测承载力值和由承载力值换算得到的等效固结度值，见表1。

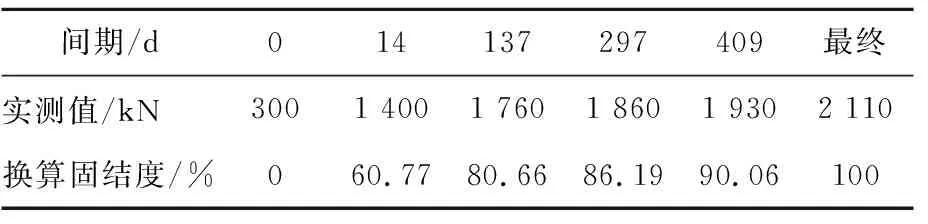
表1 实测承载力和等效固结度

将上述参数代入式(17)、式(21)，其计算结果与等效固结度的对比见图2。由图2可见，二者的结果基本吻合，说明了解答的正确性。

图2 换算固结度与解析固结度

3.2 对比验证

文献[7]根据土体固结的空间轴对称问题，建立了桩周土体固结模型，利用分离变量法推导出压桩影响区平均固结度的级数解，并计算了不同地基土条件下管桩压桩后地基土固结情况。由于文献未进行无量纲化处理，本文按照文献中参数进行设置，并将固结度U与时间因子Tv的关系转换成固结度U和时间t的关系。将本文的解答与文献[7]的解答进行对比，绘图见图3。由图3可知，两者结果具有较好的一致性，进一步验证了解答的合理性。

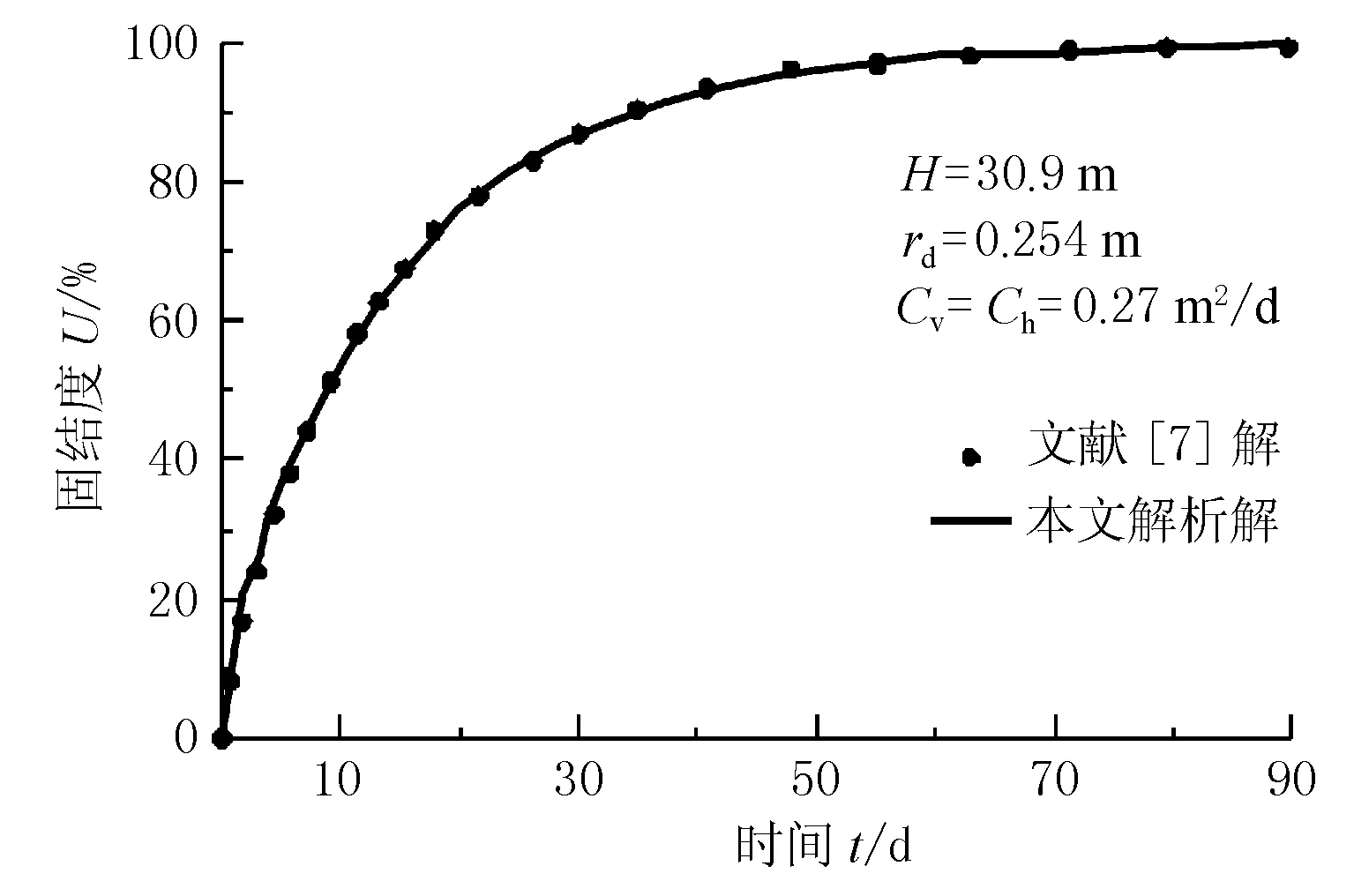
图3 本文解与文献[7]解答的对比

4 固结敏感性分析

为方便求解固结问题和分析固结特性，本文在对固结模型求解时进行了无量纲化处理。从文中固结控制方程和边界条件中不难发现，对桩周土固结产生影响的参数有：①桩周土体物理参数即渗透系数比κ。②桩身几何参数即桩的长径比η。

根据地基规范手册[9-10]给出的土体物理参数取值的参考范围可知：对于饱和软黏土，一般情况下径向渗透系数大于竖向渗透系数，故κ在1～15范围取值。根据实际过程中管桩常见的几何尺寸和压桩深度，文中桩身几何参数η的取值范围为60～180。

4.1 土体物理参数影响分析——渗透系数比κ

土体水平-竖向渗透系数比对土体固结度的影响曲线图见图4。

图4 不同渗透系数比对桩周土固结的影响

由图4可见，随着κ的不断增大，土体固结曲线逐渐向左移动，达到同一固结度所需要的时间逐渐变短，土体的固结速度明显提高，达到相同固结度所需时间明显减小，地基土中的超静孔隙水压力消散速度显著提高，这是由于土体水平方向的透水能力增强而加速了土体超静孔压的消散速度。此外，由图4还可以看出，当κ>9时，土体的固结度曲线向左移动的幅度逐渐减小，即水平渗透系数的增大对固结度的提高是有限的，说明土体固结的能力不仅受渗透系数的影响，还受土体其它几何及物理参数影响。

4.2 桩身几何参数影响分析——桩的长径比

由于在实际工程中，桩的几何尺寸都是不一样的，桩的外形尺寸会对初始超孔隙水压力的大小和范围产生影响。因此，有必要探究不同桩身几何参数对土体固结特性的影响。

当桩长等其他参数不变时，桩的长径比η分别取60，90，120，150，180时的固结曲线图见图5。结果表明：在其它参数均相同的前提下，长径比越大，桩周土的固结曲线不断向左移动，达到同一固结度所需时间在逐渐缩短，地基土固结速率随之提升，如当时间因子为10-2时，长径比为180条件下的固结度比长径比60时提高了约70%，这说明桩的几何尺寸同样是影响桩周土固结速率的重要因素。

图5 桩长径比对桩周土固结的影响

6 结语

本文通过对控制方程进行量纲一的量化处理，求解软土地基中桩周土体的固结问题，得到了桩周土固结半解析解，并且将该解答与算例及文献解析解进行对比，验证了本解答的正确性。同时，利用数值分析方法研究了土体物理参数和桩身几何参数对土体固结速率的影响，得出以下主要结论。

1) 通过将解答进行对比验证，表明了该解答具有的合理性与准确性。

2) 土体水平渗透系数增大，土体固结速率随之提高。当κ>9时，土体的固结度曲线向左移动的幅度逐渐减小，说明土体固结的能力不仅受渗透系数的影响，还受土体其它几何及物理参数影响。

3) 随着桩的长径比η增大，土体固结速率随之提高。长径比为180条件下的固结度比长径比60时提高了约70%，说明桩的几何尺寸同样是影响桩周土固结速率的重要因素。

4) 其他参数不变，随着渗透系数比值增大，桩周土的固结速率增快趋势在减弱。由此可知，影响地基土固结的因素并不是单一的，应综合考虑。

此外，对于桩身几何尺寸的研究本文只考虑了圆形管桩长径比对固结的影响，其他情况下，如桩的壁厚及桩不同的截面形状等情况下的固结速率变化，有待进一步研究。