散体材料桩复合地基桩土应力比计算方法研究
田 莉,韩冉冉
(交通运输部天津水运工程科学研究所 港口水工建筑技术国家工程实验室 水工构造物检测、诊断与加固技术交通行业重点实验室,天津 300456)
散体材料桩复合地基作为一种行之有效的地基处理方式,在土建、交通、港口等工程领域已经得到大规模的应用,并取得了较好的效果。为能进一步指导施工,推动技术的发展,国内外学者对散体材料桩复合地基进行了较为深入的研究。从国内学者的研究内容看,主要集中在以下几个方面:散体材料桩复合地基桩土应力比问题[1-2]、固结问题与变形问题[3-4]、承载力问题[5-6]等几个方面。主要通过现场试验[7-10]、室内试验[11]和理论计算[12-14]等手段进行研究。由于在进行散体材料桩复合地基固结变形、承载力等问题的研究时,要考虑桩土应力比的影响,使得散体材料桩桩土应力比问题逐渐成为研究的热门问题,同时也成为解决其他问题的关键问题。但由于散体材料桩-土相互作用的机理复杂,影响因素较多,未能得到较为完善的桩土应力比解答。

图1 桩与桩周土应力应变关系示意图Fig.1 Stress-strain of pile and soil
本文以圆孔扩张理论为基础,在假定桩-土竖向变形相等的前提下,考虑桩-土侧向变形协调及应力平衡,给出散体材料桩土应力比的理论计算公式。并在此基础上分析了公式中各参数对桩土应力比的影响。
1 散体材料桩土应力比计算公式
1.1 基本假定
散体材料桩在侧向土的约束下,随着竖向压力的增大,桩体发生侧向膨胀,通过应力调整获得更大的侧向约束力,如图1所示。针对散体材料桩与桩周土的受力特点,作基本假定如下:(1)散体材料桩与桩周土符合完全弹性、均匀性、各向同性和连续性条件;(2)散体材料桩与桩周土竖向变形相等;(3)散体材料桩与桩周土分界面上满足变形协调条件和正应力平衡方程;(4)散体材料桩与桩周土径向应力增量沿深度均匀分布;(5)不考虑自重影响。
1.2 计算公式推导
设散体材料桩复合地基上部作用均布压力q,桩与桩周土的弹性模量分别为Ep、Es,泊松比分别为νp,νs,置换率为m。根据广义虎克定律,桩与桩周土分别满足轴对称条件下的物理方程
(1)
式中:εr、εθ、εz分别为径向应变、切向应变和竖向应变;σr、σθ、σz分别为径向正应力、切向正应力和竖向正应力;E为弹性模量;ν为泊松比。
在竖向桩与桩周土变形相等
εzp=εzs
(2)
式中:εzp、εzs为散体材料桩与桩周土竖向应变。
根据圆孔扩张理论,桩体受均布外压时径向正应力与切向正应力相等
σrp=σθpσrs=σθs
(3)
式中:σrp、σθp分别为散体材料桩径向正应力、切向正应力,σrs、σθs分别为桩周土径向正应力、切向正应力。
在不考虑桩-土时效特性的前提下,散体材料桩及桩周土分界面上满足应力平衡方程
σrp=σrsσθp=σθs
(4)
在平面内桩体膨胀的量等于桩间土压缩量[1],即在桩-土分界面上满足变形协调条件
(5)
式中:εrp、εθp分别为散体材料桩径向应变、切向应变;εrs、εθs桩周土桩径向应变、切向应变;m为置换率。
利用(1)~(5)式可得
(6)
Es(σzp-2νpσrp)=Ep(σzs-2νsσrp)
(7)
式中:Ep,σzp,νp分别为散体材料桩弹性模量、竖向正应力和泊松比;Es,σzs,νs分别为桩周土弹性模量、竖向正应力和泊松比。
由(6)和(7)可得
(8)
(9)
令Kn=Ep/Es,n=σzp/σzs代入(8)和(9)可得
(10)
(11)
式中:Kn为桩-土弹性模量比;n为桩土应力比。
将n带回式(8),并令n′=σzp/σrp得
(12)
式中:n′为桩竖向-侧向应力比。
将(11)代入(12)得
(13)
通过上面的推导可以看出,散体材料桩复合地基桩土应力比公式由桩-土弹性模量比、桩泊松比,桩周土泊松比及置换率等4个参数控制,而桩竖向-侧向应力比同样由这4个参数控制。
2 散体材料桩土应力比影响因素分析
散体材料桩复合地基桩-土应力受多方面因素的影响[2],且由于桩土相互作用的复杂性及时效性,在整个施工加载过程中不断的调整,难以得到精确的研究。为此,本节将结合散体材料桩土应力比公式,探讨4个控制参数对桩土应力比的影响。为便于对散体材料桩-土应力进行分析,先进行单因素分析,然后再根据实际工程中可能遇见的情况进行多因素分析。
2.1 弹性模量比对桩土应力比的影响
根据相关文献,当桩周土的弹性模量小时,桩土应力比取高值。但由于相关理论的研究相对不足,至今未能得到桩土应力比与弹性模量比之间的理论解答。
图2为根据本文桩土应力比公式得到的桩土应力比与弹性模量比之间的关系曲线。从图中可以看出:在置换率、桩的泊松比及桩间土泊松比均不变时,桩土应力比与桩-土弹性模量比之间的关系曲线为一单调递增曲线,说明桩土应力比随桩-土弹性模量比的增大而增大。通常情况下,桩-土弹性模量比的范围为5~10,而曲线中与之对应的桩土应力比范围为2.6~4.7,这与规范中的经验取值较为接近。由于目前散体材料桩成桩工艺的问题,在大多数情况下桩体的变形模量小于30 MPa,这对于变形模量大的桩周土较为不利,由于两者的比值较小,其桩土应力比也较小,相应的加固效果不理想,如文献[13]指出对于变形模量大于8.0 MPa的桩周土,采用碎石桩加固效果不佳。
2.2 桩的泊松比对桩土应力比的影响
虽然桩的泊松比在以往文献桩土应力比公式中得到了体现,但根据目前的研究现状,桩的泊松比对桩土应力比的影响却在文献中提及较少。
图3为桩的泊松比随桩土应力比变化曲线。为便于分析,采用与图2相同的置换率和桩周土泊松比。从图中可知:桩土应力比随桩的泊松比变化曲线呈微凹状,桩土应力比随着桩泊松比的增大而减小。就变化量而言两者较为接近,桩的泊松比增长量为0.16,对应的桩土应力比减小量为0.12;但从变化率的角度看,桩的泊松比变化率(Δνp/νp)为107%,而对应的桩土应力比的变化率(Δn/n)为3%。这说明在其它条件不变的情况下,桩的泊松比对桩土应力比的影响很小。
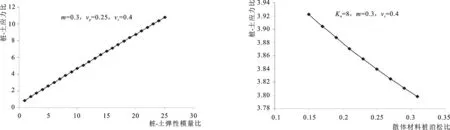

图2 n-Kn关系曲线Fig.2 Relation curve of n-Kn图3 n-νp关系曲线Fig.3 Relation curve of n-νp
2.3 桩周土泊松比对桩土应力比的影响
在一般情况下,土的泊松比越大,则土的静止侧压力系数越大。从这个意义上讲,如果桩周土未达到塑性破坏,在承受同样上部荷载的情况下,桩周土的泊松比越大,产生的侧向力越大,则对散体材料桩的约束作用越明显。

图4 n-νs关系曲线Fig.4 Relation curve of n-νs
从图4桩周土的泊松比随桩土应力比变化曲线可知:桩土应力比随桩周土的泊松比变化曲线呈微凸状,桩土应力比随着桩周土泊松比的增大而减小。桩周土泊松比为0.3时,对应的桩土应力比为5.8;桩周土泊松比为0.46时,对应的桩土应力比为2.2。桩周土泊松比增长量为0.16,而对应的桩土应力比减小量为3.6;从变化率的角度看,桩周土泊松比变化率(Δνs/νs)为53%,而对应的桩土应力比的变化率(Δn/n)为62%。这说明在其他条件不变的情况下,桩周土泊松比的变化对桩土应力比影响显著。
2.4 置换率对桩土应力比的影响

图5 n-m关系曲线Fig.5 Relation curve of n-m
根据有关文献及工程经验,散体材料桩土应力比随着置换率的增大而减小,这是定性的描述,而对桩土应力比随置换率变化的定量描述的研究则较少。下面将结合图5对桩土应力比随置换率的变化进行定量的描述。
由图5可知,散体材料桩土应力比随着置换率的增大而减小,且呈微凸状。从两者的变化量来看较为接近,置换率从0.05增长到0.45,增加了0.4;而桩土应力比从4.0减小到3.7,减小了0.3,从两者的变化率来看,置换率的变化率(Δm/m)为800%,而桩土应力比的变化率仅为8%。这说明在其他条件不变的情况下,置换率对桩土应力比的影响甚微。因此,在实际工程中,仅仅通过改变置换率对桩土应力比进行调整,是难以达到预期效果的。
2.5 桩土应力比多因素分析
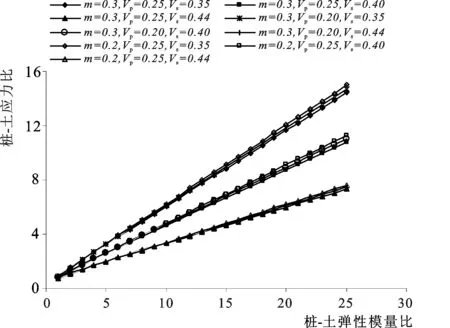
图6 不同工况下n-Kn关系曲线Fig.6 n-Kn curve under different conditions
单因素分析能够获取其中的重点影响因素,却不利于工程应用,因此根据4个参数对桩土应力比的影响大小,进行多参数分析,以便于工程应用。

图6为不同工况下桩周土泊松比下桩土应力比与弹性模量比的关系曲线。由图可知:当置换率为0.3,桩体泊松比为0.25,桩周土泊松比为0.35,桩-土弹性模量比为25,桩土应力比为14.4;而当置换率为0.3,桩体泊松比为0.25,桩周土泊松比为0.44,桩-土弹性模量比为25,桩土应力比仅为7.3。这说明桩周土泊松比增大,明显减弱了桩-土弹性模量比对桩土应力比的影响。同时说明在实际工程中采用相同工艺和置换率的散体材料桩,在砂性土中将获得更大的桩土应力比,可以获得更好的加固效果。当置换率为0.3,桩体泊松比为0.20,桩周土泊松比为0.44,桩-土弹性模量比为25,桩土应力比为7.5,比同条件下桩体泊松比为0.35时提高0.2。这说明在不改变置换率、土质性质及桩-土弹性模量比相同的条件下,桩体材料泊松比对桩土应力比影响很小。当置换率为0.2,桩体泊松比为0.25,桩周土泊松比为0.44,桩-土弹性模量比为25,桩土应力比仅为7.6,比同条件下置换率为0.3时提高0.3。这说明在不桩体材料性质、土质性质及桩-土弹性模量比相同的条件下,置换率比对桩土应力比影响不明显。 综上分析,可以看出在桩-土弹性模量比、桩泊松比,桩周土泊松比及置换率4个参数中, 桩-土弹性模量比、桩泊松比是影响桩土应力比的关键因素。此外,对比图6中个各工况曲线,可以看出在各种参数组合工况下桩土应力比均随弹性模量比均呈现线性单调递增特点,而其他3个参数的影响均体现在对n-Kn关系曲线的斜率上,即桩周土泊松比、桩体泊松比、置换率增大,n-Kn关系曲线的斜率均减小。
3 散体材料桩竖向-侧向应力比分析
由图7和图8可知,桩竖向-侧向应力比受置换率及桩的泊松比的影响较小,且随两者呈单调递减趋势,这与桩土应力比随置换率及桩的泊松比的变化规律相似。
由图9和图10可知,桩-土弹性模量比和桩周土泊松比对桩竖向-侧向应力比的影响显著。桩竖向-侧向应力比随桩-土弹性模量比呈线性增长趋势。桩竖向-侧向应力比随桩周土泊松比的变化曲线呈微凹状单调递减趋势,这与桩周土泊松比对桩土应力比的影响稍有不同。将图9和图10与前文图2和图4对比发现,桩-土弹性模量比和桩周土泊松比对桩竖向-侧向应力比的影响大于对桩土应力比的影响,尤其是桩周土泊松比对桩竖向-侧向应力比的影响更为显著。
此外,当桩竖向-侧向应力比达到一定数值,桩体内大小主应力将达到极限平衡状态,此时的桩土应力比将达到最大值。因此,在进行桩土应力比计算时,为保证桩土应力比计算的合理性,应先对桩竖向-侧向应力比进行分析。
4 工程应用
为验证本文方法的可行性和实用性,现以大连某填海造陆工程振冲碎石桩地基处理工程为例进行说明,本工程加固区以不排水强度小于20.0 kPa淤泥质土为主,厚度10.0 m。其主要计算参数见表1。
根据前文桩土弹性模量比定义可知本工程实例Kn=7.5,通过(11)式计算得到桩土应力比n=3.17,而现场实测桩土应力比n=3.01,两者偏差5.3%,计算值与实测值较为接近,满足工程需要。为判别桩体是否处于破坏状态,当在荷载作用下碎石桩桩体处于极限平衡状态时,根据经验及相关规范取碎石桩桩体的内摩擦角为40°,此时桩体内大小主应力比为4.60,这相当于限定了碎石桩竖向-侧向应力比n′的极限值。同时根据式(13)计算得桩竖向-侧向应力比n′=4.24,该值小于桩体处于极限平衡时桩体内大小主应力比(桩体未出现鼓胀破坏),进而判定式(11)计算的结果是合理的。
5 结语
(1)基于圆孔扩张理论和理想弹性体的基本假定,在考虑散体材料桩-土相互作用的前提下,假定桩-土竖向变形相等,并根据桩-土在侧向分界面上满足变形协调条件和应力平衡方程,导出了散体材料桩土应力比计算公式,并在此基础上给出了桩竖向-侧向应力比公式。
(2)引入了新参数桩-土弹性模量比Kn,对散体材料桩土应力比影响因素进行了分析,并从理论上找到了影响桩-土应力的关键因素。桩-土弹性模量比和桩周土泊松比是影响桩土应力比的关键因素,而置换率对桩土应力比的影响最小。
(3)引入桩竖向-侧向应力比参数n′,可以判断桩体是否达到塑性破坏状态,用以辅助分析桩土应力比计算结果的合理性。换言之,合理桩土应力比的存在条件要以桩体未出现破坏为前提。
(4)结合工程实例,对桩土应力比理论计算值和实测值进行了对比,并通过引入桩竖向-侧向应力比判定桩土应力比的合理性,结果表明理论计算值和实测值差别较小,满足工程需要。

