刚性基础下砼芯水泥土桩复合地基沉降计算
俞建霖,徐山岱,杨晓萌,陈张鹏,龚晓南
(1.浙江大学滨海和城市岩土工程研究中心,浙江杭州,310058;2.浙江省城市地下空间开发工程技术研究中心,浙江杭州,310058)
随着工程建设对软土地基承载力和沉降要求的不断提高,各种地基处理技术不断发展涌现。传统的水泥搅拌桩存在桩身强度低和承载力小的缺点;混凝土桩承载力高,但作为摩擦桩使用时提供的侧摩阻力小,当桩周土的承载力达到极限时,桩身强度未完全发挥,浪费桩身材料。砼芯水泥土桩通过在水泥搅拌桩中插入预制砼芯,利用水泥搅拌桩较大的比表面积提高侧摩阻力,同时利用高强度的砼芯承担上部荷载,充分发挥2种桩型的优势,从而有效地提高承载力,减小沉降量,具有较好的经济性。根据砼芯和水泥搅拌桩桩长的差异,可分为短芯、等芯和长芯桩。目前国内外诸多学者通过现场足尺试验、室内模型实验、数值分析和理论解析法研究砼芯水泥土桩作为桩基础的荷载传递机理和变形特性[1-6],但对砼芯水泥土桩作为复合地基中增强体的工作性状研究成果较少。鲍鹏等[7]采用数值分析方法研究了复合地基中砼芯的桩身应力、位移以及砼芯长度和含芯率对极限承载力的影响;JAMSAWANG等[8]采用室内试验和数值分析方法研究了砼芯与水泥土桩界面的工作特性以及砼芯长度对桩体承载力和沉降的影响规律;洪波[9]基于等截面模量的概念,提出了一种砼芯水泥土桩复合地基的沉降计算方法;李俊才等[10]根据现场静载试验及有限元计算结果,分析了复合地基中砼芯、水泥土桩和桩周土的荷载分担比,研究了地表处应力分布以及砼芯轴力随深度的变化规律;王驰等[11]探讨了不同芯长比和含芯率条件下砼芯水泥土桩复合地基的荷载传递机理和沉降变化规律;叶观宝等[12]推导了刚性基础下砼芯水泥土桩复合地基桩土应力比的计算公式,并分析了砼芯直径和桩长以及水泥土桩桩长的影响;徐礼阁等[13]基于荷载传递法推导了层状地基中桩身-水泥土-土体相互耦合作用的静钻根植桩单桩沉降计算公式;张振等[14]通过室内模型试验,研究了短芯劲芯水泥土桩承载路堤失稳破坏模式,综合分析了桩体渐进式破坏模式和路堤整体失稳规律。对于砼芯水泥土桩而言,砼芯、水泥土桩和桩周土三者之间的界面摩擦特性是影响荷载传递规律的重要因素。大量实测试验结果表明,桩侧摩阻力的发挥与桩土接触面上相对位移有关[15]。彭涛等[16]通过直剪试验研究了水泥土-混凝土界面特性,发现二者之间的界面剪切应力与位移有着密切关系,前期近似呈线性增长,峰值过后缓慢降低。但现有的理论解析法大多假定水泥土桩与桩周土之间的侧摩阻力完全发挥,认为砼芯和水泥土桩之间不发生相对位移,采用桩体复合模量或侧摩阻力沿深度不变来进行分析,未考虑界面相对位移对侧摩阻力的影响。本文在前人基础上,针对砼芯和水泥土桩长度相等的等芯长桩,考虑砼芯、水泥土桩和桩周土三者之间的相互作用和变形特性,基于理想弹塑性荷载传递函数,采用荷载传递法,提出一种在刚性基础下计算砼芯水泥土桩复合地基沉降的理论解析法并研究复合地基沉降的影响因素及变化规律。
1 沉降计算方法
1.1 研究对象
图1所示为砼芯水泥土桩布置图。由图1可见:研究对象是由刚性基础下单桩有效处理范围内的复合地基(包括砼芯、水泥土桩和地基土体)所形成的典型单元体。根据典型单元体对称性,典型单元体侧表面上剪力为零。在荷载的作用下,桩周土、水泥土桩和砼芯都会发生压缩。由于三者的弹性模量呈数量级差异,因此,产生的压缩量各不相同。但在刚性基础下三者顶面的沉降一致,势必导致三者之间的砼芯-水泥土桩和水泥土桩-桩周土界面出现相对位移。
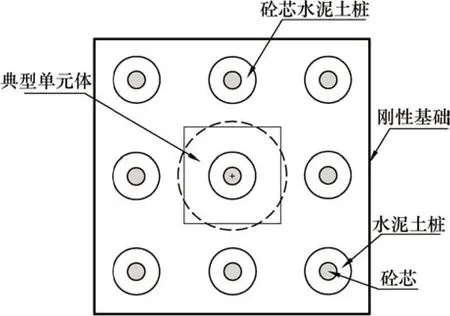
图1 砼芯水泥土桩布置图Fig.1 Sketch for the concrete-cored DCM pile arrangement
图2所示为复合地基变形前后示意图。由图2可见:水泥土桩相对于桩周土产生向下的相对位移,砼芯相对于水泥土桩产生向下的相对位移,因此,在2个界面产生正摩擦力,从而引起三者之间的荷载传递;同时,在桩端平面上,水泥土桩和砼芯分别产生向下的刺入变形,且后者大于前者。
1.2 基本假设
1)水泥土桩、砼芯及桩周土为各向同性线弹性体,刚性基础板刚度无穷大。
2)不考虑水泥土桩的径向变形。
3)砼芯、水泥土桩与桩周土均只发生一维压缩,同一水平面上桩间土应力相等。

图2 复合地基变形前后示意图Fig.2 Schematic diagrams of composite foundation before and after deformation
4)桩周土和水泥土桩之间的界面侧摩阻力(以下统称外界面侧摩阻力)与水泥土桩和砼芯之间的界面侧摩阻力(以下统称内界面侧摩阻力)的发挥与界面相对位移有关,且均符合理想弹塑性荷载传递函数假设。荷载传递法通过选择合理的模型和参数,能够较好地反映桩-土相互作用特性。
5)桩端阻力的发挥也符合理想弹塑性模型假设。
1.3 桩与桩间土的分析模型
取桩顶中心为z轴零点,沿着深度向下为正方向。通过分析典型单元体中的桩周土、水泥土桩和砼芯之间相互作用与受力平衡条件,可以得到三者各自的平衡微分方程:

式中:Ws(z),Wm(z)和Wc(z)分别为桩顶至深度z处桩周土、水泥土桩和砼芯的压缩量;U1和U2分别为水泥土桩和砼芯周长;As,Am和Ac分别为单桩有效处理范围内桩周土、水泥土桩和砼芯的截面积;Es,Em和Ec分别为桩周土、水泥土桩和砼芯的弹性模量;τs和τm分别为外界面和内界面侧摩阻力。
根据理想弹塑性荷载传递函数假设,且相对位移用压缩量之差表示,外界面侧摩阻力τs表达式为[17-18]

式中:ks为外界面侧摩阻力发挥刚度系数;τu1为外界面极限侧摩阻力。
内界面侧摩阻力τm表达式为
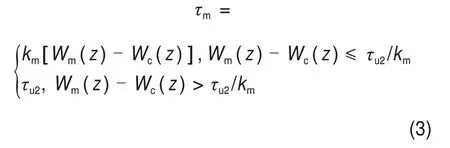
式中:km为内界面侧摩阻力发挥刚度系数;τu2为内界面极限侧摩阻力。
令外界面和内界面侧摩阻力达到极限值的深度分别为h1和h2。由于内界面砼芯与水泥土桩之间的临界相对位移值较小(2~4 mm),在桩体受力过程中相对容易达到[16],因此,可以认为h1>h2。内界面和外界面的极限侧摩阻力τu计算表达式为

式中:β为界面侧摩阻力系数;z为深度;γ为土的天然重度。
根据理想弹塑性模型假设,桩端阻力qp表达式为[17-18]

式中:kp为桩端土刚度系数;qu为极限桩端阻力;qs为桩底土应力;L为桩长;Ws(L)为桩长范围内桩周土的总压缩量;Wp(L)为桩体的总压缩量。Ws(L)与Wp(L)两者差值即为桩端刺入变形。
1.4 方程建立
将式(2)和(3)代入式(1)中可以得到各分段的微分方程表达式。下文中Ws(z),Wm(z)和Wc(z)分别用Ws,Wm和Wc代替。
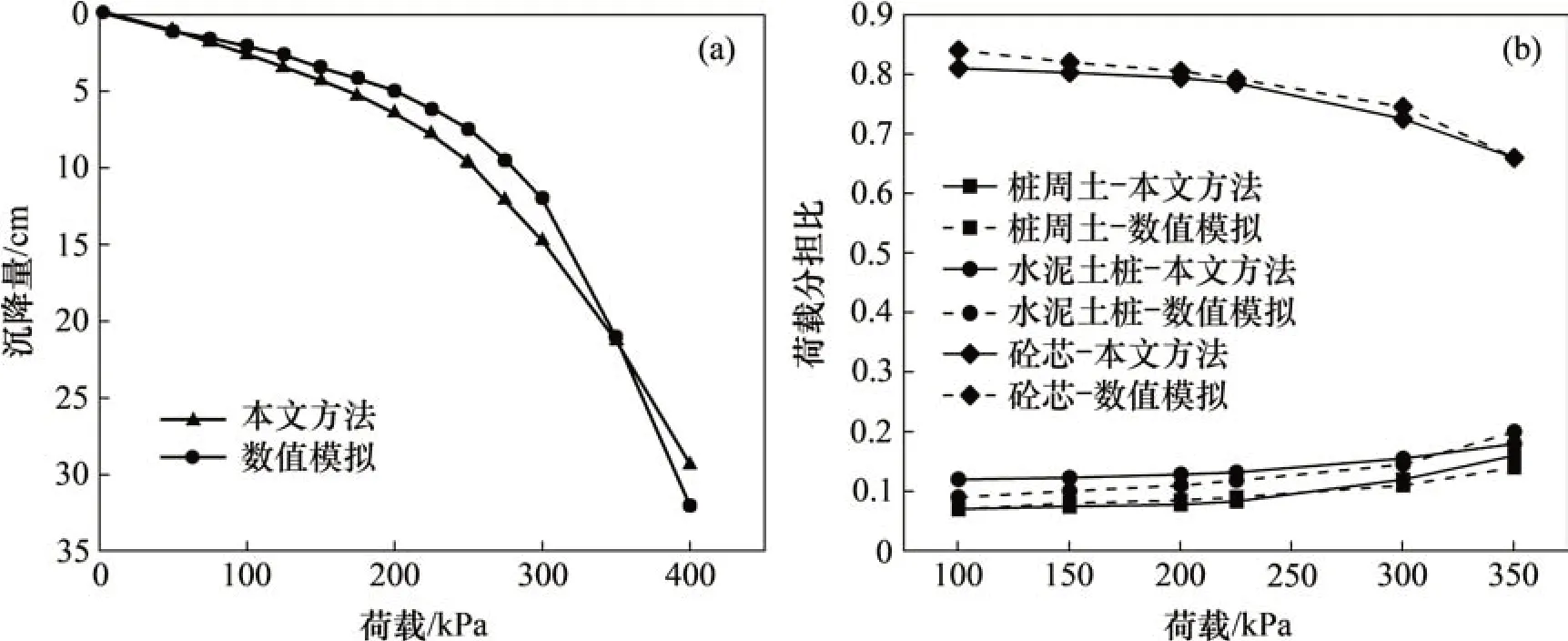
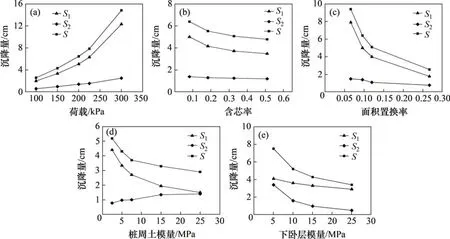
1)当0 求解方程可得到复合地基中桩周土、水泥土桩和砼芯在本段的压缩量Ws1,Wm1和Wc1表达式如下: D1=a1+a2-ma2;D2=a1+a2+na2;Δ=(a1+a2-a3-a4)2+4a2a3;C1,C2,C3,C4,C5和C6为积分常数。 2)当h2≤z 求解方程可得到复合地基中桩周土、水泥土桩和砼芯在本段的压缩量Ws2,Wm2和Wc2表达式如下: 式中:D3=C7,C8,C9,C10,C11和C12为积分常数。 3)当h1≤z≤L时,内界面和外界面侧摩阻力均达到极限值。平衡微分方程如下 求解方程可得到复合地基中桩周土、水泥土桩和砼芯在本段的压缩量Ws3,Wm3和Wc3表达式如下: 式中:C13,C14,C15,C16,C17和C18为积分常数。 1)在基础底面,即z=0 时,复合地基中桩周土、水泥土桩和芯桩相对于基础底面的压缩层厚度为0,故不产生压缩量,且三者承担的荷载之和等于上部荷载F。由此可得: 2)在h1和h2深度处,复合地基中砼芯、水泥土桩和桩周土满足位移和应力连续条件,得到以下12个方程。 在z=h2处, 在z=h1处, 3)在h1和h2深度处,内界面和外界面侧摩阻力达到极限值。由此可得 式中:β1和β2分别为外界面和内界面的侧摩阻力系数。 4)在桩端,即z=L处由式(5)可得 上述方程中有C1,…,C18,h1和h2共20 个未知数,边界条件有式(12)~(31)共20 个。由于直接求解困难,根据文献[17]和[19],采用Wolfram Mathematica 编程求解。将具体参数代入边界条件中,求得h1,h2和积分常数的数值,代入方程Ws(z),Wm(z)和Wc(z)中即可得到复合地基中桩身范围内的桩周土、水泥土桩、砼芯的压缩量。若实际工况是非均质的层状土,则考虑将桩间土的参数采用桩长范围内各土层的加权平均值。 复合地基下卧层沉降计算的关键是下卧层土体附加应力的计算。本文采用Boussinesq-Mindlin联合求解的方法: 1)地表桩间土压力引起的附加应力可由Boussinesq解求得。 2)桩侧阻力和端阻力在下卧层引起的附加应力可由Mindlin解求得。 上述两者迭加后得到下卧层土体附加应力,采用分层总和法就可以计算下卧层土体的沉降量,与桩周土的压缩量相加后就可得到复合地基的总沉降量。 对于外界面,即桩周土-水泥土桩界面,当应力水平较低时,桩侧土处于弹性变形状态,此时可以用弹性解确定桩侧土的刚度系数[20]: 式中:Gs为桩周土体的剪切模量;rm为影响半径;r0为桩身半径;ln(rm/r0)通常可近似取4[21]。 对于内界面,即水泥土桩和砼芯界面,由文献[22]中直剪试验数据可知,内界面侧摩阻力的值与相对位移呈正比,由实验数据反算和文献[12]的建议可以得到km的取值为70~100 MPa/m。 界面极限侧摩阻力采用β法确定,计算公式为 式中:α为修正系数;K为静止土压力系数;φ1为土的内摩擦角。 内界面极限侧摩阻力系数可根据水泥土桩内外界面的水平向受力平衡换算得到β2的计算公式为 式中:D为水泥土桩外径;d为水泥土桩内径;φ2为内界面摩擦角,可根据文献[16]的实验结果取值。 由文献[1]可知,劲性搅拌桩实测侧摩阻力是钻孔灌注桩实测值的1.41~1.62 倍,是勘察报告取值的1.26~1.47倍,因此,取修正系数α=1.4。 RANDOLPH 等[23]基于刚性体压入弹性半空间的解给出了桩端土刚度系数的计算式,将桩顶作用力换成压强[20]得 式中:Gu为桩端土体的剪切模量;υ为桩端土体的泊松比。 通过ABAQUS 软件建模分析并验证本文提出的理论解析法的合理性。数值模拟采用二维轴对称模型,模型两侧受到水平向约束,底部受到水平向和竖直向约束。内界面、外界面和基础底面分别设置接触属性,切向行为采用“罚”公式,分别取摩擦因数为0.4,0.2 和0.3,法向行为采用“硬”接触,接触刚度取2 种介质模量的较小值。在模型尺寸方面,径向长度取20倍水泥土桩半径,竖向取1.5倍桩长,土顶部布设基础板。桩间距为2 m,极限桩端阻力qu为1 000 kPa,km为100 MPa/m。表1所示为水泥土桩、砼芯与基础板材料参数,表2所示为土层参数。 表1 水泥土桩、砼芯与基础板材料参数Table 1 DCM pile and concrete-cored material parameters 表2 土层参数Table 2 Soil parameters 根据表1和表2的具体参数,代入前文已有的解析表达式得到了复合地基的荷载-沉降曲线与桩顶荷载分担比随荷载的变化曲线,最后将数值模拟的结果与本文方法计算得到的结果进行对比验证,结果如图3所示。由图3(a)可见:二者整体变化趋势一致,并且所得的极限承载力也比较接近。由图3(b)可见:1)由于基础刚度大,在上部荷载作用下砼芯承担了大部分荷载,水泥土桩次之,桩周土的荷载分担比最小;2)随着上部荷载增加,砼芯的荷载分担比逐渐减小,桩周土和水泥土桩的荷载分担比逐渐增加。荷载由砼芯向外逐步传递到水泥土桩与桩周土;3)本文方法所得结果与数值模拟结果比较接近。综合分析图3,认为本文提出的砼芯水泥土桩复合地基分析方法是可靠的。 刚性基础下砼芯水泥土桩复合地基总沉降由桩长范围内桩周土压缩量和下卧层压缩量2部分组成。图4所示为复合地基沉降的变化规律及影响因素,计算参数同表1和表2。 图4(a)所示为上部荷载与复合地基沉降的关系曲线。从图4(a)可见:随着荷载增加,沉降量均表现为逐渐增大;当荷载大于225 kPa之后,桩周土压缩量和总沉降量均急剧增大,说明此时复合地基变形进入塑性阶段,变形发展速率加快,此时已达到极限承载力;下卧层沉降量仍未表现出明显的拐点,说明荷载水平的变化对复合地基桩身范围内桩周土压缩量的影响较大。 图3 理论解析法和数值模拟的结果对比Fig.3 Comparison between the results of theoretical analysis and numerical simulation 图4 复合地基沉降的变化规律及影响因素Fig.4 Change regularity and influence factors of composite foundation settlement 图4(b)所示为含芯率与沉降的关系曲线。保持水泥土桩径不变,通过改变砼芯桩径来分析含芯率的影响。由图4(b)可见:随着含芯率增大,桩周土的压缩量逐渐减小,下卧层压缩量略有降低,复合地基总沉降表现为减小;此外,随着含芯率增大,沉降的减小趋势越来越缓,说明含芯率对沉降的控制是有限的。在建设成本一定的条件下,存在最优含芯率,建议取值为0.3。 图4(c)所示为面积置换率与沉降的关系曲线。保持砼芯和水泥土桩的桩径不变,通过改变桩间距来分析面积置换率的影响。由图4(c)可见:随着面积置换率增加,桩周土的压缩量明显减小,下卧层压缩量略有减小。这是因为面积置换率增加导致桩间距降低,在总面积一定的情况下,布桩数增多,提高了复合地基承载力,故复合地基总沉降明显减小,但减小幅度在不断放缓。 图4(d)所示为桩周土压缩模量与沉降的关系曲线。由图4(d)可见:随着桩周土模量增加,桩周土的压缩量明显减小,而下卧层沉降有所增大。这是由于下卧层附加应力有所增长,但复合地基总沉降明显减小,说明桩周土模量主要影响桩长范围内土体的压缩。 图4(e)所示为下卧层压缩模量与沉降的关系曲线。由图4(e)可见:随着下卧层模量增加,下卧层沉降显著减小,但减小趋势逐渐放缓;桩周土的压缩量有所减小,但减小幅度明显比下卧层的小,复合地基总沉降表现为显著减小,说明下卧层模量主要影响下卧层土体的压缩。 1)通过与数值模拟的计算结果进行对比,验证了本文提出的刚性基础下砼芯水泥土桩复合地基沉降计算方法的可靠性,说明该方法具有一定的工程实用性。 2)对于刚性基础下砼芯水泥土桩复合地基,砼芯承担了较大部分的上部荷载,水泥土桩次之,桩周土的荷载分担比最小。随着上部荷载增加,砼芯的荷载分担比逐渐减小,桩周土和水泥土桩的荷载分担比逐渐增加,荷载由砼芯向外逐步传递到水泥土桩与桩周土。 3)复合地基总沉降、桩周土压缩量与含芯率、面积置换率、桩周土和下卧层模量呈负相关,与上部荷载呈正相关。 4)下卧层模量主要影响下卧层沉降且呈负相关发展趋势,而桩周土模量的增长会导致下卧层沉降增大。





1.5 边界条件






1.6 方程求解
1.7 下卧层沉降计算
2 界面模型参数的选取
2.1 界面侧摩阻力发挥刚度系数
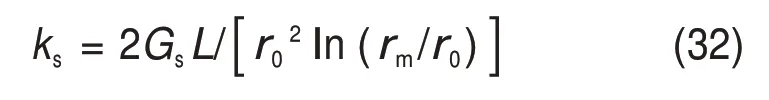
2.2 界面侧摩阻力系数


2.3 桩端土刚度系数
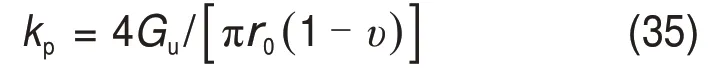
3 数值模拟结果及对比验证


4 复合地基沉降的影响因素
5 结论

