城市轨道交通板式无砟轨道结构摊铺层粗糙表面的构建及评价指标研究

陈宪麦，彭俊，姜晓文，王跃跃，王梦林，刘耀强，郭世豪

(1.中南大学土木工程学院，湖南长沙，410075；2.深圳市城市交通规划设计研究中心有限公司，广东深圳，518035；3.中铁一局集团新运工程有限公司，陕西咸阳，712000)

接触问题在无砟轨道结构中无处不在，但是传统的无砟轨道模型对接触面粗糙度的影响考虑得并不全面。在车辆-轨道耦合动力学中[1]，只考虑轨道随机不平顺对耦合系统的影响。基于商业软件的有限元建模过程[2-3]往往将各个接触面视为完全光滑。但是在实际施工过程中，对接触面的粗糙度有一定要求，而相关规范暂无具体限值要求[4]，或者相关限值理论支撑较不明朗[5]，需要进一步研究。当前，一些学者对车辆-轨道耦合动力学开展了研究。曾庆元等[6-7]提出了弹性总势能不变值原理以及对号入座法则，解决多自由系统的刚度矩阵建立的问题；翟婉明[8]建立了较为完善的车辆-轨道空间动力学模型，并用大量实验验证模型的正确性；雷晓燕[9]建立了车辆-轨道-路基耦合动力学模型，利用有限元方法计算系统的振动响应；高亮等[10]建立了基于有限元软件的桥梁无缝道岔空间耦合模型，并分析了相关工况。关于分形几何，MANDELBORT[11]首先提出分形概念；SAYLES等[12]提出接触表面的形貌变化过程是一种非平稳的状态，表面形貌特征具有随机性和自相似性等特征；BOWDEN[13]等将统计学理论应用到表面接触研究，并建立了一种弹塑性变形模型；GREENWOOD等[14]提出了G-W接触模型，同时符合经典力学和统计学的要求；MAJUMDAR等[15]率先提出了一种基于W-M 函数的接触模型，具有不受采样长度限制且表征准确等特性。基于以上理论，陈虹旭等[16]提出了一种分段计算模型，推导出粗糙表面接触变形过程；陈建江等[17]确定了微凸体的面积分布密度函数，计算出了接触刚度和接触荷载的解析式；刘宇等[18]通过有限元软件建立三维粗糙表面模型，并研究其摩擦生热过程；冯兰兰[19]利用W-M 分形模拟了线接触粗糙表面并研究其接触特性；黄华等[20]借助W-M 分形函数，研究了新的方法，求取分形路面不平度的分形维数。本文作者从研究摊铺层表面不平顺度限值的角度出发，通过有限元软件建立摊铺层粗糙表面实体部件，结合部件与传统模型，计算不同摊铺层粗糙度作用下模型的响应，分析相关计算结果，提出摊铺层表面粗糙度的限值，以期为施工以及养护维修提供参考。

1 新型无砟轨道结构体系介绍

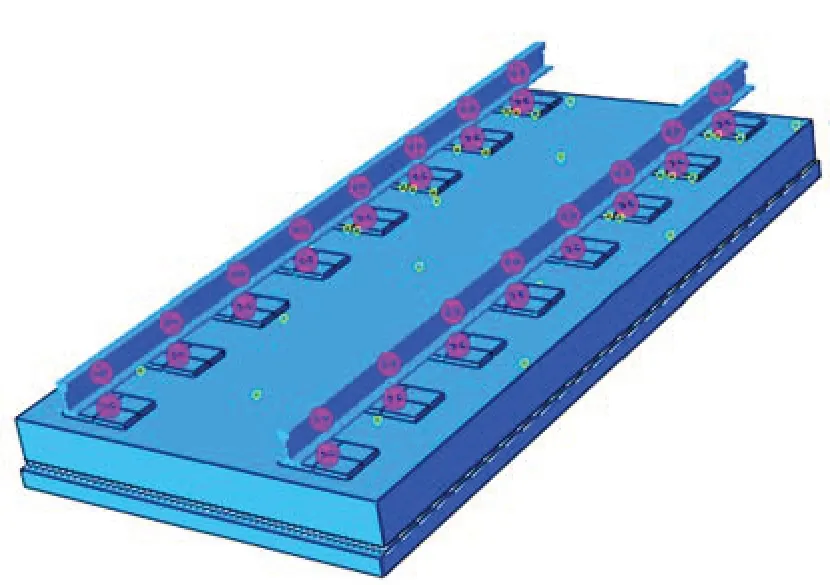
针对现有的轨道结构体系施工速度较慢，养护维修不便捷等缺点，提出了城市轨道交通新型无砟轨道结构体系。新型无砟轨道结构体系如图1所示。由图1可见：除钢轨和扣件外，新型无砟轨道结构体系由轨道板、减振垫层和混凝土摊铺层等部件组成。其中轨道板以及减振垫层由厂家预制，制作环境较理想，表面粗糙度较小，不需要考虑其表面粗糙度的问题。而混凝土摊铺层是采用大型摊铺设备将触变式混凝土材料直接摊铺形成的。一方面，这种施工方法引入大型摊铺机节省了施工时间，同时，采用触变式混凝土材料也极大地缩短了混凝土初凝时间；另一方面，这种工艺形成的混凝土摊铺层表面较为粗糙，其原因在于触变式混凝土材料本身流动性能较差以及施工过程中缺少振捣。因此，需要评价摊铺层表面的粗糙情况对轨道结构的影响，并得出相应限值以指导施工及后期养护维修。

图1 新型轨道结构示意图Fig.1 Structural diagram of new track

2 基于W-M函数的粗糙表面构造

W-M 函数[15]是模拟和重构分形表面较为通用的一种手段，较好地还原了分形表面处连续但不光滑的几何性质，其重构的表面较好地保留了原有表面的自相似性和随机性，是一种重构分形表面的典型函数。二维的W-M函数的数学表达式为

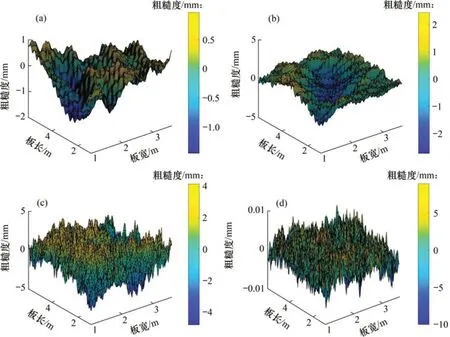
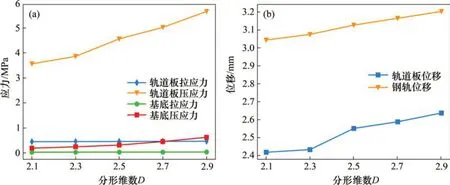
式中：Z为粗糙表面的垂直坐标；x为粗糙表面的水平坐标；D为粗糙表面的分形维数，对于二维W-M函数，1

三维W-M函数是在二维W-M函数的基础上发展得来

式中：T为随机部数；An与Bn为独立同分布的随机变量，共同服从[0，2π]的均匀分布；y为垂直于x的水平坐标，2

以W-M 分形函数为理论基础，通过Python 编程模拟出基于W-M 分形函数的粗糙表面。在本文中，模拟一块轨道板(长为4.8 m，宽为2.4 m)的粗糙表面，参考文献[17]关于采样频率的取值，在轨道板长度和宽度方向采样间隔均为0.04 m。如图2所示，直接生成的粗糙表面特征过少，并不能直接用于有限元建模。对W-M 函数进行三次样条插值处理，样条插值后的粗糙表面不仅较好地保留了原有粗糙表面的几何性质，而且能满足有限元建模的相关要求，故在后续建模中均采用三次样条插值后的数据。

为直观地反映分形维数对三维表面粗糙度的影响，尺寸常数G取固定值0.001 m，分形维数D分别取2.1，2.4，2.7和2.9，基于W-M分形函数以及三次样条插值方法，生成不同分形维度的三维粗糙表面，如图3所示。

图2 样条插值前后分形粗糙表面对比Fig.2 Comparison of fractal surfaces before and after cubic spline interpolation

图3 基于不同分形维数D的分形粗糙表面Fig.3 Fractal rough surface based on different fractal dimensions

由图3可见：基于W-M 分形函数构造的三维粗糙表面具有明显的不规则性和较好的随机性。当分形维数D取2.1时，三维粗糙表面各部分起伏较为平缓，表面褶皱较少，表面结构复杂度较低。在分形维数D不断增大的过程中，三维分形表面各部分的起伏变得剧烈，表面褶皱增加，表面结构趋于复杂。由此判定，分形维数D是影响三维粗糙表面的表面粗糙程度的主要参数，通过增大分形维数D，可以有效地增大三维粗糙表面的表面粗糙程度。

3 无砟轨道系统有限元模型的建立

3.1 三维粗糙表面模型的建立

针对W-M 函数模拟生成具有随机性和自相似性的数据，采用三次样条插值处理后满足有限元建模的相关要求，但是编程软件并没有直接输出ABAQUS 标准输入文件的方法，故需要编写相关程序将数据输出成STL 文件。将STL 文件导入Geomagic DX软件，通过面片修补，精确曲面生成等命令生成三维实体模型。取尺寸常数G为0.01 m，分形维度D为2.7，生成的三维粗糙表面模型如图4所示。

图4 三维粗糙表面模型Fig.4 3D rough surface model

由图4可见：生成的三维粗糙表面具有较高的随机性和自相似性，既满足分形表面的相关性质，又满足模拟混凝土粗糙表面的现实需求，采用该方法生成的三维粗糙表面模型能够满足下一步有限元建模的要求。通过采用不同的尺寸常数G和分形维度D的组合，生成任意三维粗糙表面模型。

3.2 无砟轨道系统有限元模型的建立

无砟轨道系统由钢轨、扣件系统、轨道板、弹性垫层以及混凝土摊铺层组成，具体模型如图5所示。为了减少计算量，钢轨采用Euler 梁单元模拟，使用Euler 梁单元既能简化计算过程，又能保证足够的数值精度[7]。扣件系统采用弹簧阻尼单元进行模拟。轨道板、弹性垫层以及混凝土摊铺层均采用实体单元进行建模。

图5 无砟轨道系统有限元模型Fig.5 Finite element model of ballastless track system

有限元模型约束为轨道板两端设置纵向以及横向约束，钢轨两端完全固定，混凝土摊铺层底面完全固定。轨道板与弹性垫层，弹性垫层与混凝土摊铺层之间的垂向接触类型均为“硬接触”，切向接触类型均为“罚接触”，摩擦因数取0.7。各部件具体的材料参数如表1所示。考虑到混凝土摊铺层表面存在大量几何不平顺，故采用显式动力学分析，荷载取轴质量16 t，工况为准静态分析，荷载因子取1.5，荷载作用位置为轨道板中部。在实验板两端另外放置基底光滑的普通板，以减小边界效应的影响。

4 有限元仿真结果分析

4.1 有限元模型验证

为验证模型的可靠性，将混凝土摊铺层设置成理想的光滑平面。将计算结果与文献[21-22]进行对比。由于文献[21-22]均没有计算弹性垫层面刚度为0.14 N/mm3的工况，故采用插值等方法合理估计该刚度的轨道结构位移。具体计算结果如表2所示。

表1 各部件材料参数Table 1 Material parameters of each component

表2 本文计算结果与相关文献对比Table 2 Comparison of calculation results between this paper and related literature mm

由表2可知，本文计算结果与文献计算结果较为接近，分析误差产生的原因是垫层厚度取值以及支撑方式等方面的差异。综上，本文计算结果与文献计算结果较为接近，具有一定程度的可信度，可以用作下一步计算分析。

4.2 不设置弹性垫层的仿真结果

在原模型的基础上取消减振垫层，并且通过不断调整特征常数G和分形维数D，改变轨道结构摊铺层的粗糙度，直到轨道系统响应超过限值，图6所示为不同粗糙度情况下轨道板的位移响应以及应力响应。由图6可见：随着粗糙度增加，轨道板应力分布表现出更强的随机性，局部地区出现应力集中现象。

图6 不同粗糙度情况下轨道板响应云图Fig.6 Response cloud map of track slab under different roughnesses

轨道结构各部件力学响应如表3所示。由表3可知，摊铺层完全光滑时，轨道结构各部分响应均未超过相关轨道结构安全性以及耐久性的限值，能够满足轨道结构的服役要求；改变基底粗糙度，取G=1 mm，D=2.1，轨道板最大拉应力为4.15 MPa，轨道板最大拉应力已经超过C40抗拉极限强度，无垫层的轨道结构会因拉应力过大而开裂，不能满足服役要求。

实施现场浇筑或摊铺工序的实际工程中，很难将混凝土粗糙度控制在1 mm以内。在相同条件下，采用弹性垫层的轨道结构，轨道板最大拉应力仅为0.447 MPa。其余各部分力学响应均满足要求。

表3 不设置弹性垫层的轨道力学响应Table 3 Mechanical response of track structure without elastic cushion

综上所述，为满足安全性和耐久性方面的需求，轨道结构需要铺设弹性垫层。

4.3 不同粗糙度下各部件响应结果

通过不断调整特征常数G和分形维数D，改变摊铺层的粗糙度，并将改变粗糙度之后的粗糙垫层作为部件导入原有模型参加计算，直到新型轨道结构系统的某部分力学响应超过相关限值的要求。相关限值主要参考文献[4-5]。

本文采用网格搜索法确定基底粗糙度的限值。设置分形维数D的取值空间为2.1，2.3，2.5，2.7和2.9。特征常数G的取值空间为从0.001 m 开始，依次递增，直到有限元计算结果中轨道结构某部分响应的相关指标超限。

为防止多变量对仿真结果的干扰，采用控制变量法，固定特征常数G的取值为0.001 m，分别计算不同分形维度D下的轨道结构响应。

不同分形维度下轨道结构各部分响应如图7所示，由图7可见：当特征常数G固定时，轨道结构各部分的响应均呈现严格的单调递增趋势，且随着分形维数D增加，轨道结构各部分响应增加趋势加剧。

不同粗糙度的轨道结构的层间接触会发生变化，层间接触变化主要体现为接触面积的变化。当摊铺层粗糙度增加时，层间接触面积减小，具体接触面积见表4。

由图7可知，当分形维数D在2.1到2.9之间取值时，轨道结构各部分响应均呈现递增趋势。为了简化计算流程，节约计算时间，在之后分析过程中分形维数D只计算2.1以及2.9这2种工况。

轨道结构各部件的响应如表4所示，分形维数D取值为2.1 和2.9，特征常数G从初始值0.001 m开始递增，递增幅度为0.001 m。当特征常数G从0.001 m增加到0.004 m时，轨道结构的应力响应以及位移响应均不断增大。当特征常数G取0.004 m，分形维度D取2.1时，轨道板位移超过文献[5]中轨道板位移不能大于3 mm的规定。

综上所述，摊铺层粗糙度应当控制在G=0.004 m，D=2.1 之下。根据计算结果：特征常数G的取值控制在0.003 m以下时，分形维数D取任意值，轨道结构响应均满足要求。同时考虑现场实测的困难性，依旧采用传统的粗糙度测量概念，即粗糙度测量曲线幅值不应大于3 mm。

图7 不同分形维度下轨道结构各部件的响应Fig.7 Response of different parts of track structure under different fractal dimensions

表4 不同粗糙度下轨道结构各部件响应Table 4 Response of different parts of track structure under different roughness

5 结论

1)分形维数D是影响三维粗糙表面的表面粗糙程度的主要参数，分形维数越大，三维表面越粗糙。

2)无弹性垫层的轨道结构不能满足服役要求。

3)当特征常数G不变时，随着分形维数D增加，轨道结构各部分的响应均增大，两者呈明显正相关关系。

4)有限元仿真计算结果表明，当特征常数G=0.004 m，D=2.1 时，轨道板位移超过相关规范限值；当G≤0.003 m时，分形维数D取任意值，轨道结构响应均满足要求。

5)综合考虑系统服役的安全性和现场测量操作的可行性，建议城市轨道交通板式无砟轨道结构摊铺层表面的粗糙度测量曲线幅值不应大于3 mm。