考虑桩周土竖向作用和施工扰动效应时大直径楔形桩的纵向振动特性

高 柳， 王奎华， 李振亚， 郭海超, 王 宁

(1.浙江大学 滨海和城市岩土工程研究中心，杭州 310058; 2.浙江大学 软弱土与环境土工教育部重点实验室，杭州 310058； 3.华东交通大学 土木建筑学院， 南昌 330000)

近年来，楔形桩由于其良好的承载性能受到了广泛的关注。楔形桩倾斜的侧面能够充分地与桩周土相互作用，在楔形侧面除了切向力外，桩周土对楔形侧面还产生一法向力。为了研究楔形桩的承载特性，国内外众多学者分别采用现场和模型试验[1-3]、理论方法[4-5]以及数值模拟[6-7]对其进行研究。试验资料表明，在相同的土质条件下，楔形摩擦桩与均匀截面摩擦桩相比，单位体积承载力高0.5倍～2.5倍，基础工程造价降低40%～60%。由此可见，楔形桩可用于桥梁地基以及处理软弱地基等等。但是，楔形桩目前在我国并没有得到广泛的应用，一方面是由于施工工艺相对传统的均匀截面桩较为复杂，另一方面就是有关楔形桩桩身侧面与桩周土的相互作用机理的了解还不够充分。对此，蔡燕燕等[8]通过将桩土系统划分为相当数量的薄层，利用平面应变模型得出了楔形桩桩顶的纵向振动阻抗的解析解。吴文兵等[9]在此基础上考虑了楔形桩的横向惯性效应，得出了考虑横向惯性效应的楔形桩纵向振动阻抗。吴文兵等[10]基于复刚度传递多圈层平面应变模型研究了考虑挤土效应时楔形桩纵向振动阻抗。Wu等[11]研究了考虑挤土效应时楔形桩扭转振动阻抗。在将桩身划分为微元段来求解桩顶阻抗时，由于相邻微元桩段半径的不同，相邻微元桩段交界面处会形成一个与土相互作用的环形截面，周燕燕等的研究都只考虑了桩周土与微元桩段侧面的竖向剪切作用而忽略了桩周土对相邻微元桩段交界面处环形截面的法向作用，本文称之为桩周土的竖向作用。

另一方面，桩基特别是大直径桩的施工会对桩周土造成相当程度的扰动。施工扰动会使桩周土在一定范围内压实或者软化。无论是桩周土的压实或者软化，本质上讲都是施工扰动造成了桩周土径向的非均质性。徐建平等[12]利用模型试验得到了沉桩过程中土体位移随水平和深度方向的变化规律,龚晓南等[13]对静力压桩所涉及的几个力学问题进行分析，提出了进一步研究这一问题的合理方法。王奎华等[14]基于复刚度传递多圈层平面应变模型研究了桩周土径向非均质性对桩顶阻抗的影响。谢帮华等研究了考虑挤土效应时楔形桩纵向振动阻抗，但只考虑了施工扰动造成桩周土压实的情况。在实际工程中，施工扰动造成桩周土软化的情况也是很常见的，特别是对于结构性比较强的软黏土而言，因此研究这一情况下楔形桩的动力特性也是很有必要的。

基于以上问题，本文研究了考虑桩周土竖向作用和施工扰动效应时大直径楔形桩的纵向振动特性，在前人的研究基础上进一步验证了楔形桩承载性能的优越性，为进一步推广楔形桩的工程使用奠定了理论基础。

1 定解问题

1.1 计算模型

本文研究分层土中考虑桩周土竖向作用和施工扰动效应时楔形桩的纵向振动特性。图1(a)表示桩土系统简图。图1(b)表示根据楔形桩桩身变截面的性质和桩周土的分层情况，将桩土系统由桩底到桩顶划分为数量足够多的n微元层，层数由下往上分别标为1, …,k, …,n，并认为在每一微元层里微元桩段近似看为圆柱体。ρpk、Vpk、Apk分别为第k微元桩段的密度、弹性波速、横截面积。H、rb、θ分别表示楔形桩的桩长、桩底半径、桩身楔角，则第k微元桩段的半径为rk=rb+(k-1)(H/n)tanθ。第k微元桩段与第k-1微元桩段的交界面上的环形截面与桩周土的相互作用可以用Voigt体来模拟，其弹簧和粘壶系数分别表示为kk-1, k和ck-1, k。桩底与桩底土的作用可以用Voigt体模拟，其弹簧系数kb和粘壶系数cb的取值可根据Lysmer等[15]根据弹性半空间理论推导出的公式计算：

(1a)

(1b)

式中：Gb为桩底土剪切模量；vb为桩底土泊松比；ρb为桩底土密度；r1为第一微元桩段的半径。

(a)桩土系统简图

(b)简化计算模型图1 桩土系统简图及简化计算模型Fig.1 Geometric model

1.2 桩周土的施工扰动效应

图2 多圈层模型示意图Fig.2 Model of composite layer

1.3 桩周土的竖向作用

图3反映相邻微元桩段及其与桩周土的相互作用关系。假想第k微元桩段桩底整个(即图3(b)中半径为rk的圆形)置于第k-1微元土层上，那么第k微元桩段桩底与第k-1微元土层的相互作用就类似于桩底与桩底土的相互作用，因此可以用Voigt体模拟，其弹簧和粘壶系数为kk和ck。同理，图3(b)中半径为rk-1的圆形与第k-1微元土层的相互作用也可以用Voigt体模拟，并且其弹簧和粘壶系数为kk-1和ck-1。Pkb(t)表示第k微元桩段桩底的轴力；Pk-1, k(t)表示第k-1微元桩段桩顶的轴力；Pk-1, k(t)表示第k-1微元土层对图3(b)中环形截面的法向作用力；fk(z,t)表示第k微元土层对桩身的侧摩阻力。

根据式(1a)和式(1b)。可以求得kk、ck、kk-1、ck-1：

(2a)

(2b)

图3 相邻两段的相互作用关系Fig.3 Idealization of two typical adjacent segments

(2c)

(2d)

式中：ρs(k-1)和vs(k-1)分别表示第k-1微元土层的密度和泊松比；Gk-1, 1为第k-1微元土层扰动区第一圈层土体的剪切模量。

当图3(b)所示截面发生位移uk-1, k时，第k-1微元土层对图3(b)中半径为rk、rk-1的圆形截面的法向作用力Pk(t)、Pk-1(t)分别为

(3a)

(3b)

那么，第k-1微元土层对图3(b)中环形截面的法向作用力Pk-1, k(t)为

(4a)

则有：

(4b)

(4c)

写成这种形式是为了方便后续的编程计算。

1.4 假设条件

(1) 楔形桩为大直径、黏弹性、圆形均匀变截面桩，桩身截面半径随着深度增加而均匀变小。

(2) 桩周土采用平面应变模型，桩周土层沿径向无限延伸，土体表面为自由界面；由施工扰动效应引起的桩周土性质的变化是连续的。

(3) 桩底与土的相互作用采用Voigt体模拟；桩土简化计算模型中第k微元桩段与第k-1微元桩段交界面上的环形截面与桩周土的相互作用采用Voigt体模拟。

(4) 楔形桩与桩周土交界面上位移和应力连续。

2 桩土动力平衡方程的求解

2.1 微元土体动力平衡方程及求解

Novak[16]给出了平面应变模型的土体动力平衡方程，第k微元土层中第j圈层的土体动力平衡方程为：

(5)

式中：Wk, j表示第k微元土层中第j圈层的土体纵向振动位移。

式(5)的解可表示为

Wk, j=Ak, jK0(βk, jr)+Bk, jI0(βk, jr)

(6)

土体中的剪应力为

(7)

式中：I1(βk, jr)、K1(βk, jr)分别为一阶的第一类和第二类修正Bessel函数。

(1) 未扰动区

取j=m+1，则式(5)～(7)适用于未扰动区土体。由于无穷远处土体位移衰减为零，结合贝塞尔函数的性质，可得Bk, m+1=0。根据剪切刚度的定义，未扰动区与扰动区交界面(r=rk, m)上的剪切刚度为：

(8)

(2) 扰动区

当1≤j≤m时，则式(5)～(7)适用于扰动区土体。则第j圈层外层(r=rk, j)的剪切刚度为：

(9)

由式(9)可得到

(10)

第j圈层内层(r=rk, j-1)的剪切刚度为：

KKk, j-1=

(11)

式(9)～(11)给出了同一圈层内层和外层的剪切刚度的递推关系，结合式(8)，即可求得第k微元土层对微元桩段的剪切刚度KKk。

2.2 微元桩段动力平衡方程及求解

本文采用Rayleigh-Love杆模型来考虑微元桩段动力特性，它能够考虑微元桩段的横向惯性效应。令uk=uk(z,t)表示桩身位移，则第k微元桩段的动力平衡方程为

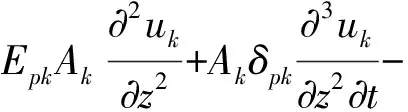
(12)

式中：Epk、Ak、ρpk、vpk、δpk分别为第k微元桩段桩身弹性模量、截面积、材料密度、泊松比、阻尼系数；fk(z,t)表示第k微元土层对桩身的侧摩阻力，且有fk(z,t)=KKkuk(z,t)。

为了方便后面的公式推导，对于每一个微元桩段，取原点位于微元桩段桩底的局部坐标系Q′z′r′，其中z′轴方向竖直向上。

桩身质点位移和速度初始条件为：

uk(z′, 0)=0

(13a)

(13b)

结合初始条件式(13a)、(13b)，对式(12)进行拉普拉斯变换,可以得到：

(14)

式(14)的解可以表示为

Uk(z′,s)=Mkcos (λkz′)+Nksin(λkz′)

(15a)

式中

(15b)

式中：Mk、Nk为由边界条件确定的常数。

由阻抗函数的定义，可求得第k微元桩段桩顶的阻抗函数Zka：

(16)

式中：φk=arctan(Nk/Mk)，可由第k微元桩段桩底的阻抗函数Zkb求得：

(17)

2.3 桩顶阻抗求解

图3(b)所示截面上的位移连续条件和应力平衡条件为

uk(z′,t)|z′=0=uk-1(z′,t)|z′=hk-1

(18)

Pkb(t)=Pk-1, k(t)+P(k-1)a(t)

(19)

式中：Pkb(t)表示第k微元桩段桩底的轴力；P(k-1)a(t)表示第k-1微元桩段桩顶的轴力。

对上述两式进行拉普拉斯变换，用(19)两端除以式(18)两端，结合式(4a)和阻抗函数的定义，可以得到

Zkb(s)=Z(k-1)a(s)+kk-1, k+s·ck-1, k

(20)

式中：kk-1, k、ck-1, k由式(4b)、(4c)给出。Zkb(s)表示第k微元桩段桩底的阻抗函数，Z(k-1)a(s)表示第k-1微元桩段桩顶的阻抗函数。

在蔡燕燕等的研究中，在求解楔形桩桩顶的阻抗函数时，令相邻微元桩段的交界面上阻抗函数相等，这也是现今广泛使用的阻抗函数递推法。传统的阻抗函数递推法忽略了相邻微元桩段交界面上环形截面与土的相互作用，式(20)给出了考虑其作用的相邻微元桩段的交界面上阻抗函数递推关系，本文称之为修正的阻抗函数递推法。

楔形桩桩底的边界条件为

(21)

对式(21)进行拉普拉斯变换，结合阻抗函数的定义，可得楔形桩桩底的阻抗函数：

Z1b(s)=kb+s·cb

(22)

式(16)、(17)确定了微元桩段的桩顶与桩底的阻抗函数之间的关系；式(20)给出了相邻桩段在交界面上的阻抗函数递推关系；式(22)给出了桩底阻抗函数。结合式(16)、(17)、(20)、(22)，就可求得桩顶阻抗函数Zna(s)：

Zna=Kna+iCna

(23)

阻抗函数的实部Kna表示桩顶真实的动刚度，反映了桩顶抵抗纵向变形的能力，虚部Cna代表桩顶的动阻尼，反映了桩身内应力波的能量耗散特性。

3 扰动区划分层数的影响

如果没有特别说明，本文的桩土系统计算参数取如下值：桩周土密度ρs=2 000 kg/m3，扰动区圈层厚度d=rb，材料阻尼系数Ds=0.001，外部未扰动区土体剪切波速Vs=160 m/s；桩底土剪切波速Vb=160 m/s，密度ρb=2 000 kg/m3；桩身材料密度ρp=2 500 kg/m3，阻尼系数δp=0.001，桩底半径rb=0.6 m，桩身楔角θ=2°。

蔡燕燕、吴文兵等研究了桩土系统划分层数对桩顶动阻抗的影响：当n≥100时，桩顶阻抗几乎不再发生变化，也就是说满足计算精度要求。本文中n取200。上述研究是基于桩周土压实的情况。在实际工程中，由于施工工艺和桩周土性质的影响，施工扰动也会造成桩周土的软化，因此有必要研究桩周土扰动区软化情况下桩周土扰动区划分层数对桩顶动阻抗的影响。

由图4(a)可以看出，对于同一频率，随着扰动区划分层数m的增大，桩顶的动刚度变大，且随着频率的增大，增大的幅度变大。当m≥30时，动刚度曲线几乎不再变化，此时m已经满足动刚度计算精度要求。由图4(b)可以看出，对于同一频率，随着扰动区划分层数m的增大，桩顶的动阻尼也随之变大，且随着频率的增大，动阻尼增大的幅度变大。当m>20后，动阻尼曲线几乎不变化，此时已经满足动阻尼计算精度要求。综上所述，m≥30时满足桩顶阻抗的精度计算要求，本文中m取40。

(a) 动刚度

(b) 动阻尼图4 扰动区划分层数对桩顶阻抗的影响Fig.4 Effect of slice of disturbed section on impedance function at pile top

4 与已有解的对比

为了研究楔形桩的桩顶阻抗特性，蔡燕燕等提出了既不考虑桩身横向惯性效应也不考虑施工扰动效应的解，吴文兵等提出了考虑桩身横向惯性效应但不考虑施工扰动效应的解，谢帮华等提出了考虑桩周土挤土效应的解。但是上述解都没考虑桩周土的竖向作用。将本文解中的kk-1, k和ck-1, k取为零，即退化到谢帮华等所得解，再将桩周土扰动范围d取为零，则退化到吴文兵等所得解，进一步将桩身泊松比vp取为零，则退化到蔡燕燕等所得解，这也验证了本文所得解的合理性。

图5反映了在桩基础动力设计所关注的低频范围内，本文解与蔡燕燕、吴文兵以及谢帮华等所提出的解的对比。由于谢帮华等研究的是考虑施工扰动使得桩周土压实的桩顶动力特性，本节为了与其保持一致，外部未扰动区到内部扰动区土体剪切波速Vs由150 m/s线性增加到250 m/s。由图5(a)可以看出，吴文兵与蔡燕燕的解是等价的，也就是说，泊松比对桩顶动刚度没有影响。谢帮华的解表明，在考虑了施工扰动效应对桩周土的压实作用后，在较低频率范围内，动刚度随着频率的增加而逐渐增加，频率超过一定范围后再逐渐减小。谢帮华的解与吴文兵的解存在一个交界点，在这个交界点之前，施工扰动效应的压实作用使得桩顶动刚度有所增加，在交界点之后，施工扰动效应的压实作用使得桩顶动刚度明显降低。本文的解表明，在考虑了桩周土的竖向作用后，桩顶动刚度变化趋势基本不变，但是幅值有明显的增加，而且上述交界点明显向右移动，也就是说，桩周土竖向作用显著增加了桩顶抵抗变形的能力。由图5(b)可以看出，吴文兵与蔡燕燕的解是等价的，桩身泊松比对桩顶动阻尼的影响可以忽略。施工扰动效应的压实作用使得桩顶动阻尼有明显的增加，增加的幅值随着频率的增加而线性增大。桩周土的竖向作用进一步增大了桩顶动阻尼，但增大的幅值相对较弱。

(a) 动刚度

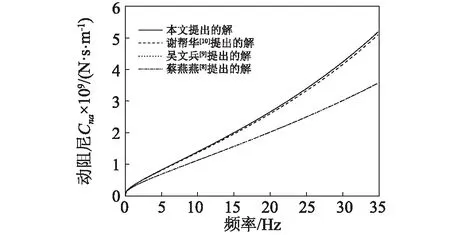
(b) 动阻尼图5 本文解与前人解的比较Fig.5 Comparison with other solutions

5 参数分析

施工扰动效应会造成桩周土的压实或软化，本节研究这两种情况下桩周土竖向作用与施工扰动效应的耦合作用。

5.1 压实程度

本节用q(桩周扰动区内侧土体与未扰动区土体的剪切波速比)表示桩周土的压实程度。外部未扰动区土体剪切波速取160 m/s。剪切波速比q=1.2，1.6，2.0，2.4。其余桩土参数如第3节所述。为了图形表述简洁，当kk-1, k≠0时，代表此时ck-1, k≠0，所得解考虑了桩周土的竖向作用；当kk-1, k=0时，代表此时ck-1, k=0，所得解忽略了桩周土的竖向作用。由图6(a)可以看到，当不考虑桩周土竖向作用时，对于同一频率，在0～8 Hz的较低频率范围内，桩顶动刚度随着桩周土压实程度的增加而略微增大，当频率大于8 Hz时，随着压实程度的增加，桩顶动刚度明显减小。考虑了桩周土的竖向作用后，桩顶动刚度有明显的增大，且压实程度越大，桩顶动刚度增大的幅度越大。由于桩周土的竖向作用，桩顶动刚度曲线呈现了新的规律：在0～26 Hz的频率范围内，随着压实程度的增加，桩顶动刚度有明显的增大，当频率大于26 Hz时，桩顶动刚度随着压实程度的增大而减小。上述分析表明，桩周土的竖向作用明显增加了楔形桩抵抗纵向变形的能力。图6(b)表明，对于同一频率而言，随着压实程度的增大，桩顶动阻尼增大，由于桩周土竖向作用所引起的桩顶动阻尼的增大却变小，当q=2.4时，桩周土竖向作用对桩顶动阻尼几乎没有影响。

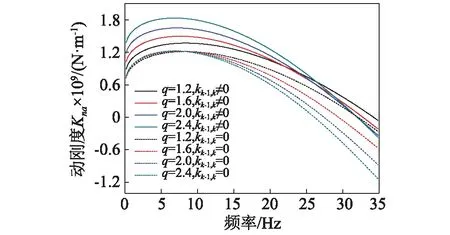
(a) 动刚度

(b) 动阻尼图6 不同压实程度下桩周土竖向作用对桩顶阻抗的影响Fig.6 Effect of vertical reaction of surrounding soil on impedance function at pile top when compact degree varies

5.2 压实范围

为了在桩基动力设计所关心的低频范围内研究施工扰动效应造成的桩周土压实范围d的影响，分别取d=0.5rb, 1rb, 1.5rb, 2rb，剪切波速比q=1.5。

由图7(a)可以看出，随着压实范围的增大，由于桩周土竖向作用引起的桩顶动刚度的增大的幅度并没有明显的变化，故桩顶动刚度随着压实范围增大而变化的规律保持不变：在频率为0～13 Hz范围内，对于同一频率，桩顶动刚度随着压实范围的增大而增大，但幅度很小；当频率大于13 Hz时，对于同一频率，随着压实范围的增大，桩顶动刚度先减小，然后快速增大。由图7(b)可以看出，对于同一频率，随着压实范围的增大，桩顶动阻尼明显增大，由于桩周土竖向作用所引起的桩顶动阻尼的增大幅值则明显降低。

(a) 动刚度

(b) 动阻尼图7 不同压实范围下桩周土竖向作用对桩顶阻抗的影响Fig.7 Effect of vertical reaction of surrounding soil on impedance function at pile top when compact range varies

5.3 软化程度

当q<1时，表示施工扰动效应造成了桩周土的软化。本节为了研究桩周土软化程度与桩周土竖向作用的耦合作用，分别取q=1，0.8，0.6，0.4，软化范围d=rb。

图8反映了桩周土不同软化程度下桩周土竖向作用对桩顶阻抗的影响。由图8(a)可以看到，随着桩周土软化程度的增大(q值减小)，由于桩周土竖向作用引起的桩顶动刚度的增大迅速减小。在考虑了桩周土的竖向作用后，当桩周土软化程度在较低范围内增大时，由于桩周土软化程度增大所引起的桩顶动刚度的减小值随着频率的增大先增大后减小；当桩周土软化程度在较高范围内增大时，由于桩周土软化程度增大所引起的桩顶动刚度的减小值随着频率的增大而单调增大。综上所述，当桩周土软化程度较大时，由于桩周土竖向作用所引起的桩顶动刚度的增大很微弱，由于桩周土软化所引起的动刚度的减小却很明显。由图8(b)可知，对于同一频率，随着桩周土软化程度的增大，桩顶动阻尼的减小很明显，由于桩周土竖向作用所引起的桩顶动阻尼的增加则略微减小。

(a) 动刚度

(b) 动阻尼图8 不同软化程度下桩周土竖向作用对桩顶阻抗的影响Fig.8 Effect of vertical reaction of surrounding soil on impedance function at pile top when soften degree varies

5.4 软化范围

为了在桩基动力设计所关心的低频范围内研究桩周土软化范围d对桩顶动刚度的影响，分别取d=0.5rb,1rb,1.5rb,2rb，剪切波速比q=0.6。

图9反映了不同桩周土软化范围下桩周土竖向作用对桩顶阻抗的影响。由图9(a)可以看出，在施工扰动造成桩周土软化的情况下，对于同一频率，随着扰动范围的增大，桩顶动刚度减小，并且减小的幅值随着频率的增加而变大，由于桩周土竖向作用所引起的桩顶动刚度的增加基本上保持不变。值得注意的是，不同软化范围下的桩顶动刚度曲线起始点大致相同，也就是说，在相同静荷载作用下，桩周土软化程度相同而软化范围不同时，桩顶沉降相同。从图9(b)可以看出，随着软化范围的增加，对于同一频率，桩顶动阻尼降低，由桩周土竖向作用引起的桩顶动阻尼的增大保持不变。当d=2rb，频率达到25 Hz时，桩顶动阻尼增大的速率会急剧变大，进一步的研究表明，扰动范围较小时也存在着这种变化规律，只是此时转折点大于35 Hz而没有被反映在图中。

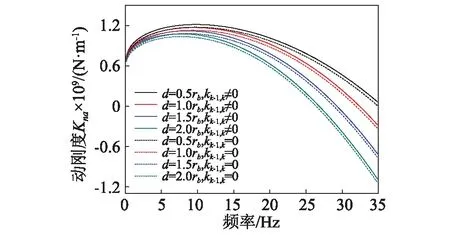
(a) 动刚度

(b) 动阻尼图9 不同软化范围下桩周土竖向作用对桩顶阻抗的影响Fig.9 Effect of vertical reaction of surrounding soil on impedance function at pile top when soften range varies

6 结 论

将桩土系统划分为数量足够多的微元层，基于复刚度传递多圈层法，求出桩侧土对桩身的剪切刚度。通过本文推导出的修正的阻抗函数递推法求得大直径楔形桩桩顶的阻抗函数。

(1)将本文解与已有解进行比较。在施工扰动效应造成桩周土压实的情况下，考虑了桩周土的竖向作用后，桩顶动刚度变化趋势基本不变，但是幅值有明显的增加，桩顶动阻尼有微弱的增加，且增加的幅值随着频率的增加而变大。通过与已有解的对比进一步验证了楔形桩承载性能的优越性。

(2)研究了在施工扰动效应造成桩周土压实和软化这两种情况下，桩周土竖向作用与施工扰动效应的耦合作用。随着压实程度的增大，由于桩周土竖向作引起桩顶动刚度的增大有明显的增大，桩顶动阻尼的增大则明显变小；随着压实范围的增大，由于桩周土竖向作用引起的桩顶动刚度的增大幅度并没有明显的变化，由于桩周土竖向作用所引起的桩顶动阻尼的增大幅值则明显降低；随着桩周土软化程度的增大，由于桩周土竖向作用引起的桩顶动刚度的增大迅速减小，桩顶动阻尼的增加则略微减小；随着软化范围的增大，由于桩周土竖向作用所引起的桩顶动刚度的增加基本不变，桩顶动阻尼的增大也几乎不变。

[ 1 ] WEI J Q, HESHAM M. Experimental study of axial behaviour of tapered piles[J]. Canadian Geotechnical Journal, 1998, 35(4): 641-654.

[ 2 ] EI NAGGAR M H, MOHAMMED S. Evaluation of axial performance of tapered piles from centifuge tests[J]. Canadian Geotechnical Journal, 2000, 37(6): 1295-1308.

[ 3 ] MOHAMMED S, EI NAGGAR M H, MONCEF N. Load transfer of fiber-reinforced polymer(FRP) composite tapered piles in dense sand[J]. Canadian Geotechnical Journal, 2004, 41(1): 70-95.

[ 4 ] KODIKARA J K, MOORE I D. Axial response tapered piles in cohesive frictional ground[J]. Journal of Geotechnical and Geoenvironmental Enginnering, 1993, 1991(4): 675-693.

[ 5 ] EI NAGGAR M H, WEI J Q. Uplift behavior of tapered piles established from model tests[J]. Canadian Geotechnical Journal, 2000, 31(7): 56-74.

[ 6 ] TAKE W A, WALSANGKAR A J. The elastic analysis of compressible tin-piles and pile groups[J]. Geotechnique, 2002, 31(4): 456-474.

[ 7 ] MOHAMEDZEIN Y E, MOHAMED M G. Finite analysis of axially tin-pile groups[J]. Computers and Geotechnics, 2001, 26(2): 231-243.

[ 8 ] 蔡燕燕，俞缙，郑春婷，等. 楔形桩桩顶振动阻抗的解析解[J]. 岩土工程学报，2011,33(增刊2): 392-398.

CAI Yanyan, YU Jin, ZHENG Chunting, et al. Analytical solution for longitudinal dynamic complex impedance of tapered pile[J]. Chinese Journal of Geotechical Engineering, 2011, 33(Sup2): 392-398.

[ 9 ] 吴文兵，王奎华，武登辉，等. 考虑横向惯性效应时楔形桩纵向振动阻抗研究[J]. 岩土力学与工程学报，2011,30(增刊2)：3618-3625.

WU Wenbing, WANG Kuihua, WU Denghui, et al. Study of dynamic longitudinal impedance of tapered pile considering lateral inertial effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Sup2): 3618-3625.

[10] 吴文兵，谢帮华，黄生根， 等. 考虑挤土效应时楔形桩纵向振动阻抗研究[J]. 地震工程学报， 2015, 37(4): 1042-1047.

WU Wenbing, XIE Banghua, HUANG Shenggen, et al. Vertical dynamic impedance of tapered piles considering compacting effects[J]. China Earthquake Engineering Journal, 2015, 37(4): 1042-1047.

[11] WU Wenbing， JIANG Guosheng, LÜ Shuhui, et al. Torsional dynamic impedance of a tapered pile considering its construction disturbance effect[J]. Marine Georesources & Geotechnology, 2016, 34(4): 321-330.

[12] 徐建平，周健，许朝阳，等.沉桩挤土效应的模型试验研究[J]. 岩土力学，2000,21(3)：235-238.

XU Jianping, ZHOU Jian, XU Chaoyang, et al. Model test research on pile driving effect of squeezing against soil[J]. Rock and Soil Mechanics, 2000, 21(3):235-238.

[13] 龚晓南，李向红. 静力压桩挤土效应中的若干力学问题[J]. 工程力学，2000,17(4): 7-13.

GONG Xiaonan, LI Xianghong. Several mechanical problems in compacting effects of static piling in soft clay ground [J]. Engineering Mechanics, 2000, 17(4) : 7-13.

[14] 王奎华，杨冬英，张智卿.基于复刚度传递多圈层平面应变模型的桩动力响应研究[J].岩石力学与工程学报,2008,27(4):825-831.

WANG Kuihua, YANG Dongying, ZHANG Zhiqing. Study on dynamic response of pile based on complex stiffness transfer model of radial multizone plane strain[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4):825-831.

[15] LYSMER J, RICHART F E. Dynamic response of footings to vertical loading[J]. Geotechnical Special Publication, 1966, 92(118): 1091-1117.

[16] NOVAK M. Dynamic stiffness and damping of piles[J]. Canadian Geotechnical Journal, 1974, 11(4):574-598.