分岔隧道过渡段的爆破振动特性研究

凌同华， 曹 峰,2， 张 胜， 张 亮， 谷淡平

(1.长沙理工大学 土木与建筑学院，长沙 410114；2.长沙理工大学 桥梁工程高校重点实验室，长沙 410114；3.湖南城市学院 土木工程学院，湖南 益阳 413000)

随着我国西部交通建设的不断发展，穿越山岭地区的高速公路隧道逐渐增多。近年来，分岔式隧道作为一种新颖的隧道结构形式受到人们广泛的关注，如沪蓉西高速公路部分隧道在国内较早采用了这种结构，其特点是能够适应多变的地质地形条件和降低工程造价，在展线困难和桥隧过渡工程中具有较好的应用前景。但该类工程涵盖了连拱、小净距和分离式三种形式，受力结构复杂，施工难度较大。其中，分岔隧道连拱段和小净距段之间的过渡段截面突变，应力集中，其安全与否已成为衡量工程成败的关键。同时，在后行隧道的爆破开挖过程中，频繁的爆破振动对先行隧道的影响较大，极易导致隧道岩体和受力结构开裂破坏，甚至失稳。因此，在分岔隧道过渡段的施工过程中，有必要研究爆破开挖对中墙和支护结构的影响，以减少爆破振动对相邻隧道的损害。

尽管分岔式公路隧道在国内外投入并使用的项目并不多[1]，但相关学者对此也进行了研究。王者超等[2]对分岔隧道的变形进行了监测，提出了相应的施工对策；蔚立元等[3]采用数值模拟和模型试验手段探讨了分岔隧道过渡段的受力变形特征。针对隧道爆破振动规律的研究，时亚昕等[4]利用数值模拟研究了连拱隧道后开挖洞室爆破振动对中隔墙的影响；贾磊等[5]通过数值模拟探讨了新建隧道爆破振动对既有邻近隧道衬砌的影响；林从谋等[6-7]采用振动监测和数值模拟方法，分析了小净距隧道的爆破振动特性及应力波的传播规律；李新平等[8-9]对地下洞室群、地下厂房的爆破振动效应进行监测及理论研究；Langefors等[10]提出隧道偏于安全的临界振动控制标准。目前国内外学者关于分岔隧道的研究多集中于围岩的受力变形和支护方案优化，爆破振动规律的研究则多以分离式隧道、连拱隧道和小净距隧道为主，而针对分岔隧道过渡段爆破振动规律的研究很少。因此，开展分岔隧道过渡段的爆破振动特性研究显得尤为重要。

本文结合湘西六月田分岔隧道过渡段的工程特点，通过现场爆破振动测试和数值模拟手段，探讨受力结构的破坏机理，分析后行隧道爆破振动波在先行隧道保留岩体、中墙及支护结构的传播与分布规律，提出后行隧道衬砌混凝土的爆破振动控制标准，从而实现分岔隧道过渡段爆破开挖的稳定性控制。

1 工程概况

永顺至吉首高速公路六月田隧道地处永顺县芙蓉镇境内，隧道左线长1 010 m(K10+445～K11+455)，右线长1 015 m(YK10+440～YK11+455)，属长隧道。工程所在区域所处地貌属于剥蚀溶蚀低山地貌，地形起伏较大，地面高程在430.60～567.10 m之间，隧道内岩石主要为微风化灰岩。为了解决桥隧过渡方面的困难，隧道出口段设计为分岔式隧道，分岔段全长106 m，其中明洞段6 m，Ⅴ级围岩连拱段32 m，Ⅳ级围岩小净距段42 m。隧道设计为双洞单向交通隧道，连拱段左右线测设线间距3～4.78 m，Ⅳ级围岩小净距段中夹岩柱净距3～6 m。隧道出口前方为猛洞河大桥。分岔段平面布置见图1。

图1 分岔段平面布置(m)Fig.1 Horizontal layout of bifurcation segment (m)

本文研究的隧道过渡段是指Ⅴ级围岩连拱段和Ⅳ级围岩小净距段之间的过渡区域。蔚立元等将过渡段研究区域定义为分界面为中心的40 m长的区间范围内。施工过程中，连拱段采用三导洞法开挖，开挖顺序依次为中导洞、两侧导洞、先行隧道上下台阶、后行隧道上下台阶。小净距段采用上下台阶法开挖，开挖完成后应及时进行初期支护。考虑到洞口段围岩较差，初期支护后应及时施作二次衬砌。

六月田分岔隧道过渡段采用新奥法施工，隧道上台阶采用楔形掏槽的爆破方法，周边眼采用光面爆破，炮孔间距50 cm。炸药选用2#岩石乳化炸药，装药炮孔直径42 mm。

2 爆破振动监测

2.1 测试方案

已有研究结果表明，在后行隧道爆破荷载作用下，先行隧道迎爆侧的振速要大于背爆侧，上台阶的爆破振速比下台阶的振速大[11]。因此，现场的爆破振动测试以采集后行隧道上台阶迎爆侧的振速为主。结合工程实际情况，监测点沿隧道纵轴线方向以4 m为间距依次布设5个断面。监测断面沿爆破开挖面前方和开挖面后方对称布置，先行隧道每个断面各2个测点，即迎爆侧拱腰和拱脚，如图2所示。

(a) 立面图

(b) 平面图图2 振速测点布置图(m)Fig.2 Layout of measuring point for vibration velocity(m)

爆破振动监测系统由NUBOX-8016爆破振动智能监测仪、TP3V-4.5三维速度型传感器等组成。图3为现场测试时的爆破振动监测系统。

图3 爆破振动监测系统Fig.3 Test system of blasting vibration

2.2 测试结果及分析

现场共进行了3次爆破振动测试，爆破开挖面桩号分别为YK11+431，YK11+417，YK11+401。实测爆破振动波形如图4所示。爆破振动部分测试数据见表1。

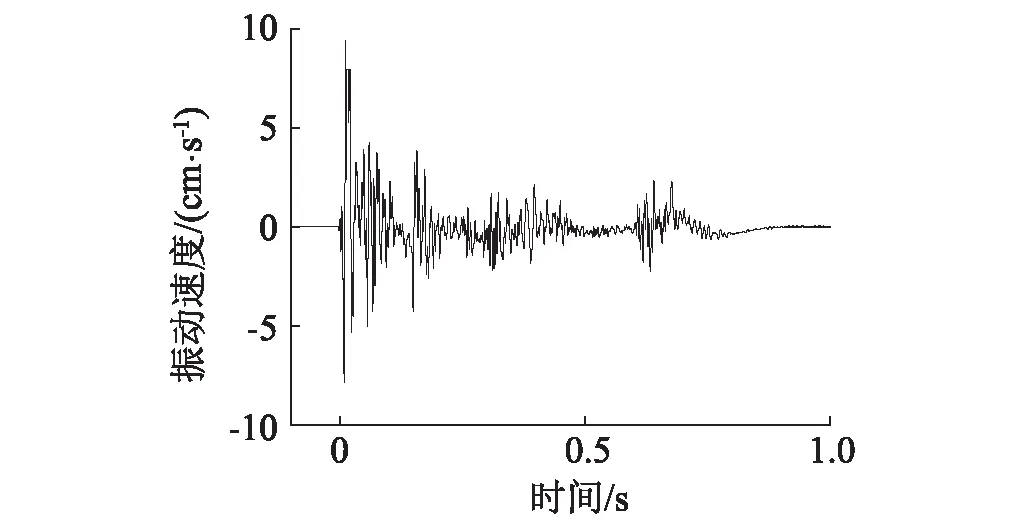
(a) 径向

(b) 切向图4 实测振速波形Fig.4 Vibration velocity waveform monitored

由图4和表1可知，掏槽孔爆破产生的振速最大。掏槽孔段装药量为6.0 kg，小于最大段药量7.2 kg或9.9 kg。由此可以看出，爆破振速与最大段药量并不成绝对正比关系。究其原因，掏槽孔爆破为单自由面条件下的岩石爆破，岩石夹制作用过大导致振速显著增加。因此，爆破开挖过程中可采用多级复式掏槽爆破，减少最大段药量，同时减弱后一级掏槽爆破时岩石的夹制作用，降低爆破振速。

表1 爆破振动部分测试数据

考虑到测点的径向和切向振速较大，选取各测点的径向和切向振速峰值，得到振速峰值特征曲线如图5所示。

(a)拱脚

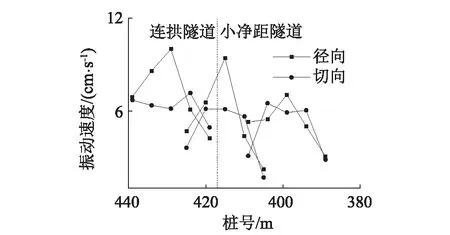
(b)拱腰图5 振速峰值特征曲线Fig.5 Characteristic curves for peak value of vibration velocity vibration velocity

由图5可见，径向振速特征曲线呈“7”字形，开挖面靠成洞区振速出现“放大”效应，而切向振速特征曲线呈山峰状，最大振速出现在距离开挖面较近的区域。从不同部位的振速来看，拱腰的最大振速大于拱脚。因此，爆破作业时，应采用迎爆侧拱腰的径向振速作为控制标准，小净距段还可将切向振速列入参考范围。

2.3 回归分析

目前主要采用萨道夫斯基经验公式对爆破振动监测数据进行回归分析，其表达式为[12]：

(1)

式中：V为质点振速(cm/s)；R为测点与爆源距离(m)；K，α分别为场地因素和衰减系数；Q为段最大装药量(kg)。

六月田隧道过渡段不同级别围岩和监测部位的振速回归经验公式见表2。由表2可以得到分岔隧道过渡段爆破地震波沿先行隧道中墙迎爆侧的传播规律。

表2 不同级别围岩和监测部位的振速回归经验公式

3 数值分析

3.1 计算模型及参数

采用LS-DYNA显式有限元程序建立三维模型，其计算尺寸为：左右X方向范围取-55～55 m，Y方向范围取上边界至地表，下边界24 m，Z方向范围(隧道纵向)取70 m。炸药、岩石、混凝土和空气均采用SOLID164单元进行模拟，模型划分网格共得131 091个实体单元。三维计算模型及网格划分见图6。

图6 计算模型及网格划分Fig.6 Computational model and meshing

根据林从谋等[14]的研究，在数值模拟中将炸药按集中装药方式进行分析，验算结果是安全的，并偏于保守。结合现场情况，连拱段上台阶炸药量取34.6 kg，小净距段上台阶炸药量取43.5 kg。数值模拟中采用集中装药方式，将相同重量的炸药模型布置在后行隧道上台阶掏槽处。

炸药的爆炸过程采用状态方程进行模拟，表现形式为[15-16]：

(2)

式中：A，B为材料常数(GPa)；R1、R2、ω为状态方程的常数；V为相对体积；E0为初始内能密度(GPa)。

采用的炸药材料及状态方程参数见表3。

表3 炸药参数

根据文献[17]对岩石的物理力学参数的描述，隧道围岩为粘土、顶板厚度小的微风化灰岩和岩质坚硬的微风化灰岩。隧道内初期支护采用C20喷射混凝土，二次衬砌采用C25混凝土。表4为围岩和混凝土的物理力学参数。

表4 围岩和混凝土的计算参数

3.2 数值模拟结果与实测结果对比分析

选取连拱段Ⅴ级围岩拱腰X方向和小净距段Ⅳ级围岩拱脚Z方向的节点振速峰值，与实测数据分别进行回归分析，见图7。经对比可知，连拱Ⅴ级围岩段拱腰径向振速的相对误差为6%，小净距Ⅳ级围岩拱脚切向振速的相对误差为4%，两者相差不大，验证了数值计算结果的准确性。

3.3 中墙振动效应分析

分岔隧道过渡段的中墙分为连拱段中隔墙和小净距段中夹岩。中墙厚度随着开挖深度的深入不断增加，而中墙的振速则随着中墙厚度的变化而不同。根据中墙的受力特点，选取的振速控制节点如图8所示。考虑到篇幅关系，本文仅列出X方向振速变化曲线如图9所示。

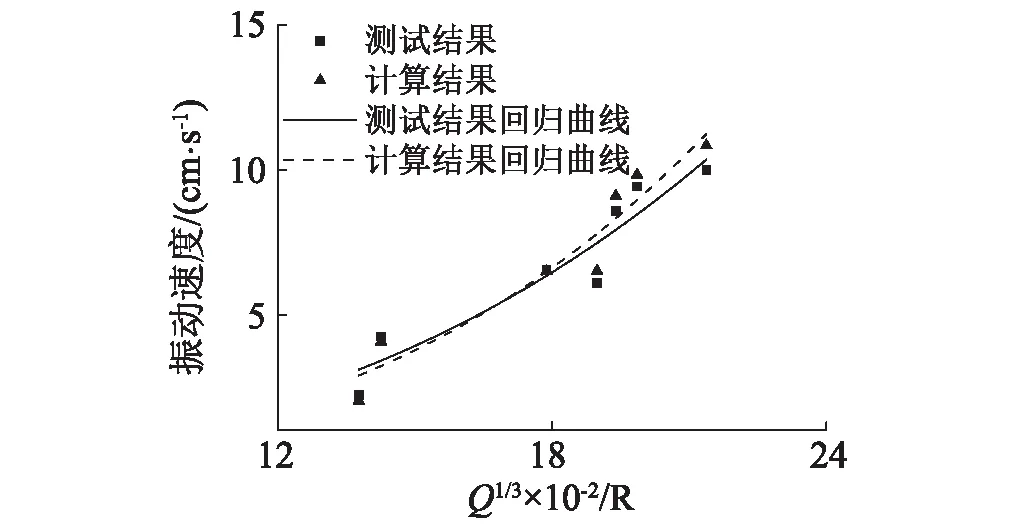
(a)连拱段Ⅴ级围岩段拱腰径向(X方向)振速

(b) 小净距段Ⅳ级围岩拱脚切向(Z方向)振速图7 现场测试与计算结果回归趋势对比Fig.7 Comparison of regression trend of vibration velocity between field test and numerical calculation

图8 中墙振速控制点布置图Fig.8 Control point arrangement of velocity of middle wall

图9 中墙控制点X方向振速曲线Fig.9 Control point curve of X direction peak particle velocity of middle wall

由图9可见，最大振速发生在3#控制点的中墙厚度1 m处，为13.74 cm/s。由于该部位临近洞口，受自由面影响，爆破地震波反射作用明显，振速显著增大。随着中墙厚度的增加，振速较大值主要发生在2#和3#控制点。

整体而言，连拱段中隔墙的振速衰减幅度更大，衰减率为小净距段中夹岩的1.43倍～6.45倍。分析原因，连拱段开挖时，受软弱围岩和中隔墙等不均匀介质的影响，爆炸应力波的传播路径发生改变，使得中隔墙处的振速峰值衰减较快。而小净距段围岩的完整性相对较好，介质较均匀，因而爆炸应力波的传播路径受到的阻隔较小，振速衰减较慢。此外，在实际的施工过程中，频繁的爆破振动对围岩造成的损伤，也是导致连拱段中隔墙爆破振速衰减较快的原因之一[18]。

3.4 横断面振动特性分析

结合分岔隧道的结构特点，选取桩号K11+431断面(1#)，K11+417断面(2#)，K11+401断面(3#)的节点振速峰值，得到X，Y，Z方向及合速度包络图如图10所示。

图10 先行隧道振速峰值全断面包络图(单位:cm/s)Fig.10 Envelope diagramof peak vibration velocity along whole cross-section of the early excavated tunnel (unit:cm/s)

可以看出，先行隧道迎爆侧拱腰的振速最大，分别为拱肩的1.02倍 ～1.14倍，拱顶的1.31倍～1.86倍，拱脚的1.27倍～1.52倍，底板的1.23倍～2.05倍。迎爆侧拱肩和拱腰的振速相差不大，均为最危险的振动破坏区。迎爆侧拱脚次之，背爆侧振速最小。从3个方向的振速来看，X方向的振速最大，Z方向次之，Y方向最小。从3个断面的振速对比可知，连拱段振速明显大于小净距段，但迎爆侧拱腰的振速相差不大。究其原因，连拱段迎爆侧拱腰与被爆岩体之间被中导洞隔开，形成临空面，爆炸产生的应力波需经过绕行才能到达拱腰，损失了能量。

3.5 先行隧道衬砌的安全控制标准

根据文献[19]，C25混凝土的抗剪、抗拉和抗压强度设计值分别为1.8 MPa、1.3 MPa和12.5 MPa，考虑到混凝土的抗压强度远远大于抗拉强度和抗剪强度，本次计算主要分析后行隧道爆破荷载作用下先行隧道迎爆侧衬砌的拉应力和剪应力。图11为迎爆侧衬砌拱腰、拱脚和拱肩的最大拉应力和最大剪应力变化曲线。相对距离0 m为连拱段与小净距段的分界线，同时也是爆破开挖面。正距离方向为开挖方向。后述相对距离的含义均与此相同。

(a)拉应力

(b) 剪应力图11 迎爆侧衬砌应力衰减曲线Fig.11 Stress attenuation curve of the lining in head-burst side

从图11可以看出，最大拉应力发生在衬砌迎爆侧拱腰，为1.075 MPa，小于C25混凝土的抗拉强度设计值，不会对衬砌造成破坏。连拱段衬砌受到成洞区“空洞效应”的影响，振速衰减较慢。而小净距段拉应力衰减较快，至相对距离20 m处的拉应力已趋于平缓。从分布区域来看，爆破开挖面和隧道洞口附近的拉应力值最大。究其原因，当爆炸产生的应力波传播至迎爆侧洞壁的混凝土时，产生的拉伸反射作用使混凝土出现较大振速，同时拉应力也达到峰值。当应力波传播至隧道洞口混凝土时，受自由面的影响，应力波经过反射后产生拉伸波。由于混凝土的拉伸强度较低，拉伸波易对隧道洞口的衬砌产生拉伸破坏。剪应力的衰减规律与拉应力相似，较大值均出现在洞口段和爆破开挖面附近。最大剪应力出现在相对距离0 m处的迎爆侧拱脚，为0.913 MPa，小于C25混凝土抗剪强度设计值。

考虑到连拱段隧道开挖时，爆破振动对先行隧道侧导洞支护层的影响较大，根据侧导洞支护层的结构特点，选取代表性的控制节点如图12所示。连拱段侧导洞支护层的拉应力衰减曲线如图13所示。

图12 连拱段侧导洞支护层拉应力控制点布置图Fig.12 Tensile stress control point arrangement of the supporting in multi-arch segment pilot tunnel

图13 连拱段侧导洞支护层拉应力衰减曲线Fig.13 Tensile stress attenuation curve of the supporting in multi-arch segment pilot tunnel

由图13可知，侧导洞支护层的拉应力较大值主要分布在爆破开挖面和隧道洞口，这与衬砌迎爆侧拉应力的分布规律类似。最大拉应力出现在1#控制点，为0.61 MPa，其次为3#控制点，2#控制点拉应力值最小，最大值仅0.11 MPa。可以看出，相比衬砌迎爆侧的最大拉应力值，爆破振动对连拱段侧导洞支护层的影响较小。因此，后续的分析以先行隧道衬砌迎爆侧为主。

由衬砌迎爆侧的应力分析可知，C25混凝土抗拉强度设计值与最大拉应力的差值为0.225，远远小于抗剪强度设计值与最大剪应力的差值0.887。在爆破荷载作用下，混凝土衬砌首先产生拉伸破坏的可能性最大。由损伤力学可知，混凝土衬砌的拉伸破坏表现为物理力学参数的劣化[20]。因此，从物理力学参数劣化的角度确定临界振速在理论上是可行的。而混凝土衬砌的破坏主因是最大拉应力，符合最大拉应力理论[21]，即爆破振动产生的最大拉应力达到或超过混凝土的抗拉强度时，发生破坏。图14为先行隧道衬砌迎爆侧最大振速和最大拉应力的统计关系。

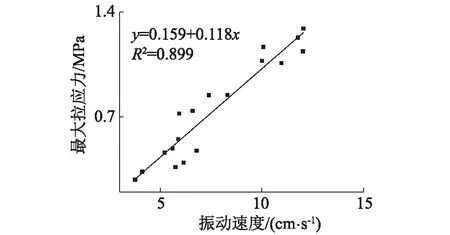
图14 最大振速和最大拉应力的关系Fig.14 Relationship between peak velocity and the maximum tensile stress

根据最大振速和最大拉应力的关系，有：

σ=-0.159+0.118V

(3)

式中：V为最大振速(cm/s)；σ为最大拉应力(MPa)。

取C25混凝土衬砌的抗拉强度设计值σ为1.3 MPa，代入公式(4)，可得，最大振速V为12.36 cm/s，即混凝土衬砌发生破坏的临界振速为12.36 cm/s。综合考虑隧道的地质条件，以及爆破振动对混凝土造成的累计损伤等，将爆破安全振速确定为10 cm/s，其值在爆破安全规程规定的允许范围内。

4 结 论

(1)先行隧道迎爆侧的爆破振速沿隧道掘进方向呈规律性变化，成洞区的爆破振速大于未开挖区。通过实测数据分析得到分岔隧道过渡段爆破地震波沿先行隧道中墙迎爆侧的传播规律。

(2)爆破振速与最大段药量并不成绝对正比关系。当段药量相差不太大的情况下，掏槽孔爆破产生的振动最大。因此，在预测爆破振动强度时，不仅要考虑最大段药量大小和爆源距离等因素，还应考虑炸药的安放位置，装药炮孔的集中度和炮孔的自由面条件等因素。

(3)当爆破荷载量级达到足以破坏衬砌时，先行隧道迎爆侧混凝土将先产生拉伸破坏，后产生剪切破坏。爆破荷载产生的拉应力最大值出现在迎爆侧拱腰，是最危险区域，而剪应力最大值则出现在迎爆侧的拱脚。施工过程中应及时监测，防止衬砌混凝土发生拉剪破坏，同时不能忽视隧道洞口自由面对应力波的反射作用。

(4)先行隧道衬砌迎爆侧的最大振速和最大拉应力之间存在线性关系，结合混凝土最大拉应力理论，可以得出后行隧道爆破荷载作用下先行隧道衬砌的临界破坏振速。

[ 1 ] 毕强, 吴金刚. 大跨分岔式隧道结构设计关键技术研究[J]. 隧道建设, 2011, 31(6): 668-677.

BI Qiang, WU Jingang. Study on key technologies for structural design of large-span forked tunnel[J]. Tunnel Construction，2011, 31(6): 668-677.

[ 2 ] 王者超, 李术才, 陈卫忠. 分岔隧道变形监测与施工对策研究[J]. 岩土力学, 2007, 28(4): 785-789.

WANG Zhechao, LI Shucai, CHEN Weizhong. Deformation monitoring of bifurcation tunnel and countermeasures of construction technologies[J]. Rock and Soil Mechanics, 2007, 28(4): 785-789.

[ 3 ] 蔚立元, 李术才, 郭小红, 等. 分岔隧道过渡段稳定性研究[J]. 中国公路学报, 2011, 24(1): 89-95.

YU Liyuan, LI Shucai, GUO Xiaohong, et al. Study of stability of transition scgmcnt for bifurcation tunnel[J]. China Journal of Highway and Transport, 2011, 24(1) 89-95.

[ 4 ] 时亚昕, 王明年, 李强. 爆破振动对双连拱隧道中墙的影响分析[J]. 岩土力学, 2007, 28(6): 1275-1279.

SHI Yaxin, WANG Mingnian, LI Qiang. Analysis of influence of blasting vibration on middle wall of a double-arch tunnel. [J]. Rock and Soil Mechanics, 2007, 28(6): 1275-1279.

[ 5 ] 贾磊, 解咏平, 李慎奎. 爆破振动对邻近隧道衬砌安全的数值模拟分析[J]. 振动与冲击, 2015, 33(11): 173-177.

JIA Lei, XIE Yongping, LI Shenkui. Numerical simulation for impact of blasting vibration on nearby tunnel lining safety. [J]. Journal of Vibration and Shock, 2015, 33(11): 173-177.

[ 6 ] 林从谋, 陈礼彪, 蒋丽丽, 等. 高速公路扩建大断面特小净距隧道爆破稳定控制技术研究[J]. 岩石力学与工程学报, 2010, 29(7): 1371-1378.

LIN Congmou, CHEN Libiao, JIANG Lili, et al. Research on blasting stability control technology of large-span highway with super-small clear spacing highway expansion project[J]. Journal of Rock Mechanics and Engineering, 2010, 29(7): 1371-1378.

[ 7 ] 朱正国, 孙明路, 朱永全, 等. 超小净距隧道爆破振动现场监测及动力响应分析研究[J]. 岩土力学, 2012, 33(12): 3747-3752.

ZHU Zhengguo, SUN Minglu, ZHU Yongquan, et al. Field monitoring on blasting vibration and dynamic response of ultra-small spacing tunnels[J]. Rock and Soil Mechanics, 2012, 33(12): 3747-3752.

[ 8 ] 李新平, 陈俊桦, 李友华, 等. 溪洛渡电站地下洞室群爆破地震效应的研究[J]. 岩石力学与工程学报, 2010, 29(3): 493-501.

LI Xinping, CHEN Junhua, LI Youhua, et al. Study of blasting seismic effects of underground chamber group in xiluodu hydropower station [J]. Journal of Rock Mechanics and Engineering, 2012, 29(3): 493-501.

[ 9 ] 姚强, 杨兴国, 陈兴泽, 等, 大型地下厂房开挖爆破振动动力响应数值模拟[J]. 振动与冲击, 2014, 33(6): 66-70.

YAO Qiang, YANG Xingguo, CHEN Xingze, et al. Numerical simulation of dynamic response of large underground powerhouse subjected to blasting vibration [J]. Journal of Vibration and Shock, 2014, 33(6): 66-70.

[10] LANGEFORS U, KIHLSTROM B. The modem technique of rock blasting[M]. New York：[s. n. ], 1973.

[11] 李云鹏, 艾传志, 韩常领, 等. 小间距隧道爆破开挖动力效应数值模拟研究[J]. 爆炸与冲击, 2007, 27(1): 75-81.

LI Yunpeng, AI Chuanzhi, HAN Changling, et al. Study on dynamics effect caused byblasting construction by numerical simulation for tunnels with small spacing[J]. Explosion and Shock Waves, 2007, 27(1): 75-81.

[12] 中华人民共和国国家标准编写组. GB6722-2014. 爆破安全规程[S]. 北京：中国标准出版社, 2014.

[13] 杨年华, 刘慧. 近距离爆破引起的隧道周边振动场[J]. 工程爆破, 2000, 6(2)： 6-10.

YANG Nianhua, LIU Hui. Vibration field at tunnel contour induced by a close-in blasting[J]. Engineering Blasting, 2000, 6(2)： 6-10.

[14] 张庆松, 李利平, 李术才, 等. 小间距隧道爆破动力特性试验研究[J]. 岩土力学, 2008, 29(10): 2655-2660.

ZHANG Qingsong, LI Liping, LI Shucai, et al. Experimental study of blasting dynamic vibration of closely adjacent tunnels[J]. Rock and Soil Mechanics, 2008, 29(10): 2655-2660.

[15] LSTC. LS-DYNA Keyoword user’s manual[M]. Livermore：Livermore Software Technology Corporation, 2007.

[16] YANG R, BAWDEN W F, KATSABANIS P D. A new constitutive model for blast damage[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 33(3): 345-354.

[17] 湖南省交通规划勘察设计院. 湖南省永顺至吉首高速公路第2合同段六月田隧道详细工程地质勘察报告[R]. 长沙, 湖南省交通规划勘察设计院, 2012.

[18] 杨国梁, 杨仁树, 车玉龙. 周期性爆破振动下围岩的损伤累积效应[J]. 煤炭学报, 2013, 38(增刊1): 25-29.

YANG Guoliang, YANG Renshu, CHE Yulong. Damage accumulative effect of surrounding rock under periodic blasting vibration[J]. Journal of China Coal Society, 2013, 38(Sup1): 25-29.

[19] 重庆交通科研设计院. JTGD70-2004. 公路隧道设计规范[S]. 北京：人民交通出版社, 2004.

[20] 胡英国, 卢文波, 陈明, 等, 岩体爆破近区临界损伤质点峰值震动速度的确定[J]. 爆炸与冲击, 2015, 35(4): 547-554.

HU Yingguo, LU Wenbo, CHEN Ming, et al. Determination of critical damage PPV near the blast hole of rock-mass[J]. Explosion and Shock Waves, 2015, 35(4): 547-554.

[21] 江见鲸, 冯乃谦. 混凝土力学[M]. 北京：科学出版社, 1991.