钢筋混凝土梁抗冲击性能研究的细观数值模拟方法

金 浏， 徐建东， 张仁波， 杜修力

(北京工业大学 城市减灾与防灾防护教育部重点实验室，北京 100124)

钢筋混凝土(RC)梁作为建筑结构主要的承重构件之一，除了要考虑正常的使用荷载外，还需考虑地震、冲击及爆炸等动力荷载的影响。此外，近几十年来世界范围内的爆炸冲击危害日益加剧，对建筑物的抗冲击性能设计提出了更高的要求。因此，对钢筋混凝土梁在冲击及爆炸等荷载作用下的力学性能进行研究具有重要的科学意义。

近年来，国内外学者对钢筋混凝土梁的抗冲击性能进行了大量落锤冲击试验。Kishi等[1]为了建立剪切失效的钢筋混凝土梁合理的抗冲击设计方法，对纵筋和剪跨比不同的无箍筋钢筋混凝土简支梁进行了落锤冲击加载试验；Fujikake等[2]通过落锤试验研究了落锤自由落体高度和纵筋配筋率对钢筋混凝土梁抗冲击性能的影响；许斌等[3]通过落锤试验研究了不同冲击锤重、冲击速度和冲击能量及二次冲击下钢筋混凝土梁的抗冲击行为；窦国钦等[4]通过落锤试验研究了不同冲击落锤质量和冲击能量下高强钢筋混凝土梁的抗冲击行为。

方秦等[5]研究结果表明在冲击初始阶段梁体加速度很大，此阶段冲击力主要由惯性力所抵抗，支座反力具有一定滞后性，随着落锤冲击速度的增加，梁的局部破坏趋于严重。此外，破坏截面上的剪应力有可能先于弯曲正应力达到其破坏值而使结构破坏形态由通常的弯曲破坏转变为剪切破坏。廖维张等[6]试验工作表明：用高强钢绞线网-高性能砂浆加固钢筋混凝土梁可显著提高其抗冲击性能。

由于试验设备约束及经济限制，开展大量的物理模型试验来探讨钢筋混凝土梁的抗冲击力学特性及破坏机理是不现实的，数值模拟已成为替代物理模型试验的一个有效途径。近年来，很多学者借助有限元方法模拟钢筋混凝土结构在冲击荷载下的响应。如：Cotsovos等[7]认为结构在不同荷载速率下的应变率效应是由于惯性力的影响，而不是材料的率敏感性，进而基于这个假设对钢筋混凝土梁的动态响应问题进行了数值仿真研究。Saatci等[8]基于应用弥散裂缝和扰动应力场模型的二维非线性有限元程序，模拟了冲击荷载作用下RC梁的剪切行为。Travaš等[9]基于连续介质力学和热力学不可逆理论，以弥散裂缝来考虑损伤和开裂，采用率敏感性的微平面模型，研究了素混凝土梁在落锤冲击下的动力性能。为了将混凝土材性试验数据更好的应用到冲击有限元模拟中，康翔杰等[10]分析了常用混凝土本构关系中的应变率参数作用特点，提出了一种基于构件试验结果线性插值的混凝土动态破坏面修正方法来减小构件响应计算误差。姜华等[11-12]采用弹塑性帽盖模型对Fujikake等的RC梁的冲击试验进行了数值模拟，该模型可以反映试验中观察到的混凝土材料的主要宏观行为。这些数值工作促进了钢筋混凝土梁抗冲击性能的认识，但大多数值模型中存在如下问题：①未考虑混凝土及钢筋的率效应；②假定钢筋/混凝土黏结完好，不考虑界面处的黏结-滑移行为。此外，这些数值模型均为模型尺度模型，难以揭示混凝土内部细观非均质性对钢筋混凝土梁冲击荷载下破坏行为的影响。

实际上，混凝土破坏行为与其细观结构密切关联[13]。混凝土是由砂浆及其内部随机分布的骨料、初始缺陷等组成的非均质复合材料，其内部组成的非均质性，导致了混凝土力学性质特别是强度的随机性和离散性。这种随机离散性将影响混凝土中裂缝的扩展路径和结构的破坏强度。

为更真实地描述钢筋混凝土梁在冲击荷载作用下复杂的破坏过程(尤其是加载局部区域的损伤破坏)，本文从细观角度出发，考虑混凝土非均质性，认为混凝土是由骨料颗粒、砂浆基质以及界面过渡区(ITZ)组成的三相复合材料，将钢筋“嵌入”至混凝土试件中，结合能反映材料应变率效应的本构关系模型，建立了钢筋混凝土梁抗冲击力学行为研究的细观尺度数值模型。将细观数值结果与宏观模拟结果及Fujikake试验[2]结果进行对比分析，验证了提出的细观数值模拟方法的可靠性。进而在此基础上，研究了落锤冲击速度对钢筋混凝土梁的动力响应的影响。

1 试验概况介绍

本文拟对日本国防研究所Fujikake等开展的钢筋混凝土梁落锤冲击试验进行了宏/细观有限元数值研究。Fujikake等试验模型及概况如下：

试验梁截面尺寸及配筋情况如图1所示，梁体受拉侧和受压侧均为2根直径为16 mm的带肋钢筋，单侧配筋截面积为397 mm2，屈服强度为426 MPa，箍筋直径为10 mm，布置间距75 mm，屈服强度为295 MPa。

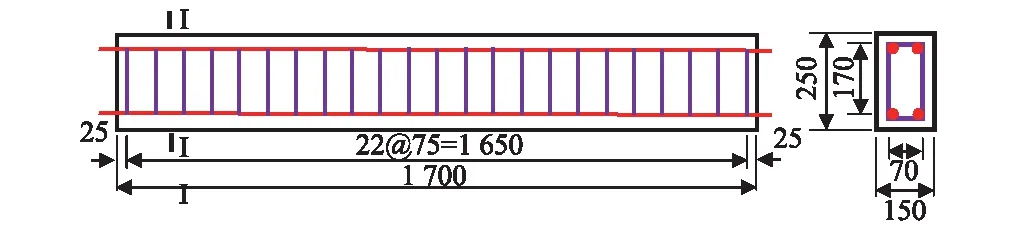
图1 试件截面尺寸及配筋(mm)Fig.1 Cross-section size and rebar arrangement (mm)

试验中采用的混凝土配合比如表1所示，试验在试件浇注并养护70天后进行，测得的单轴抗压强度为42.0 MPa。试验中浇注4个相同尺寸和配筋的梁，供4个工况使用，各工况如表2所示。

表1 混凝土配合比

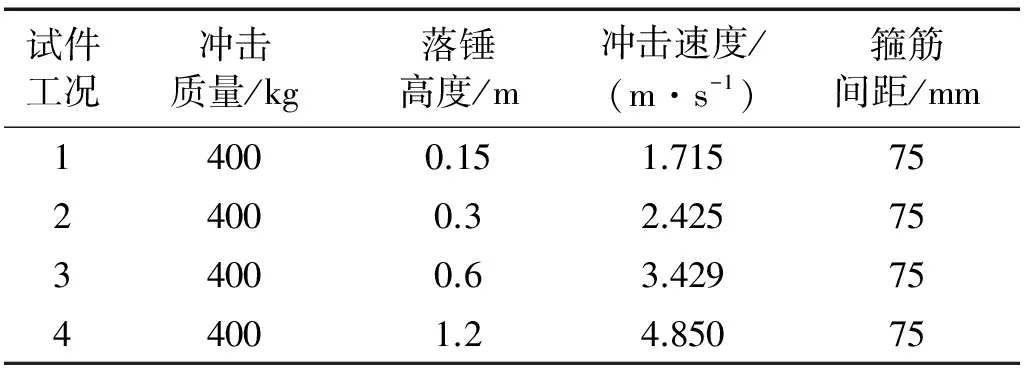
表2 钢筋混凝土梁落锤冲击试验工况

采用图2所示的冲击试验装置，总质量为400 kg的落锤从不同高度(落锤高度H分别为0.15 m，0.3 m，0.6 m和1.2 m)自由落体冲击钢筋混凝土梁跨中位置，冲头为直径90 mm的半球形，材料为钢材。试件被放置在只允许转动而不能平动的特定支撑装置上，其净跨为1.4 m。采用动态力传感器记录钢筋混凝土梁与落锤之间的冲击力，激光位移传感器采集钢筋混凝土梁跨中位移，采样频率均为100 kHz。

2 钢筋混凝土梁细观数值模型

2.1 细观混凝土梁有限元几何模型建立

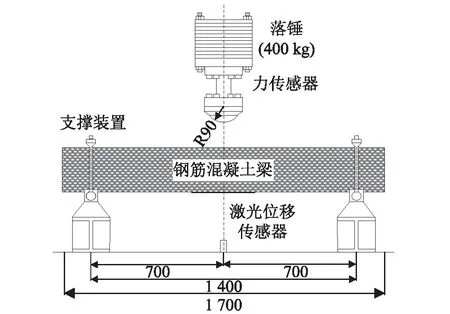
图2 落锤冲击试验装置(mm)Fig. 2 Drop hammer impact test setup(mm)

在细观层次上，常将混凝土看作由骨料颗粒、砂浆基质以及两者之间的界面过渡区(ITZ)组成的三相非均质复合材料[14-16]。参考Zhou等[17]的工作，骨料颗粒假定为球形，体积分数为30%，最小等效粒径为10 mm，最大等效粒径为30 mm。采用经典的“取-放”法[13]将骨料颗粒投放在砂浆基质中，并将骨料周围的薄层设定为界面过渡区(厚度为5 mm)，生成混凝土三维细观数值模型。将有限元网格投影到该骨料结构上，然后根据各相组分在网格中的位置判定单元类型(如：骨料单元、砂浆基质单元及界面单元)，并依单元类型赋予相应的材料特性。在此基础上，插入钢筋笼，生成如图3所示的三维细观钢筋混凝土梁数值模型。

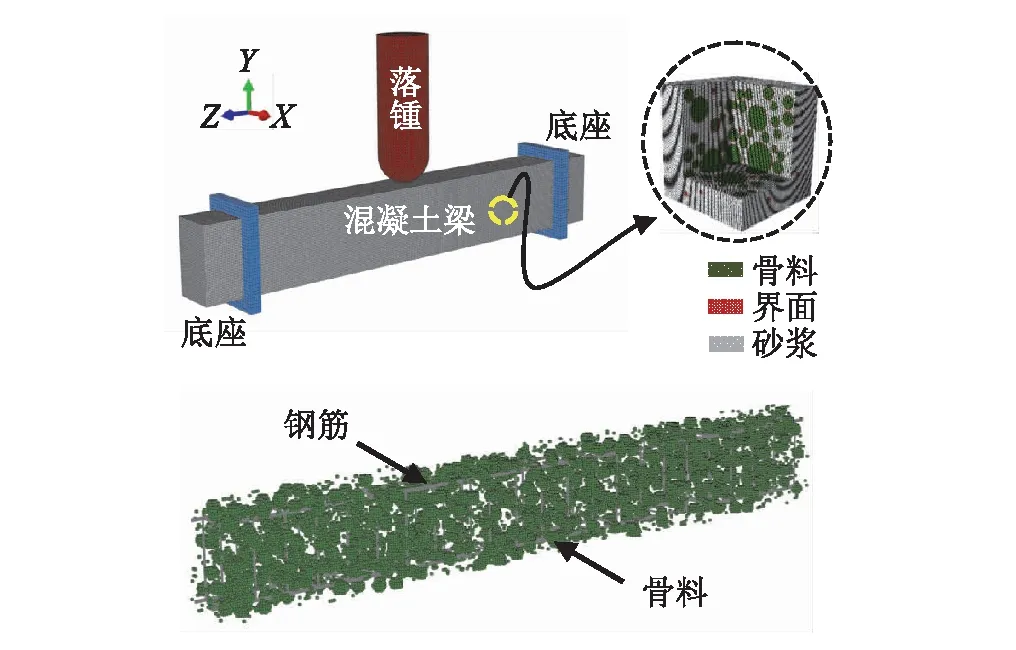
图3 钢筋混凝土梁细观力学分析模型Fig. 3 The mesoscopic mechanics analysis model of reinforced concrete beam

对于混凝土细观组分单元，采用8节点六面体线性单元来进行划分网格，单元网格尺寸为5 mm，全梁共划分510 000个实体单元；对于钢筋网，采用梁单元来进行离散，以考虑钢筋的抗弯承载力。

这里需要说明的是，界面过渡区的实际厚度约为20～50 μm，但考虑到计算量的限制，单元网格尺寸及界面相的尺寸设定为5 mm。

另外，由于钢筋与混凝土相互作用力学行为的高度复杂性，目前尚未得到统一的理论与力学模型，且在冲击荷载作用下，钢筋/混凝土间界面的力学行为(黏结及滑移等非线性)将变得尤为复杂(即：存在应变率效应)。鉴于此，为简化钢筋与混凝土相互作用力学行为以及提高模型的计算效率，本文暂假定钢筋与混凝土黏结完好，两者界面间不产生分离及滑移等行为，将钢筋“嵌入”混凝土中。

2.2 材料组分本构关系及力学参数确定

研究发现[17-18]，骨料强度较高，即使在冲击过程中一般不会发生破坏，因此骨料只考虑弹性变形，为弹性体。混凝土(宏观模型)、砂浆基质和界面相则采用Lee等[19]提出的塑性损伤模型来描述其力学行为，该本构模型的核心是假定混凝土的破坏形式是拉伸断裂和压缩破坏，并由各向同性的损伤变量来分别表征其拉伸断裂和压碎(crushing)破坏行为。关于该塑形损伤本构关系模型的详细说明，见Du等的研究。

钢筋材料较均匀，见Cotsovos的研究，这里采用理想弹塑性本构模型描述其力学行为。

混凝土材料及其细观组分、钢筋的力学参数等如表3所示，各参数的物理意义详见Du等的研究。需要说明的是，骨料和砂浆基质的力学参数由试验中实测数据，而对于界面过渡区的力学参数(包括材料弹性模量和强度)为反复试算获得的选取值(这里假定，砂浆基质单轴抗压强度为单轴拉伸强度的10倍)，其它力学数据为默认值。采用表3所示的界面力学参数时，由混凝土立方体单轴拉/压数值试验得知混凝土的单轴压缩强度为41.8 MPa，与试验实测强度42 MPa接近。说明本文通过反演法得到的混凝土细观尺度力学分析模型中各细观组分的力学参数取值是合理的。这些力学参数将运用于下文的关于钢筋混凝土梁的数值模拟中。

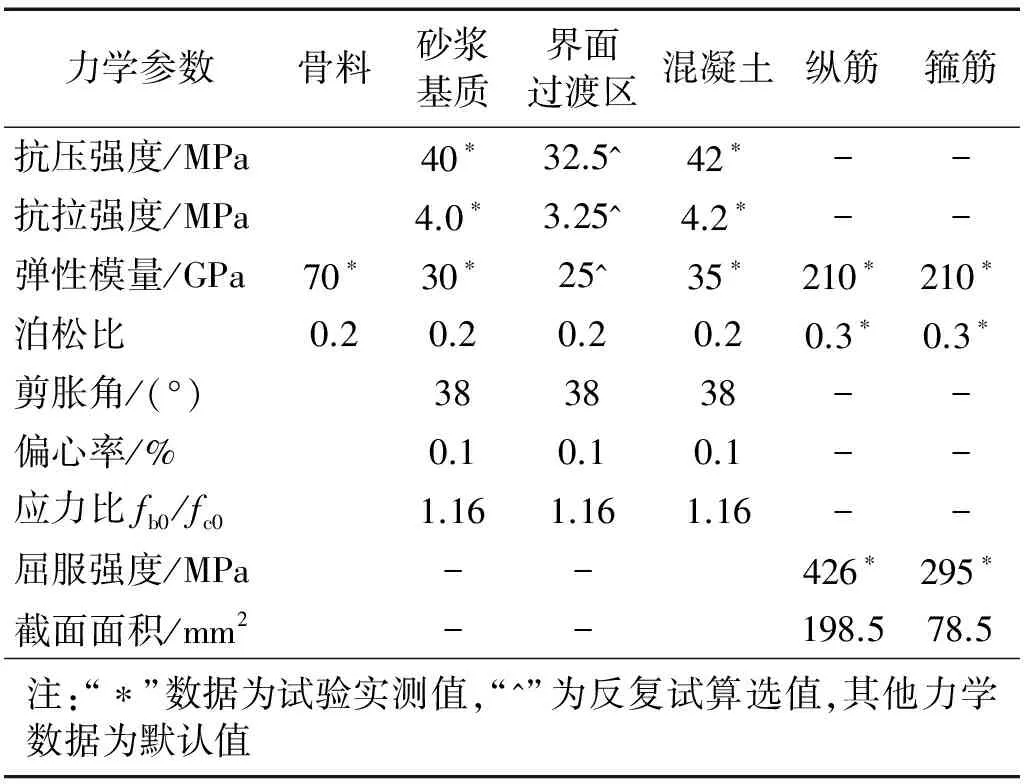
表3 混凝土细观组分及钢筋力学参数

2.3 材料力学性能的率效应

大量的试验及理论研究均表明混凝土及水泥基材料具有明显的率敏感性[20]。相关研究[21-22]表明：相比于抗拉及抗压强度，混凝土的其它力学参数如弹性模量、泊松比、能力耗散能力及峰值应变等率敏感性较弱。鉴于此，本文仅考虑材料强度的放大行为，即细观组分的应变率效应用其强度的增大系数DIF(即动态强度/静态强度)来表示。

采用CEB规范中给出的公式来表征混凝土抗压强度的放大效应(CDIF)，即[23]：

(1)

对于混凝土拉伸强度放大行为(TDIF)，这里采用修正的CEB模型[24]来描述：

(2)

Grote等研究表明水泥基复合材料动态力学行为与混凝土类似，故而对于砂浆基质及界面过渡区，可采用耦合上述强度应变率效应的塑性损伤本构关系来描述其在冲击荷载作用下的力学特性。

实际上，钢筋在动态加载下必然存在应变率效应，并且纵筋会显著影响构件的抗弯刚度，因而会影响构件在冲击荷载作用下的位移响应[25-26]。这里，同田力和Yuen等的研究，对于钢筋(纵筋和箍筋)采用随动双线性弹塑性模型，其应变率效应通过Cowper-Symonds模型[27]考虑，钢筋的屈服应力σy为：

(3)

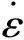
塑性硬化模量Ep为：

Ep=EEt/(E-Et)

(4)

式中：E为初始弹性模量；Et为塑性切线模量。

2.4 边界/加载条件

数值模拟中，试验梁被“绑定”在底座上，即两者间为理想黏结，如图3所示。

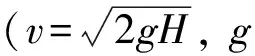
3 冲击荷载作用下钢筋混凝土梁破坏行为

为说明本文提出的细观尺度数值分析方法的合理性和可靠性，基于上述建立的细观数值方法对Fujikake等的试验开展数值对比研究。另外，同时建立了钢筋混凝土梁抗冲击动态行为研究的宏观尺度数值分析模型，即：不考虑混凝土材料内部的非均质性，为均匀体。宏观模型中，混凝土亦采用塑性损伤本构模型来描述，参数详见表3。

3.1 破坏模式

图4给出了钢筋混凝土梁在冲击加载下破坏模式(包括试验结果、宏观及细观尺度模拟结果)。从图4可以看出，在落锤冲击作用下，混凝土梁均产生了剪切斜裂缝，斜裂缝从冲击处向下45°方向扩展，但试件主要破坏裂缝是跨中部位沿梁高方向的垂直裂缝，因而试件以弯曲破坏为主。随着冲击速度的增大，剪切斜裂缝愈加明显，构件逐渐趋于弯剪破坏。试件的局部损伤也随着冲击速度的增大趋于严重，并产生了混凝土的局部剥落。当冲击速度较低时，混凝土裂缝较细而密，没有产生贯通裂缝，随着冲击速度的增大，损伤区域的裂缝宽度增大，裂缝数量增多并产生贯通裂缝。

对比细观与宏观的数值模拟结果发现，宏观模型裂缝较集中，并且裂缝宽度更大；细观模型考虑了混凝土材料的非均质性，由于各组分材料力学性能的差异，损伤裂缝扩展过程中避开了强度较高的骨料区域，使得细观模型的裂缝更加曲折和分散，裂缝扩展路径更加复杂。总体来说，宏/细观尺度数值模型均能较好的模拟钢筋混凝土梁的破坏模式。

相对而言，与试验结果对比知，细观模型结果与试验结果吻合更好，验证了本文提出的细观数值模拟方法的可行性和准确性。

图5展示了最终破坏时细观数值模型内部损伤破坏分布和钢筋的应变云图。其中A-A，B-B分别为距左侧支座1/4跨度处与跨中处界面损伤剖面图。由于界面过度区是最为薄弱的区域，混凝土的破坏(损伤或裂缝)一般最先出现在该区域，且混凝土中裂缝通常绕过高强度的骨料颗粒，沿着界面及砂浆基质扩展。从图5(a)可以发现由于界面过渡区的存在，混凝土内部损伤比外部更加严重，而且随着冲击速度的提高，混凝土内部损伤区域面积增大。对比A-A与B-B剖面，可见跨中损伤更加严重，而且随着冲击速度的增加，混凝土梁冲击点处与梁底损伤部位逐渐贯通，混凝土梁内部产生严重破坏。由图5(b)所示的钢筋应变云图可知，随着冲击速度的增加，钢筋的最终残余应变逐渐增大，其中跨中受拉区域的钢筋应变最大。

图4 钢筋混凝土梁冲击加载下破坏模式(试验、细观和宏观数值模拟结果)Fig. 4 Final failure patterns of the RC beams subjected to impact loading (Test results, meso-and macro-scale simulation results)

图5 钢筋混凝土梁内部破坏和钢筋应变分布Fig. 5 Internal damage of reinforced concrete beams and strain distribution of steel bar

3.2 冲击荷载下梁裂缝发展过程

图6(a)给出了工况-4(即落锤高度H为1.2 m)中混凝土梁在冲击荷载作用下的冲击力、支座反力和跨中位移随时间的变化过程，其中支座反力为两端支座反力的合力。图6(b)为各个关键时刻钢筋混凝土梁的变形过程。通过图6可以更加深入地理解混凝土梁在冲击荷载作用下各时程曲线的对应关系和混凝土梁的裂缝的开展过程。

从图6(a)可以看出，当落锤接触混凝土梁的瞬间即产生接触力，冲击力瞬时增大，在1 ms左右达到冲击力峰值，支座反力比冲击力滞后大约0.5 ms，由于混凝土梁的惯性效应，混凝土梁两端产生翘曲，从而使支座反力产生一个较小的负值，之后支座反力也迅速增加，滞后冲击力1.5 ms达到峰值，支座反力峰值约是冲击力峰值的3/4。跨中位移时程曲线与支座反力时程曲线起始时刻相同。对比三条曲线发现，在冲击力和支座反力震荡的过程中跨中位移持续增加，整个冲击过程历时约40 ms。

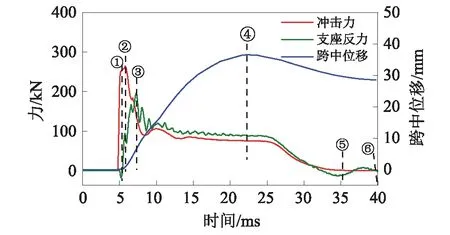
(a) 冲击力、支座反力和跨中位移时程曲线

(b) 冲击荷载下混凝土梁应变发展过程图6 混凝土梁冲击荷载动力响应(工况4)Fig. 6 Dynamic response of concrete beam (test 4)

从图6(b)混凝土梁的破坏过程可以发现：①在冲击力达到峰值以前混凝土梁受冲击部位即产生第一条沿梁高方向的贯通裂缝，该裂缝起始于混凝土受拉侧，向混凝土梁冲击部位发展；②当冲击力达到峰值时，混凝土梁在冲击部位产生许多剪切斜裂缝，该裂缝从冲击部位向梁底面扩展，同时开始出现多条新的弯曲裂缝；③当支座反力达到峰值时混凝土梁的破坏模式基本形成，呈现明显的弯剪破坏，此时支座处混凝土也产生局部压碎；④当跨中位移达到峰值时，混凝土梁裂缝进一步开展，其微小裂缝联通，使裂缝加宽加深。支座处混凝土破坏严重，产生贯通裂缝；⑤当冲击力消失时，混凝土裂缝区域轻微增大，梁跨中变形减小；⑥试件完全破坏时混凝土裂缝分布基本形成，弹性变形恢复，仅剩下残余变形。

3.3 冲击力时程反应

从图7给出的各个试件的冲击力时程曲线中可以看出，冲击力在很短的时间内达到一个明显的峰值，然后迅速下降，形成一个明显的主峰，之后产生一系列震荡形成若干小波峰，最后趋近与零。在冲击力达到峰值以前，数值模拟结果与试验吻合较好，在达到峰值以后的震荡阶段，模拟值与试验结果产生一定误差。比较不同落锤速度下的冲击力时程曲线发现，当冲击质量一定的情况下，冲击力的峰值随着冲击速度的提高而增大，冲击力持续时间也随着冲击速度的提高而增加。对比试验结果不难发现：在低速加载作用下，细观数值模型获得的冲击力的持续时间与试验结果存在一定误差，而当落锤冲击速度提高以后，冲击力持续时间与试验结果吻合较好。

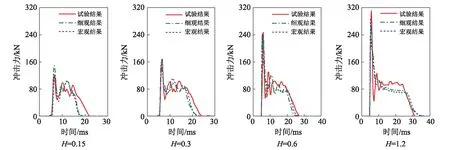
图7 冲击力时程曲线对比(试验、细观和宏观数值模拟结果)Fig. 7 Comparison of impact force time history curves (Test results, meso-and macro-scale simulation results)

3.4 跨中位移反应

从图8中可知，跨中位移峰值和残余位移均随冲击速度的增大而增加。宏观和细观数值分析模型均可以大致地反映钢筋混凝土梁的跨中变形过程。总体来说，跨中变形的起始阶段与试验结果吻合较好，获得的跨中位移峰值与试验结果均接近。

从图8还可以看出，未考虑钢筋应变率效应 (细观结果2和宏观结果2)时，数值模拟获得的跨中位移存在一定的滞后性(尤其对于落锤高度为1.2 m工况)，且落锤高度越大，初始冲击速度越大，钢筋的率效应影响更为明显。而考虑钢筋应变率效应(细观结果1和宏观结果1)时获得的跨中位移时程曲线则与试验结果吻合良好(如图8所示)，且相比于宏观模型模拟结果，细观数值模拟结果与试验结果更为吻合。简言之，冲击行为数值计算中应考虑钢筋的率效应行为。

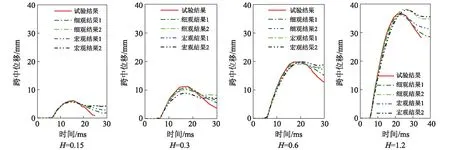
图8 跨中位移时程曲线对比(试验、细观和宏观数值模拟结果)Fig. 8 Comparison of Mid-span displacement time history curves (Test results, meso-and macro-scale simulation results)

纵使如此，不管对于宏观或细观模型，即使考虑钢筋材料的应变率效应时，数值模拟获得的残余变形均较试验结果依然略微偏大。造成该结果偏大的可能原因包括：①本文混凝土材料采用的塑性损伤模型实际上为一维本构关系模型，将其简单的扩展运用到复杂的梁抗冲击行为模拟中时，其是否能合理真实地描述混凝土材料复杂的塑性变形能力还需进一步深入探讨；②未考虑钢筋/混凝土界面的非线性黏结-滑移行为，亦可能是导致数值计算获得的残余变形偏大的另一原因。

3.5 支座反力反应

Fujikake等试验中未给出试验过程中的支座反力，这里仅对宏细观数值模拟结果的支座反力进行对比分析，如图9所示。宏细观数值模型获得的支座反力基本重合，支座反力峰值接近，只是由于材料的不均匀性，细观数值模型中的支座反力时程曲线更加曲折。从图中可以看出在冲击开始瞬间，各试件的支座反力均出现瞬时向下的较小的负值，且这个负值的绝对值随着冲击速度的提高而增大。当支座力达到负向峰值后，随即迅速增大到正向峰值，随后支座反力的时程曲线表现出波动现象，当冲击力消失后，支座反力由于结构的自由振动而产生一系列幅值相同的震荡。随着冲击速度的提高，支座反力的峰值逐渐增大，支座反力的持续时间也在增加。支座反力时程曲线变化规律与许斌等的研究相似，因此也验证了本文细观数值模拟结果的可靠性。

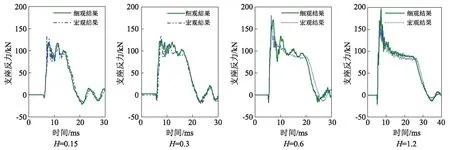
图9 宏观与细观模型支座反力的时程曲线对比Fig. 9 Comparison of support reaction time history curves of macroscopic and mesoscopic model

4 细观尺度数值方法的讨论

上文建立了钢筋混凝土构件冲击力学行为模拟的细观尺度数值模拟方法，这里将对该方法进行讨论分析。

相比于宏观模型，细观尺度分析模型需要对骨料、界面及砂浆基质进行网格划分，因而将占据更多的计算资源；另外细观组分材料力学参数的确定实际上亦增加了模型的复杂性。

虽然如此，混凝土宏观力学性能的非线性本质上根源于其细观组成的非均质性。相比于宏观尺度分析模型，细观尺度分析模型真实的展示了混凝土内部的微-细观结构组成，能更真实、更细致的描述外荷载作用下混凝土内部的损伤破坏过程，因而可以从本质上揭示动态冲击荷载作用下混凝土的破坏机制。

正如上文所述，对比本文宏观及细观尺度模型的数值模拟结果(图4,7～9)，可以看出，细观尺度数值模拟结果与试验结果吻合更好，尤其是在梁破坏模式及跨中残余变形特性的模拟方面。

需要说明的是，本文建立的混凝土细观尺度数值模型中，骨料的形状设定为球形体，亦没有考虑动态冲击荷载作用下骨料的断裂破坏行为。因此，后续工作中依然需要对其进行深入的研究，如可借助于CT图像扫描方法[14, 29]来建立混凝土构件。

5 结 论

本文以Fujikake等试验中的钢筋混凝土梁为研究对象，考虑了混凝土材料的非均质性和应变率效应，建立了钢筋混凝土梁抗冲击力学性能研究的细观尺度数值分析模型与方法，进而研究了落锤速度对钢筋混凝土梁抗撞击力学性能的影响规律。此外，还将本文的细观数值模拟结果与宏观模型和试验结果进行了对比分析，验证了细观尺度数值方法的合理性和优越性。根据数值模拟结果，可得到如下结论：

(1) 建立的细观尺度数值分析模型，不仅能很好地描述钢筋混凝土梁的破坏模式，还可以很好的反映梁的冲击力、跨中变形及支座反力等。

(2) 与宏观力学分析模型相比，三维细观尺度力学分析模型能充分体现混凝土材料的非均质性，能够细致地描述钢筋混凝土梁的裂缝发展及破坏过程，且获得的模拟结果与试验结果更为吻合。

(3) 在落锤质量一定的情况下，随着冲击速度的提高，冲击力峰值、最大跨中位移和支座反力峰值都有明显的提高。

需要说明的是，针对动态加载下钢筋/混凝土相互作用问题，本文暂未考虑钢筋与混凝土之间黏结、滑移与分离等非线性力学行为。这种简单粗糙的处理方法，势必将会对钢筋混凝钢筋混凝土梁抗冲击行为产生影响。因此，后续的研究工作中将继续完善本文的数值分析模型与方法。

[ 1 ] KISHI N, MIKAMI H, MATSUOKA K G, et al. Impact behavior of shear-failure-type RC beams without shear rebar[J]. International Journal of Impact Engineering, 2002, 27(9): 955-968.

[ 2 ] FUJIKAKE K, LI B, SOEUN S. Impact response of reinforced concrete beam and its analytical evaluation[J]. Journal of Structural Engineering, 2009, 135(8): 938-950.

[ 3 ] 许斌，曾翔. 冲击荷载作用下钢筋混凝土梁性能试验研究[J]. 土木工程学报, 2014, 47(2): 41-51.

XU Bin, ZENG Xiang. Experimental study on the behaviors of reinforced concrete beams under impact loadings[J].China Civil Engineering Journal, 2014, 47(2): 41-51.

[ 4 ] 窦国钦, 杜修力, 李亮. 冲击荷载作用下高强钢筋混凝土梁性能试验[J]. 天津大学学报(自然科学与工程技术版), 2014, 47(12): 1072-1080.

DOU Guoqin, DU Xiuli, LI Liang. Experimental study on the behavior of high strength reinforced concrete beams under impact load[J]. Journal of Tianjin University(Science and Technology), 2014, 47(12): 1072-1080.

[ 5 ] 方秦, 吴平安. 爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J]. 计算力学学报, 2003, 48(1): 39-42.

FANG Qin,WU Pingan. Analysis of the main factors affecting the failure mode of RC beams under blast loading[J].Chinese Journal of Computational Mechanics, 2003, 48(1): 39-42.

[ 6 ] 廖维张, 张伟, 田志敏.高强钢绞线网-高性能砂浆加固钢筋混凝土梁抗冲击性能试验研究[J]. 振动与冲击, 2014, 33(12): 200-206.

LIAO Weizhang, ZHANG Wei, TIAN Zhimin. Tests for impact resistance properties of RC beams strengthened with high strength steel wire mesh and high performance mortar [J]. Journal of Vibration and Shock, 2014, 33(12): 200-206.

[ 7 ] COTSOVOS D M. Behavior of RC beams subjected to high rates of concentrated loading[J]. Journal of Structural Engineering, 2008, 134(12): 1839-1851.

[ 8 ] SAATCI S, VECCHIO F J. Nonlinear finite element modeling of reinforced concrete structures under impact loads[J]. ACI Structural Journal, 2009, 106(5): 717-725.

[10] 康翔杰，刘艳辉，许浒，等. 低速冲击碰撞有限元分析中混凝土动态破坏面修正方法[J]. 工程力学, 2016, 33(3): 135-142.

KANG Xiangjie, LIU Yanhui, XU Hu, et al. A modified method for defining concrete dynamic failure surface under low-speed impact finite element analysis[J]. Engineering Mechanics, 2016, 33(3): 135-142.

[11] 姜华，贺拴海，王君杰. 钢筋混凝土梁冲击试验数值模拟研究[J]. 振动与冲击, 2012, 31(15): 140-145.

JIANG Hua, HE Shuanhai, WANG Junjie. Numerical simulation of the impact test of reinforced concrete beams[J]. Journal of Vibration and Shock, 2012, 31(15): 140-145.

[12] JIANG H, WANG X, HE S. Numerical simulation of impact tests on reinforced concrete beams[J]. Materials and Design, 2012, 39: 111-120.

[13] 杜修力，韩亚强，金浏，等. 骨料空间分布对混凝土压缩强度及软化曲线影响统计分析[J]. 水利学报, 2015, 46(6): 631-639.

DU Xiuli, HAN Yaqiang, JIN Liu, et al. The spatial distribution of aggregate concrete compressive strength and softening curve statistical analysis[J].Journal of Hydraulic Engineering, 2015, 46(6): 631-639.

[14] HUANG Y J, YANG Z J, CHEN X W, et al. Monte carlo simulations of meso-scale dynamic compressive behavior of concrete based on X-ray computed tomography images [J]. International Journal of Impact Engineering, 2016, 97: 102-115.

[15] YAN P, ZHANG J H, FANG Q, et al. 3D numerical modelling of solid particles with randomness in shape considering convexity and concavity [J]. Powder Technology, 2016, 301: 131-140.

[16] 金浏，杜修力. 钢筋混凝土构件细观数值模拟分析[J]. 水利学报, 2012, 43(10): 1230-1236.

JIN Liu, DU Xiuli. Meso numerical simulation of reinforced concrete members[J]. Journal of Hydraulic Engineering, 2012, 43(10): 1230-1236.

[17] ZHOU X Q, HAO H. Mesoscale modeling of concrete tensile failure mechanism at high strain rates [J]. Computers and Structures, 2008, 86(21/22): 2013-2026.

[18] DU Xiuli, JIN Liu, MA Guowei. Numerical simulation of dynamic tensile-failure of concrete at meso-scale [J]. International Journal of Impact Engineering, 2014, 66: 5-17.

[19] LEE J, FENVES G L. Plastic-damage model for cyclic loading of concrete structures[J]. ASCE Journal of Engineering Mechanics, 1998, 124(8): 892-900.

[20] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization[J]. International Journal of Impact Engineering, 2001, 25(9): 869-886.

[21] BISCHOFF P H, PERRY S H. Compressive behavior of concrete at high strain rates [J]. Materials and Structures, 1991, 24(6): 425-450.

[22] ZHAO H, GARY G. On the use of SHPB techniques to determine the dynamicbehavior of materials in the range of small strains [J]. International Journal of Solids and Structures, 1996, 33(23):3363-3375.

[23] Comite Euro-International D B. CEB-FIP model code 1990[S]. Trowbridge, Wiltshire, UK: Redwood Books, 1993.

[24] MALVAR L J, ROSS C A. Review of strain rate effects for concrete in tension [J]. ACI Materials Journal, 1998, 95(6): 735-739.

[25] 田力，朱聪，王浩，等. 碰撞冲击荷载作用下钢筋混凝土柱的动态响应及破坏模式[J]. 工程力学, 2013(2): 150-155.

TIAN Li, ZHU Cong, WANG Hao, et al. Dynamic response and failure modes of RCcolumns under impact[J].Engineering Mechanics, 2013(2): 150-155.

[26] 李敏，李宏男. 建筑钢筋动态试验及本构模型[J]. 土木工程学报, 2010, 43(4): 70-75.

LI Min, LI Hongnan. Dynamic test and constitutive model for rein forcing steel[J]. China Civil Engineering Journal,2010, 43(4): 70-75.

[27] YUEN S C K, NURICK G N. Experimental and numerical studies on the response of quadrangular stiffened plates. Part I: subjected to uniform blast load [J]. International Journal of Impact Engineering, 2005, 31(1): 55-83.

[28] BHATTI A Q, KISHI N, MIKAMI H, et al. Elasto-plastic impact response analysis of shear-failure-type RC beams with shear rebars[J]. Materials and Design, 2009, 30(3): 502-510.

[29] HUANG Y, YAN D, YANG Z, et al. 2D and 3D homogenization and fracture analysis of concrete based on in-situ X-ray Computed Tomography images and Monte Carlo simulations[J]. Engineering Fracture Mechanics, 2016, 163: 37-54.