带轴向运动柔性梁附件航天器的刚-柔耦合动力学分析
程 顺, 沈振兴, 崔 涛, 李慧剑
(燕山大学 河北省重型装备与大型结构力学可靠性重点实验室,河北 秦皇岛 066004)
当前航天器正面向大型化、复杂化和精密化方向发展,为了提高大型空间结构的使用寿命、运行精度和工作效率,考虑航天器主体和所带轴向运动柔性梁的刚-柔耦合作用是十分有必要的。截至目前为止,考虑柔性梁轴向运动、横向振动以及航天器姿态扰动三者之间相互耦合的文献非常少。
Tabarrok等[1]引入新的动力学模型,对轴向运动梁进行动力学分析,利用牛顿第二定理和拉格朗日法推导出模型系统的运动方程,采用假设模态法离散得到一个含有时变系数矩阵的偏微分方程;沈少萍等[2]利用动量矩定理推导出末端带集中质量的可伸缩柔性附属结构与航天器姿态耦合动力学方程,研究带末端质量附件的轴向伸展运动对航天器姿态及对附件横向振动的影响;Wang等[3]运用广义Hamilton原理推导出轴向运动Euler-Bernoulli梁的运动控制偏微分方程,采用假设模态法求解系统的运动方程;刘宁等[4]将弹炮发射系统简化为移动质量作用下的轴向运动悬臂梁系统,推导出轴向运动梁横向振动方程,采用修正Galerkin法得到以模态坐标表示的二阶时变常微分方程组,通过Newmark法对方程组进行求解; Park等[5]对轴向可伸缩梁进行振动分析,同时考虑纵向和横向位移,推导出的纵向运动方程是线性的,与横向运动不耦合,推导出的横向运动方程是非线性的,与纵向运动耦合;Shen等[6]采用绝对节点坐标法研究航天器结构在耦合热-结构分析和非耦合热-结构分析情况下的动力学响应;Yang等[7]考虑轴向运动梁纵向-横向振动的耦合,采用Galerkin截断法将运动控制偏微分方程截断为耦合的非线性常微分方程组,运用多尺度法求解运动方程;陈红永等[8]针对 Galerkin截断法在计算轴向受压运动梁的固有特性时,低阶频率误差较大的问题,通过引入轴向力作用对试函数进行改进,分析两端固支和固支-自由边界条件下Timoshenko运动梁在轴向压力作用下振动特性;闫业毫等[9]利用有限元方法对柔性梁进行离散,采用 Lagrange方程建立柔性梁的刚-柔耦合动力学方程,研究柔性梁的大范围运动和变形运动的相互耦合机理,比较零次模型、一次耦合模型、精确模型的差异,探讨各种模型的适用性;孙述鹏等[10]针对带大型太阳能帆板的航天器,使用蜂窝板对太阳能帆板进行建模,利用Hamilton原理建立了航天器刚柔耦合动力学方程,分析了刚柔耦合非线性项及系统参数对航天器固有特性和热诱发动力学响应的影响。
以上大多数研究模型是考虑了航天器主体与柔性附属结构之间的刚柔耦合作用,却没有考虑柔性附属结构的轴向运动,或者考虑柔性附属结构轴向运动,却尚未考虑航天器主体与柔性附属结构之间的刚-柔耦合作用。而刚柔耦合模型建模方法根据参考坐标的选取不同,基本上可分为3种[11]:浮动坐标系法、随转坐标系法和惯性坐标系法。其中浮动坐标系法是将多体动力学与结构力学相结合的方法,这种方法使多体动力学软件扩展应用于柔性多体系统,可以充分利用模态技术,是目前柔性多体系统建模使用最广泛的方法。
本文主要通过浮动坐标系法[11]建立航天器主体-轴向运动柔性梁刚-柔耦合系统的动力学模型,考虑轴向运动柔性梁与航天器主体之间的耦合作用,分析航天器主体半径、航天器主体面密度和柔性运动梁轴向速度对柔性梁横向振动以及航天器姿态角的影响。
1 模型建立
本文以带有大型挠性天线的航天器为主要研究对象,首先建立研究对象的简化动力学模型,在建模过程中,作如下假设:
(1) 航天器在近地轨道上运行,忽略其所受重力;
(2) 航天器主体简化为圆柱形刚体,为研究方便,航天器只作单轴转动;
(3) 大型挠性天线简化为满足Euler-Bernoulli梁理论的轴向运动柔性梁,其长度远远大于宽度和厚度,线密度均匀,无需考虑转动惯量和剪切变形的影响,仅考虑柔性梁的横向弯曲振动。
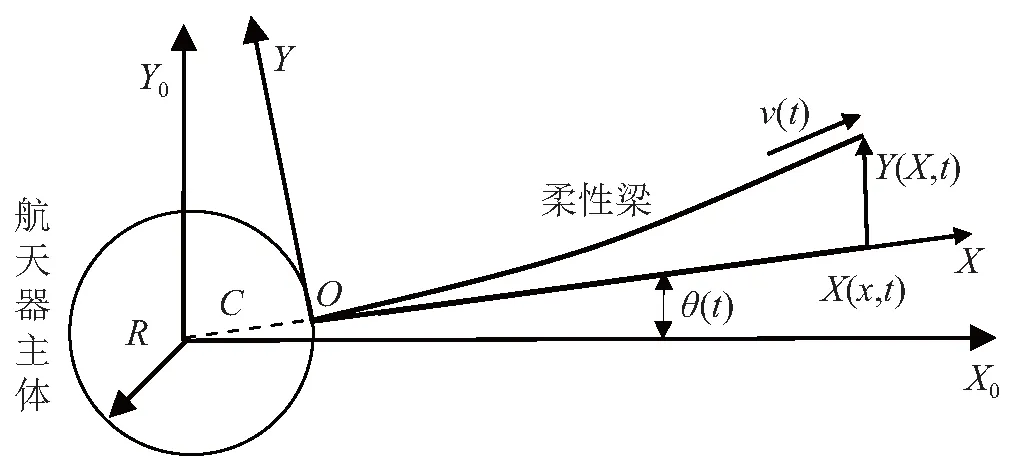
图1 航天器主体-轴向运动柔性梁刚-柔耦合模型Fig.1 The rigid-flexible coupling model of the spacecraft body and axially moving flexible beam
如图1所示,仅考虑耦合系统的二维平面模型,将卫星等航天器主体视为可绕其中心C转动的刚体,刚体中心是固定的,刚体半径为R。天线等柔性附属结构视为轴向运动的柔性梁结构,轴向速度为v(t)。其中,当v(t)>0表示柔性梁作轴向伸展运动;v(t)<0表示柔性梁作轴向收缩运动。航天器主体与柔性梁接口位于O点,柔性梁未伸出部分全部集中于接口处,其质量相对于航天器主体可忽略。建立两套坐标系,坐标系CX0Y0表示固定惯性坐标系;坐标系OXY以接口O为坐标原点,OX轴为柔性梁未变形的中性轴,该坐标系用于描述柔性梁的轴向运动和横向振动。OX轴和CX0轴的夹角用θ(t)表示,用于描述航天器主体的姿态扰动。
2 方程推导
如图1所示,航天器主体转动惯量用Ihub表示;均质柔性梁可看作是细长悬臂梁,线密度为ρ,轴向速度v(t)。柔性梁的外伸长度用L(t)表示,随时间发生变化,梁的初始外伸长度用L0表示。由于柔性梁作轴向运动,导致柔性梁横向产生振动,航天器主体产生姿态扰动,而柔性梁轴向运动、横向振动以及航天器主体姿态扰动三者之间是相互耦合的。
未变形前梁上任意一点的坐标为(x,0), 变形后该点坐标为(X(x,t),Y(x,t)), 航天器主体的扰动用θ(t)来表征。 假设OX轴和OY轴的单位矢量分别为i和j, 则柔性梁上任一点的位置矢量为:
r=(R+X)i+Y(X,i)j
(1)
式中:X=X(x,t),Y=(X,t)=Y(x,t)。
所以该点的绝对速度矢量为:
(2)
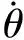
由上述一系列分析,可得耦合系统的动能为:
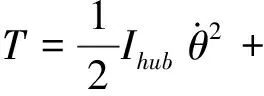
(3)
航天器在微重力场中运行,不考虑其重力势能,仅考虑其变形能,故耦合系统的势能为:
(4)

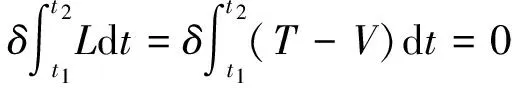
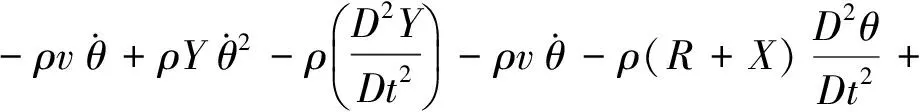
(5)
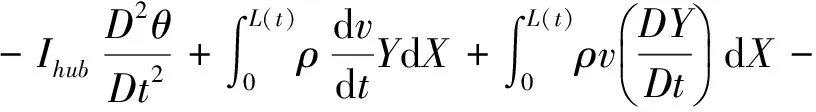
(6)
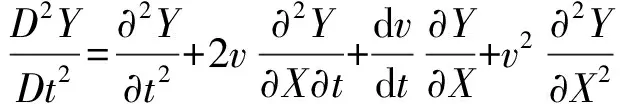
方程式(5)和式(6)是所研究系统精确模型的偏微分方程,根据小变形假设,忽略方程中高次项,可得系统一次刚柔耦合动力学模型的偏微分方程:
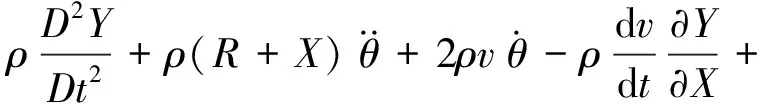
(7)
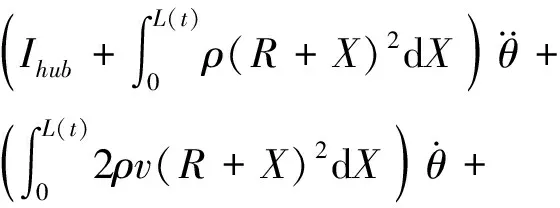
(8)
当不考虑刚-柔耦合作用时,可得到零次刚柔耦合动力学模型的偏微分方程:
(9)
当不考虑柔性梁轴向加速度,即梁的轴向速度是恒定不变的,此时可将方程式(7)~式(9)简化为:
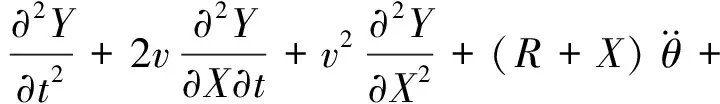
(10)
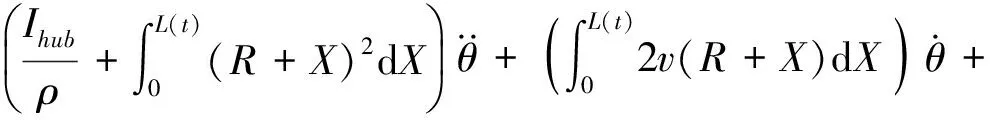
(11)
(12)
3 方程求解
3.1 假设模态法离散偏微分方程
推导出的耦合系统动力学方程是时变系数偏微分方程组,对于复杂的时变系数偏微分方程直接求解或采用积分的方法进行数值求解都是非常困难的。一般悬臂梁的振动偏微分方程可以采用假设模态法进行求解,得到用模态坐标表示的解耦方程,解出每一个模态坐标,根据振型叠加得到系统的总动力响应。但是,由于耦合系统中柔性梁的外伸长度随时间变化,柔性梁固有频率和固有振型已然失去了原有的物理意义。
本节采用修正的振型叠加法对方程式(10)~式(12)进行近似求解。根据分离变量和振型叠加法,可以把方程的解Y(X,t)假设为如下形式:
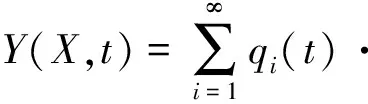
(13)
式中:φi(X,L)为柔性梁的瞬时模态, 它不仅与变量X有关, 而且与梁的外伸长度L(t)有关。
根据悬臂梁特征值理论, 可以把函数φi(X,L)写成如下形式:
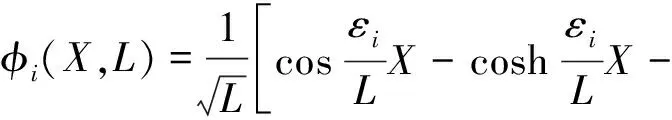
(14)
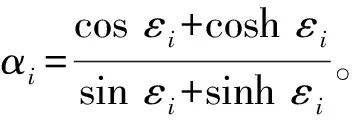

表1 特征值
将上述假设解代入偏微分方程式(10)~式(12)中,将得到含有假设模态形式的偏微分方程,根据振型函数的正交归一性质,可将所得的偏微分方程进一步整理化简为:
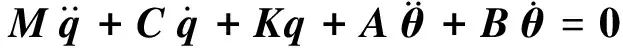
(15)
式中:
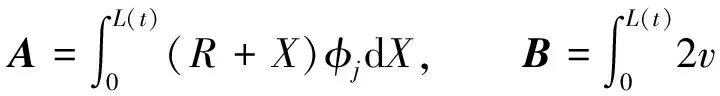
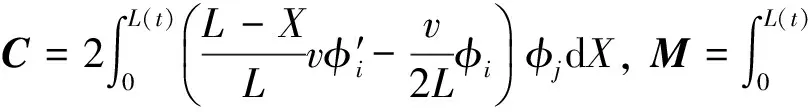
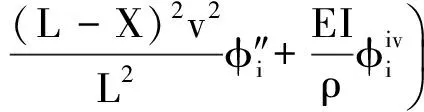
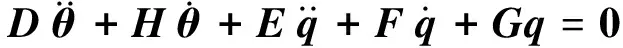
(16)
式中:
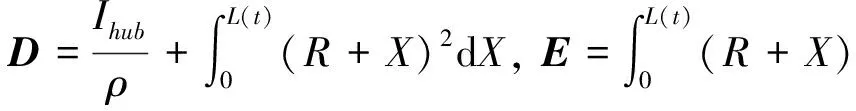
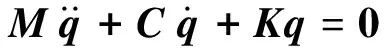
(17)
根据分块矩阵理论,将方程式(15)和式(16)合并成一个矩阵形式的偏微分方程组。即:
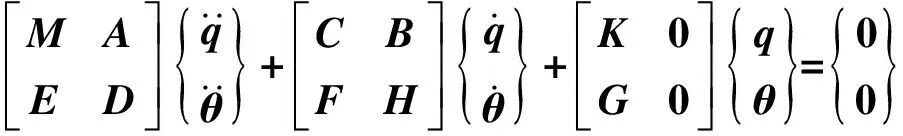
(18)
方程式(17)为不考虑刚柔耦合作用下的系统动力学方程,也是所研究模型的零次刚柔耦合动力学模型的偏微分方程。方程式(18)为航天器主体-轴向运动柔性梁刚-柔耦合系统的动力学方程,除时变系数外,与定常系统相比较,方程式(18)多出了伪阻尼项和几何刚度项,而且不仅存在惯性耦合,其刚度矩阵、阻尼矩阵均相互耦合。当不考虑弹性变形高阶项的影响时,利用数值方法对方程式(18)进行求解,最终可以得到柔性梁的横向位移和航天器主体的姿态角。
3.2 初始条件
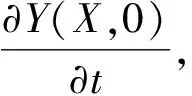
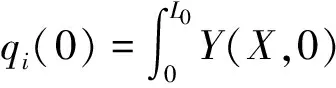
(19)
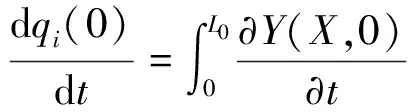
(20)
一般已知柔性梁的末端初始位移和初始速度,这里借助于材料力学中悬臂梁的挠曲方程,将柔性梁的末端初始位移和初始速度转化成柔性梁的初始位移和速度方程:
(21)
(22)
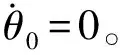
4 算例分析与讨论
系统总体动力学方程式(18)是用模态坐标表示的二阶时变系数偏微分方程。根据分析,取柔性梁前四阶振型进行数值计算,利用Matlab等数学软件,分别计算出各系数矩阵,采用四阶Runge-Kutta法对偏微分方程组进行数值求解。
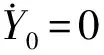
由于考虑了轴向运动柔性梁和航天器主体之间的刚-柔耦合作用,需要已知航天器主体半径R和转动惯量Ihub。对于圆柱形航天器主体而言,其转动惯量为:
(23)
式中:ρhub是航天器主体的密度;h是航天器主体的高度;R是航天器主体半径。
由于ρhub与h的乘积与R独立, 定义ρhub与h的乘积为航天器主体的面密度, 记作ρs=ρhubh。
根据文献[12]及航天器常识,航天器主体的物理参数拟采取R=0.1~5 m,ρs=100~15 000 kg/m2。
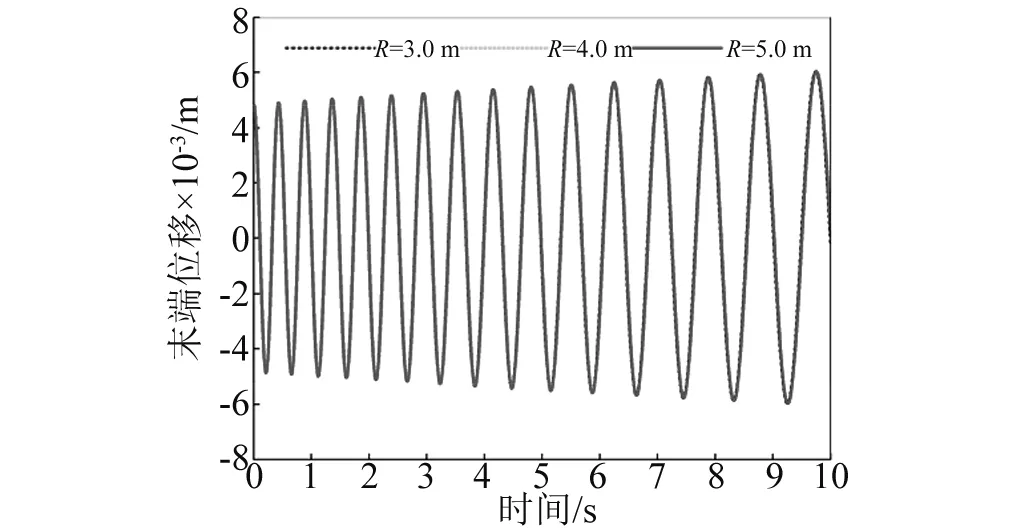
下面两图是航天器主体半径R=5 m和面密度ρs=15 000 kg/m2时柔性梁末端位移曲线。此时两者组合而成的航天器主体转动惯量最大。
如图2和图3所示,除增加航天器主体面密度和半径参数外,其余的物理参数与Park的研究完全相同,其数值模拟结果也完全一致。由此可以得出,在大转动惯量下,考虑刚柔耦合作用和不考虑刚柔耦合作用,柔性梁末端位移基本不变;这也从另一方面证明了建立的系统模型和推导出的动力学方程的正确性。
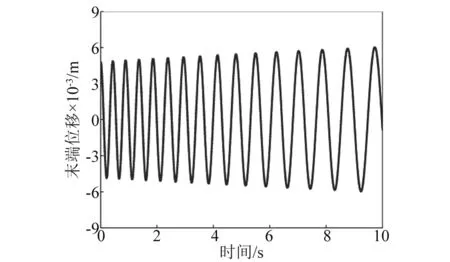
图2 大转动惯量下柔性伸展梁末端位移Fig.2 The tip displacement of the flexible beam in the large moment of inertia situation when deploying
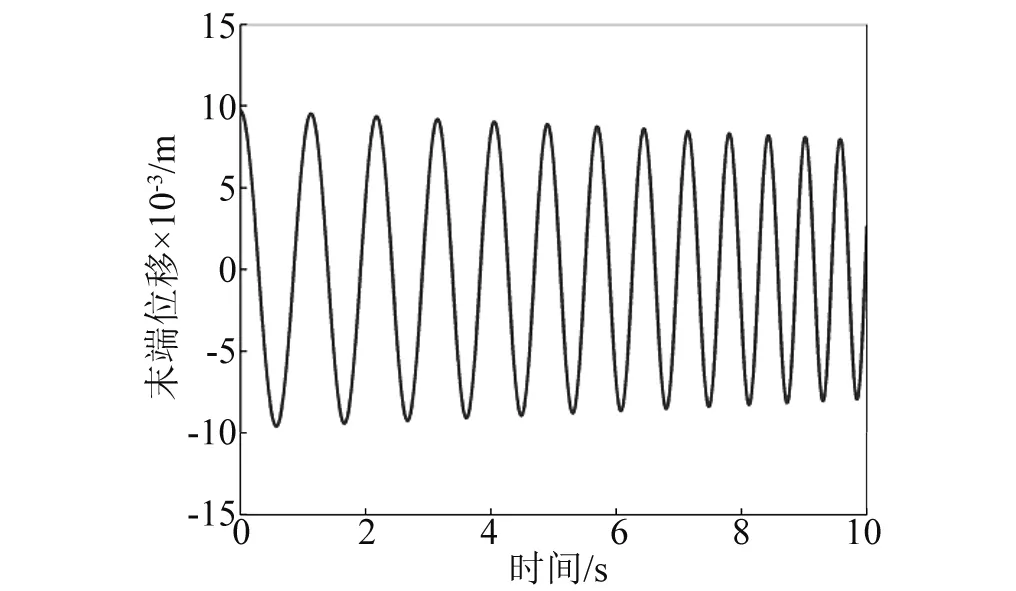
图3 大转动惯量下柔性收缩梁末端位移Fig.3 The tip displacement of the flexible beam in the large moment of inertia situation when retracting
需要指出的是,只要航天器主体的面密度和半径都取较大值,即航天器主体转动惯量取较大值时,其计算结果与Park的结论比较吻合。这是因为航天器主体的半径和面密度较大时,航天器主体相当于一个固定基础,类似于不考虑刚-柔耦合时,将航天器主体看作是固定基础。这也表明当航天器主体的转动惯量较大时,可以忽略柔性梁和航天器主体之间的刚-柔耦合作用。
4.1 航天器主体半径的影响
通过数值计算,在同一航天器主体面密度下,不同半径范围内的半径值对柔性梁末端位移以及对航天器姿态角的影响是不相同的。
在同一航天器主体面密度下,总是存在如下的规律:R[0.1,Rup1],柔性梁末端位移的振动随时间推移幅值有增有减;R[0.1,Rup2],航天器姿态角的振动随时间推移幅值也是有增有减。把柔性梁末端位移和航天器姿态角的振动随时间推移幅值有增有减的最大半径值称为无规律半径上限值,分别记作Rup1、Rup2。
R[Rdown,5],航天器主体半径值对柔性梁末端位移和航天器姿态角振动的影响非常小,可忽略不计。把对柔性梁末端位移和航天器姿态角的振动影响非常小的最小半径称为无影响半径下限值,记作Rdown。
[Rup1,Rdown]为柔性梁末端位移的振动随时间变化是有规律的半径区间, [Rup2,Rdown]为航天器姿态角的振动随时间变化是有规律的半径区间。在这两个有规律半径区间,柔性梁伸展时,随时间的推移,振动幅值逐渐增加;柔性梁收缩时,随时间的推移,振动幅值逐渐减小。
将Rup1、Rup2和Rdown统称为半径临界值,每一个航天器主体面密度都对应着相应的三个半径临界值。此外,每个半径临界值都对应着一个相应的转动惯量,把半径临界值对应的转动惯量值作如下定义:
定义Rup1对应的转动惯量Iup1为航天器在同一面密度下使柔性梁末端位移幅值随时间变化有增有减的最大转动惯量;
定义Rup2对应的转动惯量Iup2为航天器在同一面密度下使航天器姿态角幅值随时间变化有增有减的最大转动惯量;
定义Rdown对应的转动惯量Idown为航天器在同一面密度下对柔性梁位移和航天器姿态角影响较小的最小转动惯量。
三个临界转动惯量Iup1、Iup2、Idown的表达式如下所示,它们的物理意义是三个临界半径值对应的航天器主体转动惯量值。
(24)
(25)
(26)
为确定各个面密度对应的半径临界值Rup1、Rup2和Rdown,作如下规定:
当航天器半径R大于某一值后,柔性梁末端位移的幅值总是按升降规律排列,此时的半径值为Rup1;
当航天器半径R大于某一值后,航天器姿态角的幅值总是按升降规律排列,此时的半径值为Rup2;
当航天器半径R大于某一值后,柔性梁末端位移的各个幅值与此面密度下R=5 m时末端位移的对应幅值之差的绝对值总小于一个很小的常数,此时的半径值为Rdown。本文中对应幅值之差的绝对值取10-5m。
换言之,就是利用数值方法计算出同一面密度下的所有半径对应的柔性梁末端位移和航天器姿态角,按上述规定分别计算出各个面密度对应的Rup1、Rup2和Rdown。下面计算柔性梁伸展时不同航天器主体面密度下的半径临界值,航天器主体面密度分别取100 kg/m2、500 kg/m2、1 000 kg/m2、2 000 kg/m2、4 000 kg/m2、6 000 kg/m2、8 000 kg/m2、10 000 kg/m2、15 000 kg/m2,计算结果如表2所示。

表2 伸展时半径临界值
对伸展时航天器主体半径临界值进行拟合,将得到很好的拟合公式:
(27)
其中:SSE=6.037×10-6R21
(28)
其中:SSE=2.376×10-5R20.999 9
(29)
其中:SSE=3.589×10-5R21
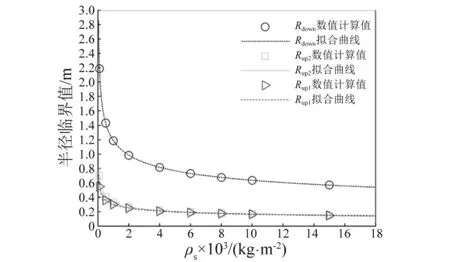
图4 伸展时临界半径值拟合曲线Fig.4 The fitting curve of critical radius when deploying
拟合式(27)~式(29)能够很好地预测柔性梁伸展时不同航天器主体面密度下半径临界值。
例如,当ρs=5 000 kg/m2时,拟合公式预测结果为:Rup1=0.197 3、Rup2=0.206 2、Rdown=0.768 9;数值计算结果为:Rup1=0.196 5、Rup2=0.207 8、Rdown=0.767 3。公式预测结果和数值计算结果非常接近。
同理,计算柔性梁收缩时不同航天器主体面密度下的半径临界值和转动惯量临界值,结果如表3所示。
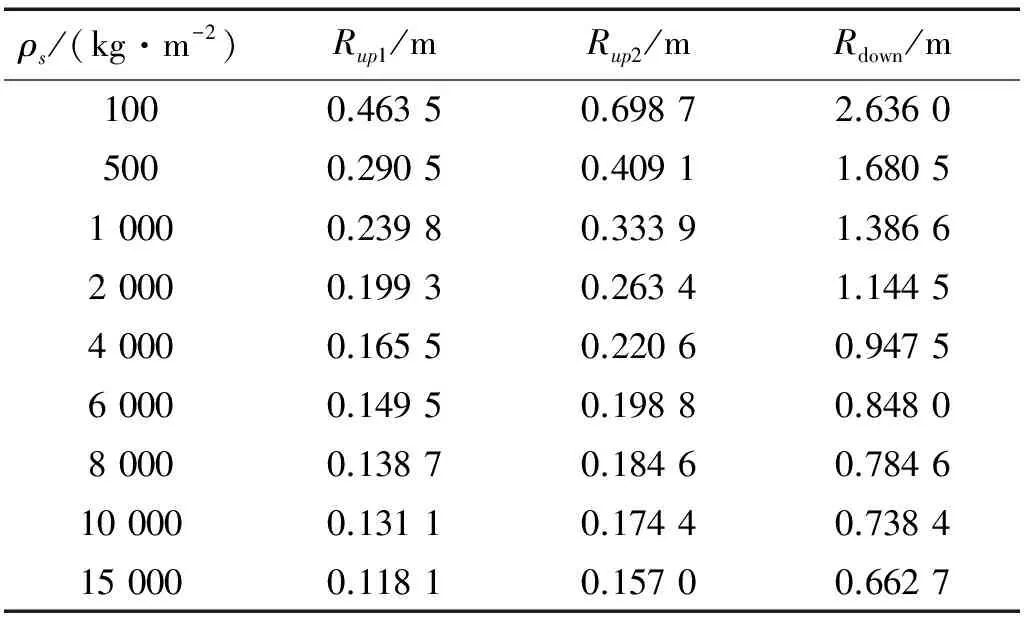
表3 收缩时半径临界值
对收缩时航天器主体半径临界值进行拟合,也将得到很好的拟合公式:
(30)
其中:SSE=1.831×10-6R21
(31)
其中:SSE=4.184×10-5R20.999 8
(32)
其中:SSE=7.021×10-7R21
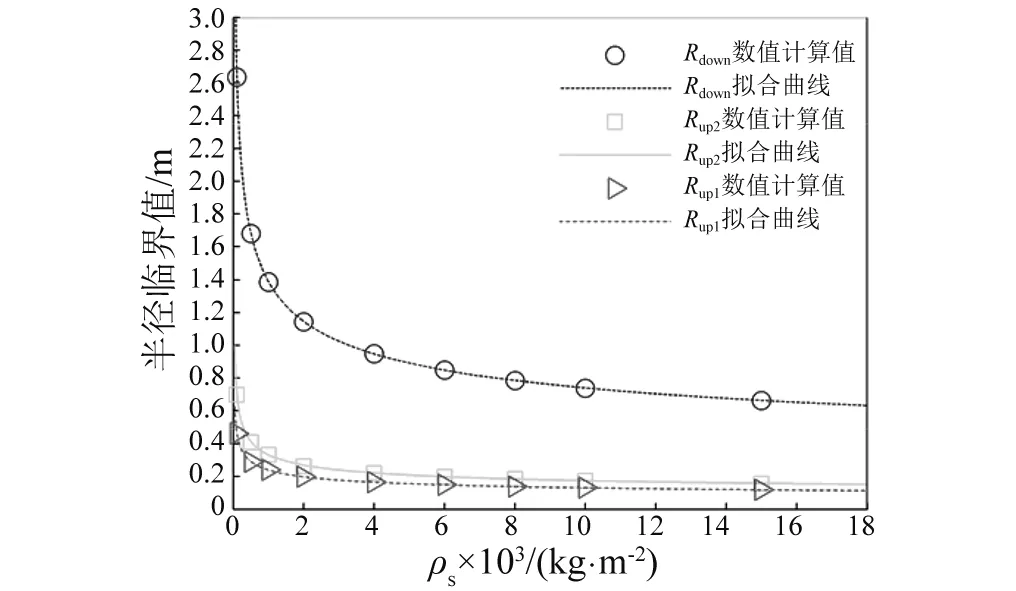
图5 收缩时临界半径值拟合曲线Fig.5 The fitting curve of critical radius when retracting
拟合式(30)~式(32)能够很好地预测柔性梁收缩时不同航天器主体面密度下半径临界值。
例如,当ρs=3 000 kg/m2时,拟合公式预测结果为:Rup1=0.178 3、Rup2=0.238 8、Rdown=1.024 8,数值计算结果为:Rup1=0.178 5、Rup2=0.237 4、Rdown=1.024 5。
当ρs=5 000 kg/m2时,拟合公式预测结果为:Rup1=0.156 1、Rup2=0.207 7、Rdown=0.891 5;数值计算结果为:Rup1=0.156 5、Rup2=0.208 3、Rdown=0.891 8。公式预测结果和数值计算结果非常接近。
由上述几个拟合公式可以预测出在某一航天器主体面密度下的三个半径临界值,从而了解在该面密度下半径对耦合系统动力响应的影响区间。
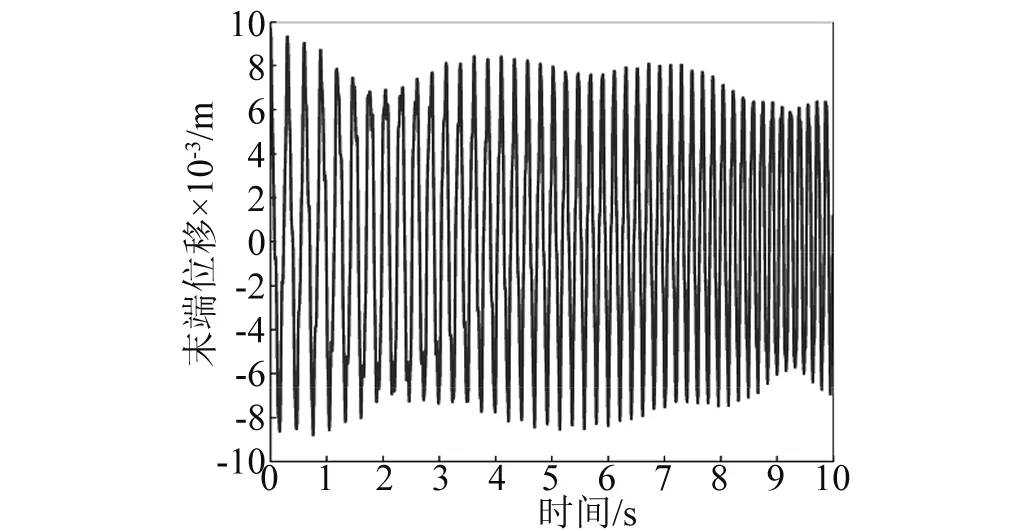
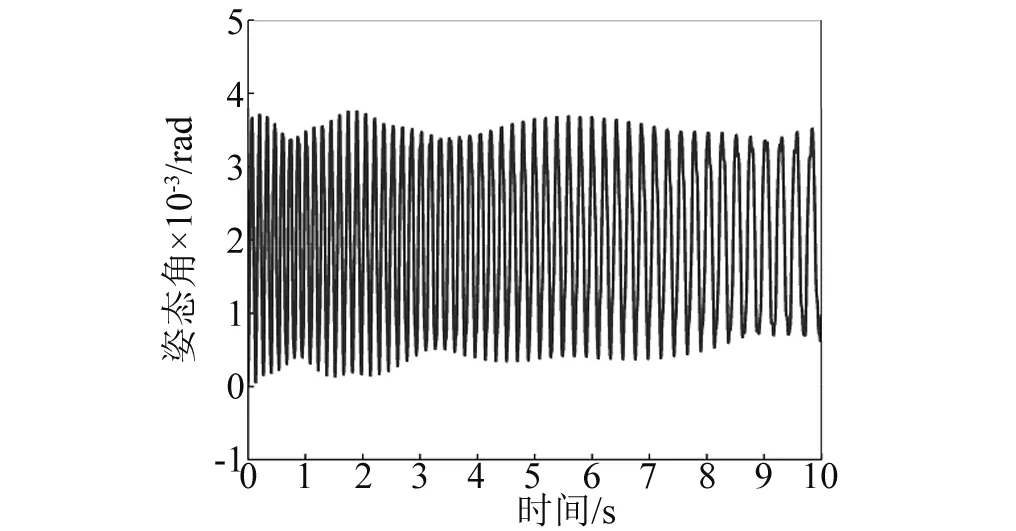
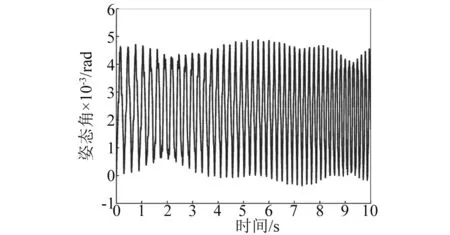
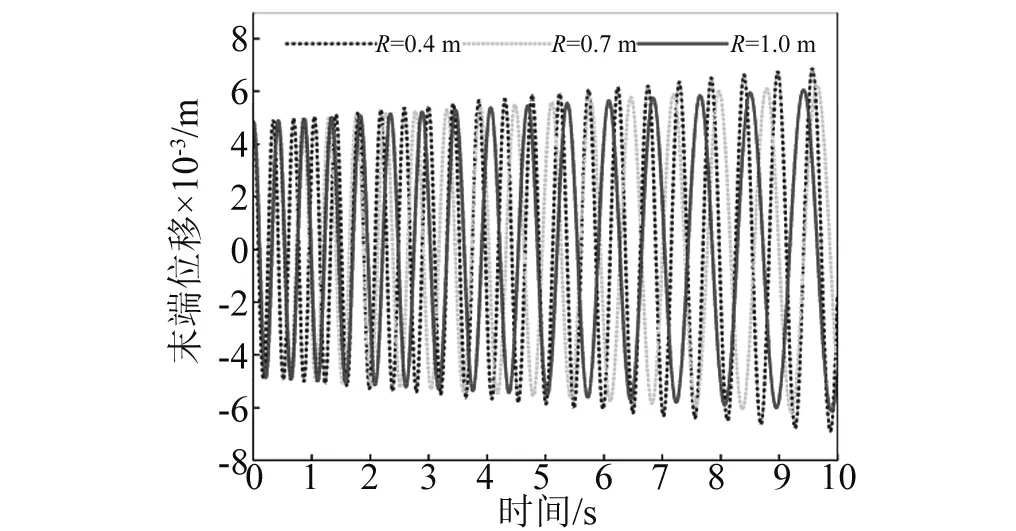
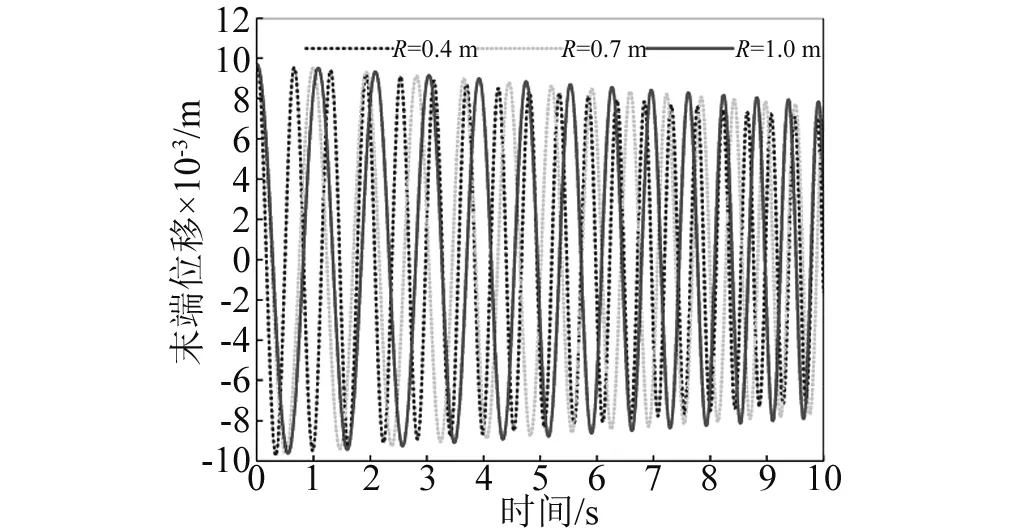
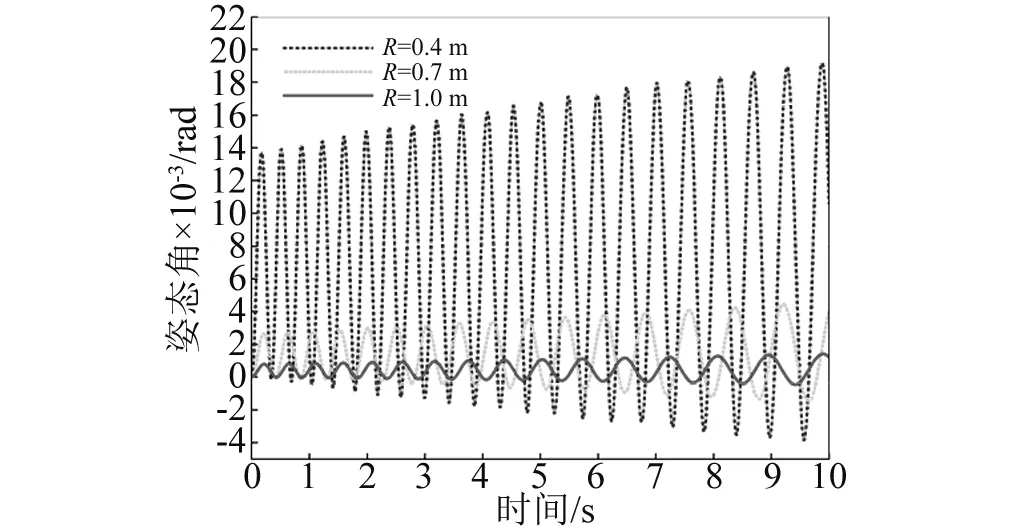
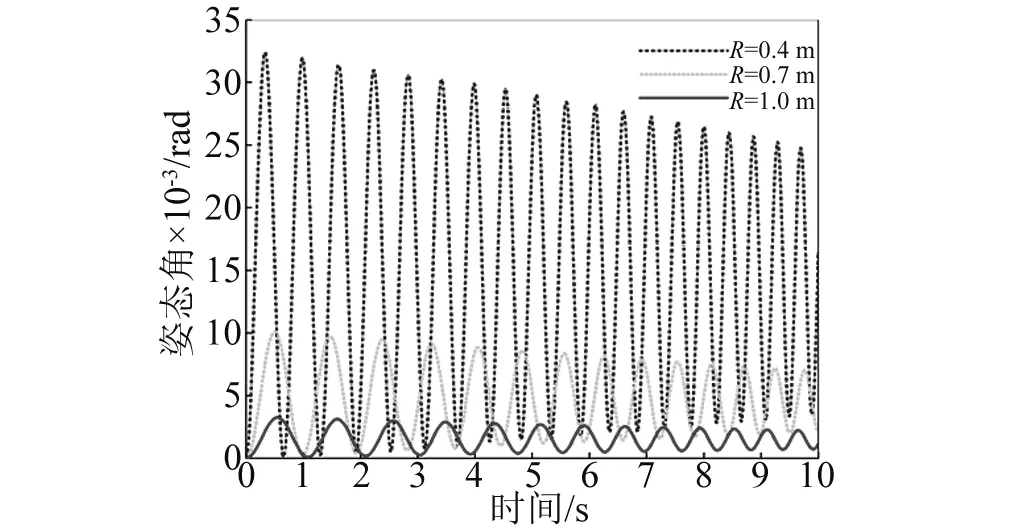
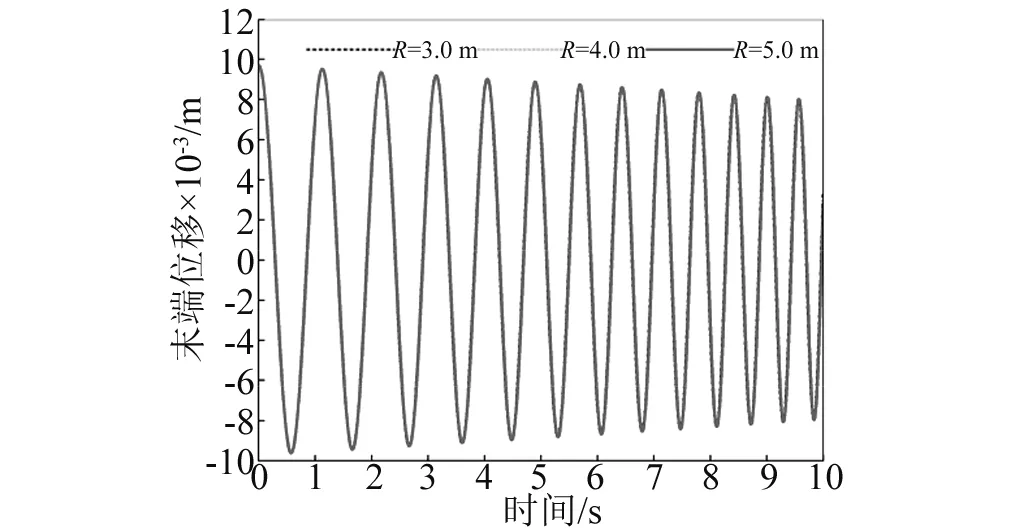
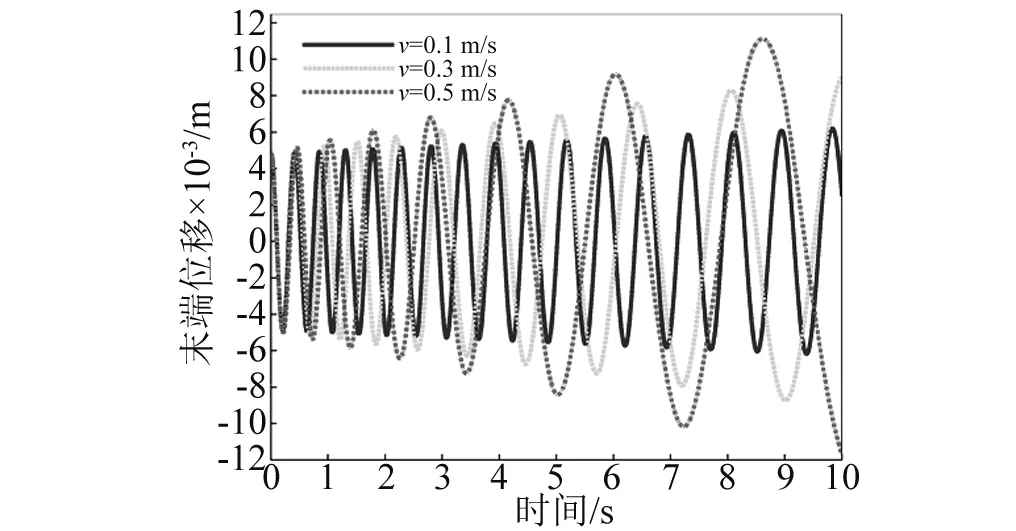
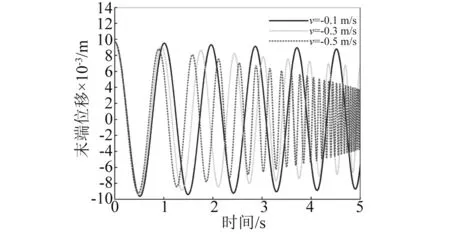
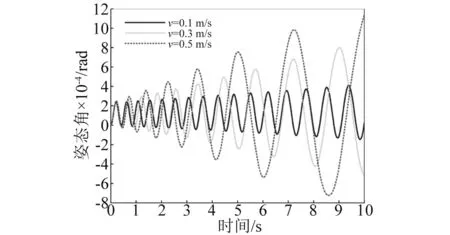
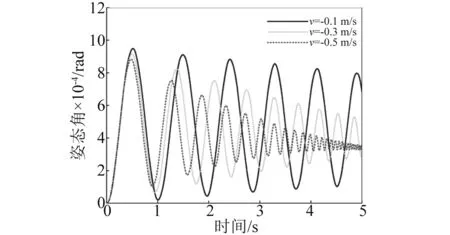
数值计算还发现:不管柔性梁是伸展还是收缩,同一航天器面密度下,柔性梁末端位移振动无规律半径上限值总小于航天器姿态角振动无规律半径上限值,即Rup1 其次,随着航天器主体面密度的增加,Rup1、Rup2和Rdown的值逐渐减小,对应的临界转动惯量值Iup1、Iup2、Idown也在逐渐减小。 根据柔性梁伸展或收缩时的半径临界值Rup,航天器主体半径和面密度分别取R=0.2 m,ρs=500 kg/m2,进行数值计算。此时半径值R小于该面密度下半径临界值Rup,数值计算结果反应的是无规律半径区间柔性梁末端位移和航天器姿态角的振动特性。 需要指出的是,在同一面密度下,不管伸展还是收缩情形,只要航天器主体半径值取小于Rup,得到的柔性梁末端位移和航天器姿态角的振动规律和不考虑刚柔耦合时的振动规律不同。不考虑刚柔耦合作用,柔性梁伸展时,柔性梁末端做幅值递增,振动频率减小的振动;柔性梁收缩时,柔性梁末端做幅值递减,振动频率增大的振动。 图6~图9分别是航天器主体半径在无规律半径区间取值时,柔性梁末端位移和航天器姿态角曲线图。这四图表明:当航天器主体半径处于无规律半径区间时,柔性梁的末端位移和航天器姿态角随时间推移,其幅值有增有减。需要指出的是,R越接近于Rup,其幅值波动越不明显,并逐渐趋向于递增或递减。 图6 伸展时无规律半径下柔性梁末端位移Fig.6 The tip displacement of the flexible beam in the irregular radius situation when deploying 图7 收缩时无规律半径下柔性梁末端位移Fig.7 The tip displacement of the flexible beam in the irregular radius situation when retracting 图8 伸展时无规律半径下航天器姿态角Fig.8 The attitude angle of the spacecraft in the irregular radius situation when deploying 图9 收缩时无规律半径下航天器姿态角Fig.9 The attitude angle of the spacecraft in the irregular radius situation when retracting 在有影响半径区间[Rup,Rdown]取不同的半径进行数值计算,分析有影响区间的不同半径对柔性梁末端位移和航天器姿态角的影响。 利用控制变量法,使航天器主体面密度、柔性梁轴向速度和初始条件分别采用相同值,而航天器主体半径在[Rup,Rdown]区间取不同半径值。航天器主体面密度拟采取ρs=500 kg/m2,航天器主体半径拟采取0.4 m、0.7 m、1.0 m。分别计算这三个不同半径下的柔性梁末端位移和航天器姿态角,再将三个不同半径下的动力响应进行对比。 图10和图11分别是在有影响区间取不同的半径值时,柔性伸展(收缩)梁末端位移曲线图。可以看出,在该半径区间内,对于同一半径下,随时间的推移,柔性伸展(收缩)梁末端位移幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同半径下,随着半径的增加,柔性伸展(收缩)梁末端位移幅值在逐渐减小(增大),周期在增加,频率在下降。 图12和图13分别是在有影响区间取不同的半径值,航天器在伸展(收缩)时的姿态角曲线图。可以看出,在该半径区间内,对于同一半径下,柔性梁在伸展(收缩)时,随时间的推移,航天器姿态角幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同半径下,柔性梁在伸展(收缩)时,随着半径的增加,航天器姿态角幅值在减小,周期在增加,频率在降低。 图10 伸展时有影响半径区间不同半径下柔性梁末端位移Fig.10 The tip displacement of the flexible beam at the different radius located in the influence interval when deploying 图11 收缩时有影响半径区间不同半径下柔性梁末端位移Fig.11 The tip displacement of the flexible beam at the different radius located in the influence interval when retracting 图12 伸展时有影响半径区间不同半径下航天器姿态角Fig.12 The attitude angle of the spacecraft at the different radius located in the influence interval when deploying 图13 收缩时有影响半径区间不同半径下航天器姿态角Fig.13 The attitude angle of the spacecraft at the different radius located in the influence interval when retracting 换言之,在区间[Rup,Rdown]内的半径对航天器姿态角和柔性梁末端位移是有影响的,在该半径区间内不可以忽略轴向运动柔性梁和航天器主体之间的刚-柔耦合作用。研究此类系统动力学响应时,应该考虑轴向运动柔性梁和航天器主体之间的刚-柔耦合作用。 最后在无影响半径区间[Rdown,5]取不同的半径进行数值计算,分析无影响区间的不同半径对柔性梁末端位移和航天器姿态角的影响。 图14和图15分别是在无影响半径区间取不同的半径值时,柔性伸展(收缩)梁末端位移曲线图。可以看出,在该半径区间内,对于同一半径下,随时间的推移,柔性伸展(收缩)梁末端位移幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同半径下,三个半径对应的柔性伸展(收缩)梁末端位移曲线重合。即在该半径区间,航天器主体半径的变化对柔性梁末端位移的影响很小。 图14 伸展时无影响半径区间不同半径下柔性梁末端位移Fig.14 The tip displacement of the flexible beam at the different radius located in the no influence interval when deploying 图15 收缩时无影响半径区间不同半径下柔性梁末端位移Fig.15 The tip displacement of the flexible beam at the different radius located in the no influence interval when retracting 图16和图17分别是在无影响半径区间取不同的半径值,航天器在柔性梁伸展(收缩)时的姿态角曲线图。可以看出,在该半径区间内,对于同一半径下,柔性梁在伸展(收缩)时,随时间的推移,航天器姿态角幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同半径下,柔性梁在伸展(收缩)时,随着半径的增加,航天器姿态角幅值减小,周期基本不变。但在该半径区间,航天器姿态角幅值的量级非常小,也可以直接忽略不计。 图16 伸展时无影响半径区间不同半径下航天器姿态角Fig.16 The attitude angle of the spacecraft at the different radius located in the no influence interval when deploying 图17 收缩时无影响半径区间不同半径下航天器姿态角Fig.17 The attitude angle of the spacecraft at the different radius located in the no influence interval when retracting 换言之,在无影响半径区间的半径值对航天器姿态角和柔性梁末端位移没有影响,为简化计算,航天器主体半径在无影响半径区间时,可以不考虑轴向运动柔性梁和航天器主体之间的刚-柔耦合作用。 在区间[0.1,Rup]取同一半径值,对应的各个面密度下的柔性梁末端位移和航天器姿态角随时间变化幅值有增有减,研究航天器主体面密度对柔性梁末端位移和航天器姿态角的影响没有意义。 在区间[Rup,5]取同一半径值,航天器主体面密度的变化对柔性梁末端位移和航天器姿态角的影响可忽略不计。 在不同面密度对应的有影响半径区间取同一半径值,面密度拟采取1 000 kg/m2、2 000 kg/m2、4 000 kg/m2,航天器主体半径拟采取R=0.4 m。 图18和图19分别是不同航天器主体面密度下柔性伸展(收缩)梁的末端位移曲线图。在半径区间[Rup,Rdown]取同一半径值时,对于同一面密度下,随时间的推移,柔性伸展(收缩)梁的末端位移幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同面密度下,随航天器主体面密度的增加,柔性梁的末端位移的幅值在逐渐减小(增加),周期都在增长,频率都在降低。 图18 伸展时在不同面密度下柔性梁末端位移Fig.18 The tip displacement of the flexible beam at different surface densities when deploying 图19 收缩时在不同面密度下柔性梁末端位移Fig.19 The tip displacement of the flexible beam at different surface densities when retracting 图20和图21分别是不同航天器主体面密度下航天器在柔性梁伸展(收缩)时的姿态角曲线图。在半径区间[Rup,Rdown]取同一半径值时,对于同一面密度下,柔性梁伸展(收缩)时,随时间的推移,航天器姿态角幅值在逐渐增加(减少),周期逐渐增长(缩短),频率逐渐降低(上升);对于不同面密度下,随航天器主体面密度的增加,航天器姿态角的幅值都在减小,周期都在增长,频率都在降低。 图20 伸展时不同面密度下航天器姿态角Fig.20 The attitude angle of the spacecraft at different surface densities when deploying 图21 收缩时不同面密度下航天器姿态角Fig.21 The attitude angle of the spacecraft at different surface densities when retracting 换言之,半径在区间[Rup,Rdown]内取值,航天器的主体面密度对航天器姿态角和柔性梁末端位移是有影响,这种影响来源于柔性梁和航天器主体之间的刚-柔耦合作用,而且影响规律和有影响半径区间内的不同半径对柔性梁末端位移和航天器姿态角的影响相似。 数值计算航天器主体的面密度和主体半径分别采用相同值时,柔性梁轴向伸展(收缩)速度对柔性的末端位移以及对航天器姿态角的影响。 图22和图23分别为柔性梁在不同的伸展(收缩)速度下的末端位移曲线图。可以看出,对于同一轴向速度下,随着时间的推移,柔性梁末端位移振动的幅值逐渐增加(降低),振动周期逐渐增长(减短),振动频率逐渐下降(上升)。这是由于随着时间推移,柔性梁外伸部分越来越长(短),柔性梁的刚度变得越来越小(大),所以导致柔性梁末端位移增加(降低)。在不同伸展(收缩)速度下,伸展(收缩)速度越大,随着时间的推移,柔性梁末端位移的振动幅值增加(减少)得越快,而且轴向速度越大,其平均振动周期越大(小),振动频率越小(大),这是由于伸展(收缩)速度越大,相同时间内柔性梁外伸部分越长(短),相应柔性梁的刚度变得更小(大),从而导致柔性的末端位移幅值越大(小)。 图24和图25分别为航天器主体半径为R=0.5 m,面密度为ρs=2 000 kg/m2时,航天器在不同的伸展(收缩)速度下的姿态角响应图。可以看出,对于同一伸展(收缩)速度下,随着时间的推移,姿态角的振幅逐渐增加(或降低),振动周期逐渐增长(缩短),振动频率逐渐下降(上升)。在不同伸展速度下,伸展(收缩)速度越大,随着伸展时间的推移,航天器姿态角的振幅增加(减少)得越快,振动周期增加(减少)得越长,振动频率下降(上升)越快。 图22 在不同伸展速度下柔性梁末端位移Fig.22 The tip displacement of the flexible beam at different deploying velocities 图23 在不同收缩速度下柔性梁末端位移Fig.23 The tip displacement of the flexible beam at different retracting velocities 图24 在不同伸展速度下航天器姿态角Fig.24 The attitude angle of the spacecraft at different deploying velocities 图25 在不同伸展速度下航天器姿态角Fig.25 The attitude angle of the spacecraft at different retracting velocities 需要指出的是,在本文研究的航天器主体面密度和半径范围内,面密度和半径取不同的组合值,轴向速度对航天器姿态角影响规律和上述规律是一致的,但是在大转动惯量下,不同伸展(收缩)速度下的航天器姿态角都特别小。在航天器姿态控制精度范围内,完全可以忽略柔性梁轴向速度对航天器姿态的影响。即在航天器主体转动惯量较大时,柔性梁轴向运动引起的航天器姿态扰动可忽略不计,只需要考虑柔性梁轴向运动引起的横向位移,而无需考虑航天器姿态角与柔性梁轴向运动和横向振动的耦合作用。 本文利用Hamilton原理推导出航天器主体和轴向运动柔性梁刚-柔耦合系统的动力学方程。考虑了柔性梁轴向运动与柔性梁横向振动以及航天器姿态角振动的相互耦合作用,利用分离变量法和假设模态法求解系统动力学方程,采用四阶Runge-Kutta法和Matlab软件进行数值计算。数值计算中考虑了航天器主体半径、航天器主体面密度和柔性梁轴向速度对柔性梁横向振动和对航天器姿态角的影响。 数值计算表明,不同半径范围内的航天器主体半径值对柔性的末端位移以及对航天器姿态角的影响是不相同的。 航天器主体半径小于无规律半径上限值时,随时间变化,柔性梁末端位移和航天器姿态角做幅值有增有减的振动; 航天器主体半径处于有规律半径区间时,随时间变化,柔性梁伸展时,柔性梁末端位移和航天器姿态角做幅值递增振动,振动频率逐渐降低;柔性梁收缩时,柔性梁末端位移和航天器姿态角做幅值递减振动,振动频率逐渐升高; 航天器主体半径大于无影响半径下限值时,可以不考虑航天器主体和轴向运动柔性梁之间的刚-柔耦合作用。 其次,不管柔性梁是伸展还是收缩,随着航天器主体面密度的增加,航天器主体半径的三个临界值在逐渐减小,对应的临界转动惯量值也在逐渐减小。 其中航天器主体半径处于有规律半径区间时,航天器主体半径和航天器主体面密度对柔性梁末端位移和航天器姿态角的影响规律是相同的。柔性梁伸展时,随航天器主体半径或面密度的增加,柔性梁末端位移幅值在减小,周期在增长,频率在降低;柔性梁收缩时,随航天器主体半径或面密度的增加,柔性梁末端位移幅值在增加,周期在增长,频率在降低;不管柔性梁伸展还是收缩,随航天器主体半径或面密度的增加,航天器姿态角幅值都在减小,周期都在增长,频率都在下降;柔性梁轴向速度对柔性梁末端位移和航天器姿态角的影响规律是一致的。柔性梁伸展时,轴向伸展速度越大,柔性梁末端位移幅值和航天器姿态角幅值越大,周期越长,频率越低;反之,柔性梁收缩时,轴向收缩速度越大,柔性梁末端位移幅值和航天器姿态角幅值越小,周期越小,频率越高。 [ 1 ] TABARROK B, LEECH C M, KIM Y I. On the dynamics of an axially moving beam [J]. Journal of the Franklin Institute, 1974, 297(3): 201-220. [ 2 ] 沈少萍,李智斌. 末端带集中质量的可伸展挠性附件与航天器姿态耦合动力学分析[J]. 振动与冲击,2008, 27(5): 115-118. SHEN Shaoping, LI Zhibin. Attitude dynamics of a spacecraft with tip mass attached deploying flexible appendage [J]. Journal of Vibration and Shock, 2008, 27(5): 115-118. [ 3 ] WANG L H, HU Z D, ZHONG Z, et al. Hamiltonian dynamic analysis of an axially translating beam featuring time-variant velocity [J]. Acta Mech, 2009, 178(4): 149-161. [ 4 ] 刘宁,杨国来. 移动质量作用下轴向运动悬臂梁振动特性分析[J]. 振动与冲击,2012,31(3): 102-105. LIU Ning, YANG Guolai. Vibration property analysis of axially moving cantilever bean considering the effect of moving mass [J]. Journal of Vibration and Shock, 2012,31(3): 102-105. [ 5 ] PARK S, YOO H H, CHUNG J T. Vibrations of an axially moving beam with deployment or retraction [J]. AIAA Journal, 2013, 51(3): 686-696. [ 6 ] SHEN Z X, TIAN Q, LIU X N. Thermally induced vibrations of flexible beams using Absolute Nodal Coordinate Formulation [J]. Aerospace Science and Technology, 2013, 29(1): 386-393. [ 7 ] YANG X D, ZHANG W. Nonlinear dynamics of axially moving beam with coupled longitudinal-transversal vibrations [J]. Nonlinear Dynamics, 2014, 78(4): 2547-2556. [ 8 ] 陈红永,陈海波,张培强. 轴向受压运动梁横向振动特性的数值分析[J]. 振动与冲击,2014, 33(24): 101-105. CHEN Hongyong, CHEN Haibo, ZHANG Peiqiang. Numerical analysis of free vibration of an axially moving beam under compressive load [J]. Journal of Vibration and Shock, 2014, 33(24): 101-105. [ 9 ] 闫业毫,和兴锁,邓峰岩. 空间柔性梁的刚-柔耦合动力学特性分析与仿真[J]. 西北工业大学学报,2016,34(3): 480-484. YAN Yehao, HE Xingsuo, DENG Fengyan. Analyzing and imitation of dynamic properties for rigid-flexible coupling systems of a spatial flexible beam [J]. Northwestern Polytechnical University, 2016, 34(3): 480-484. [10] 孙述鹏,王伟,段枭. 航天器刚柔耦合动力学建模及热诱发动力学响应分析[J]. 振动与冲击, 2016, 35(24): 79-83. SUN Shupeng, WANG Wei, DUAN Xiao. Rigid-flexiblecoupling dynamic modelling and thermally induced vibration analysis for a flexible spacecraft [J]. Journal of Vibration and Shock, 2016, 35(24): 79-83. [11] 洪嘉振,刘铸永. 刚柔耦合动力学的建模方法[J]. 上海交通大学学报(自然版), 2008, 42(11): 1922-1926. HONG Jiazhen, LIU Zhuyong. Modeling methods of rigid-flexible coupling dynamics [J]. Journal of Shanghai Jiaotong University(Sci.), 2008, 42(11): 1922-1926. [12] 董彦芝,刘芃,王国栋,等. 航天器结构用材料应用现状与未来需求[J]. 航天器环境工程, 2010, 27(1): 41-44. DONG Yanzhi, LIU Peng, WANG Guodong et al. Application and future demand of materials for spacecraft structures [J]. Spacecraft Environment Engineering, 2010, 27(1): 41-44.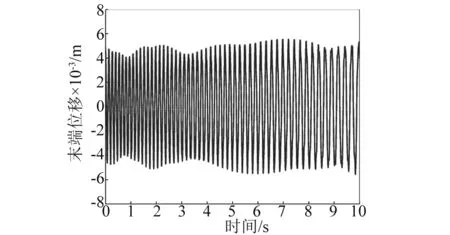
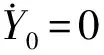
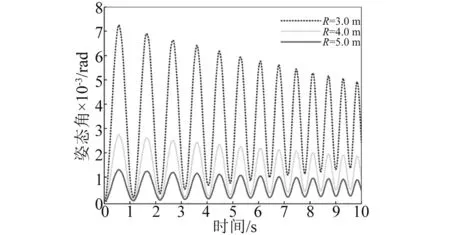
4.2 航天器主体面密度的影响
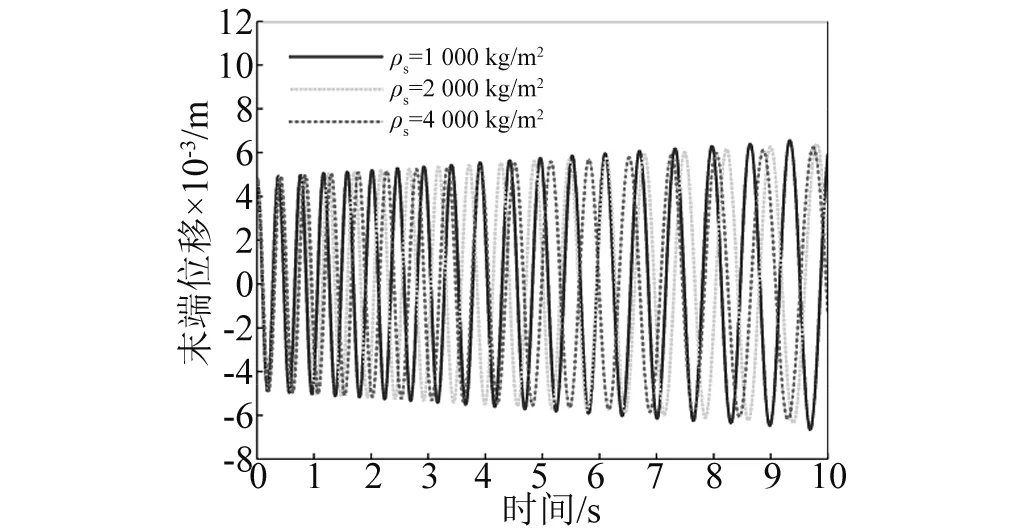
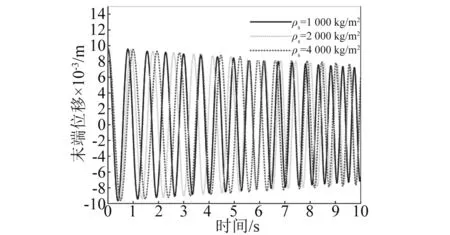
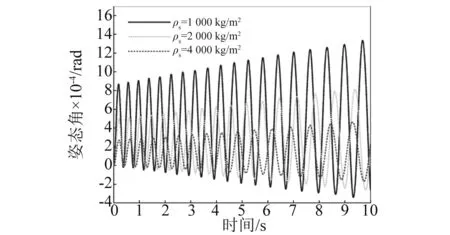
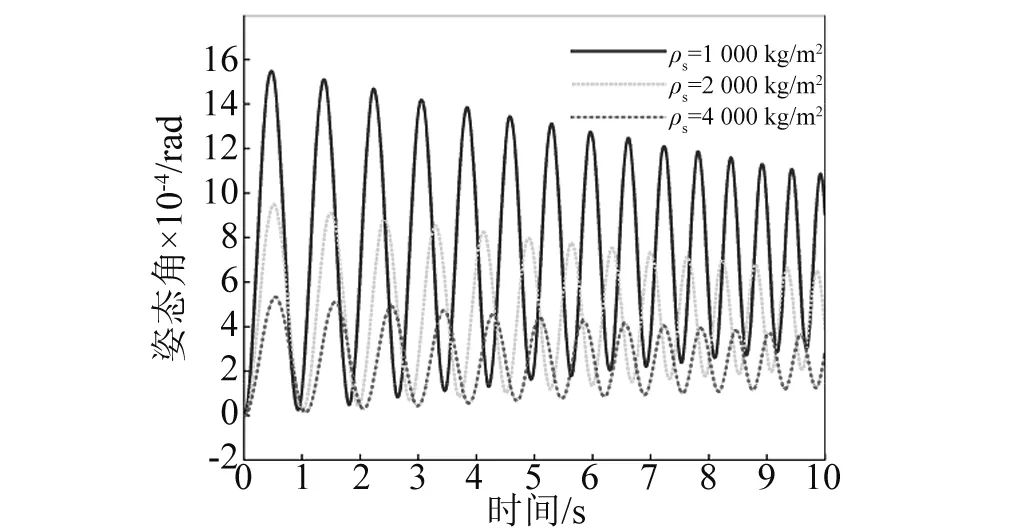
4.3 轴向速度的影响
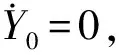
5 结 论

