多目标下桥梁上部结构更换方法模糊决策研究*

陈金州 吴大健 夏 飞

(中交第二公路勘察设计研究院有限公司 武汉 430056)

由于新旧设计标准的差异、结构材料风化、运输量快速增长，以及重载车辆虐行等原因，桥梁工程结构物老化与性能退化的现象日益突出，使得整体结构将陆续达到设计使用寿命[1]。当其安全性、可靠性，以及交通通行能力和适应城市规划发展等功能难以满足交通需求时，桥梁结构就可能面临着拆除与重建。

为了获得一个满意的桥梁上部结构快速更换施工方案，往往在收集和整理评估所需资料时，偏重有利于被选择的施工方案有关信息与资料，所有资料都成为了方案“科学”的有力论据；同时，论证时，个人的经验和观点等也具备一定的主观臆断和片面性及随机性[2]。

但是，施工方案是由相互交叉关联、相互渗透制约， 以及相互依存发展的众多因素构成的复杂且缺少定量数据的系统决策，如何将这种模糊性指标加以定量化，使因素评估和评估结果建立在科学基础之上，就需要应用模糊数学方法[3]，进行决策优选研究。

1 决策模型的建立

1.1 层次结构模型

方案优选的目的是获取安全可靠、技术可行、快速便民、经济合理，以及工期可控的最佳施工方案。其过程体现为：在充分了解桥梁上部结构的基础上，从“人、机、物、料、法、环”出发，结合安全、技术，以及工期等多维度，筛选影响更换方案(拆除和新建方案)选择的多重因素，组建评估因素集。依据不同的桥梁上构、不同的要求构建适当的评价层次等级和因素集，将它们划分为多个评判层次和指标体系；对众多备选方案形成评价结果集，从中选出一个满足实际需求的最佳施工方案。其层次结构见图1[4]，本文案例有3个备选方案，因此层次结构图的方案层包含3个备选方案。

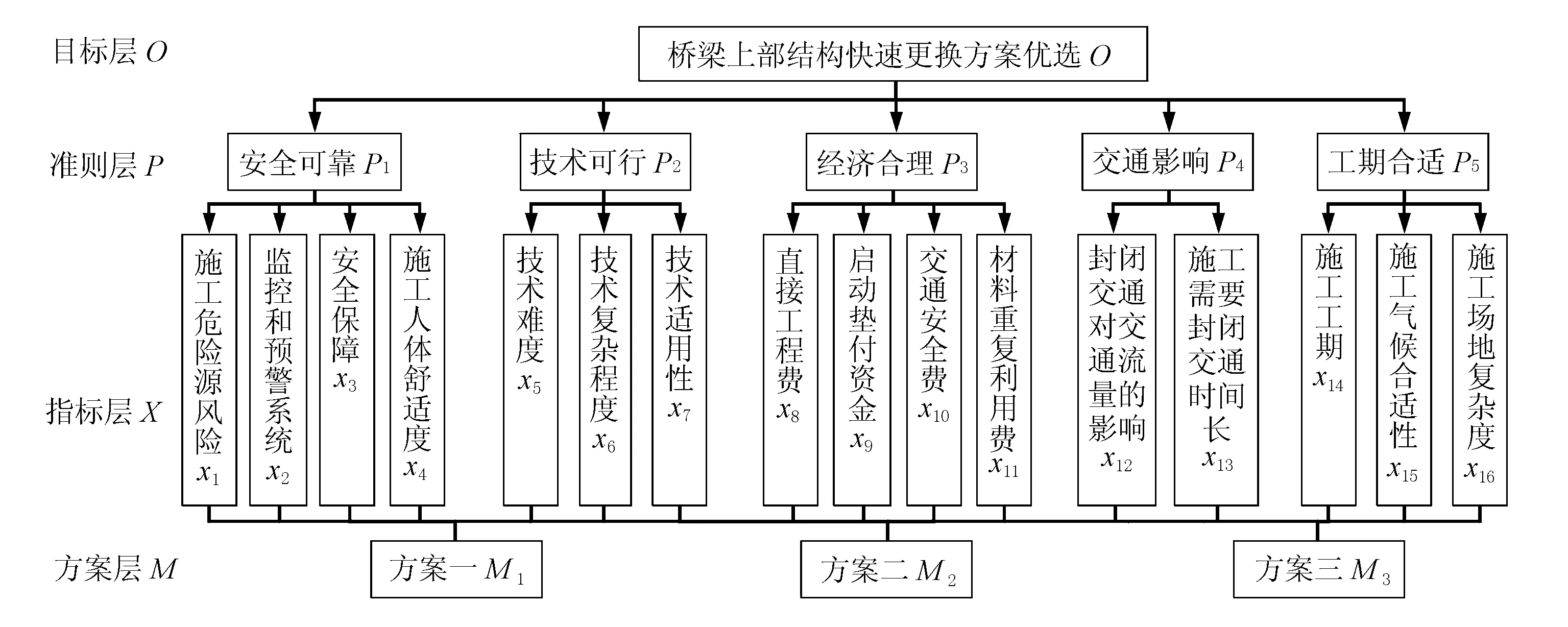
图1 桥梁上部结构快速更换方案优选层次结构图

1.1.1确定备选方案集

桥梁快速更换包括快速拆除和快速安装。在桥梁上部结构拆除方面，可以分为三大类：①分块分段切割拆除；②分单元或整体移除；③现场破碎拆除。在桥梁安装方面，也可以划分为两大类：①分单元预制安装；②整体预制移运；③现场浇注。

1.1.2确定各层级评价因素的权重

针对桥梁快速更换技术评价，国内外均缺少先例，经验和样本非常有限；同时，具备决定权的参数的确定往往涉及若干相互制约的指标和许多复杂的影响因素，需要权衡利弊，进行综合考虑。

在此，按照构建的层次结构将因素集按各自主要属性进行分类,对每一类进行综合评判,将评判的结果进行类之间的高层次综合[2]，最后引入具有决定权的参数权重，形成多层次模糊评判。

1.2 方案优选评定

1.2.1备选方案选择

为了克服传统方案选择中存在的盲目性等缺陷，使决策选择的方案更具科学性，降低决策分析的工作量，引入对抗性决策理念，进行方案不可行性的摈弃决策。首先通过专家经验问卷调查和既有施工案例的统计结果，仅从技术可行方面建立施工方法与结构形式的匹配关联库；其次，在前述建立的备选方案集中，以技术可行为先导，采用结构形式对逐个施工方案进行技术可行性碰撞，进行对抗否决的筛选形式，选择技术可行的施工方案，形成决策分析备选对象。

1.2.2数据标准化处理

桥梁上部结构快速更换方案优选决策因素中，有少量的定量指标，而更多的则是定性指标。

1) 定性指标。对于单个定性指标，如封闭交通对交通流量的影响，能够清楚地用数据或事实——[完全中断交通，严重拥堵堵塞，显著拥堵缓行通过，轻微缓行通过，无干扰通过][5]描述出各个级别不同，实现具体和清晰的界定，据此可以完成定性指标的评估，依照各个级别间的递进关系，在定性目标的论域[1，9]上来区分5个级别评定值。

2) 定量指标。对定量指标进行标准化处理，实现评价指标无量纲化和一致化，按其相对隶属程度均分为5个等级集，分别对应至定性目标的论域[1，9]上，分别给出5级评定值，使得定量指标也具有定性指标一致的评价值。

1.2.3模糊数学决策分析

根据4种标度的层次分析评定值，采用模糊数学评判法(TOPSIS、灰色关联分析法和熵值法等)[4]进行排序，进而根据Simpson的优势度指数[5]，给出满足目标准则状态下的推荐更换施工方法。

2 工程应用验证

武汉某高架桥于1997年10月1日建成通车，上部结构采用先张法预应力混凝土预制空心板，采用先简支后刚构连续混合体系，主桥长2 953.2 m，分为22联，桥面宽16 m。新建桥梁全长约14.6 km，双向八车道。依旧采用全线高架方案，标准段箱梁宽度33 m，上部结构采用预应力混凝土大悬臂展翅简支变连续箱梁，下部结构采用花瓶形双柱式桥墩[6]。

2.1 对抗性分析

既有旧桥为预制T梁，具有主梁间距过大、自重大、横向联系弱、腹板高而薄、横向刚度小等特点，排除分段切割等对抗性施工方案后，以控制爆破、整体移除和分单元移除为桥梁拆除备选方案；新建桥梁为预应力混凝土大悬臂展翅简支变连续箱梁，具有整体性好、自重大等特点，以满堂支架现浇、整体预制安装和移动模架现浇为桥梁安装备选方案。

结合既有桥梁和新建桥梁，本项目的快速更换组成有以下3个备选方案。

方案一M1，SPMT整体驮运法。以自行式模块运输平板车(简称SPMT)为核心设备，对既有旧桥上部结构进行整体顶升后，一次性驮运到拆解场地；对新建桥梁采用异地预制建造，成型后整体驮运至安装现场，整体安装。

方案二M2，控制爆破法+移动模架法。对既有旧桥——在预制T梁梁体内打孔装药，将桥梁上部结构直接炸断使其脱落或坍塌。对新建桥梁，采用可在桥墩上纵向移动的支架及模板体系，在其上逐跨现浇梁体混凝土，并逐跨施加预应力的施工方法。

方案三M3，分单元切割拆除法+满堂支架现浇法。对既有旧桥，选取高强度和高韧性的金刚石材料制成的绳锯，将T梁从预制梁间湿接缝位置切割分离，结合大型吊机进行调运至平板车，运至拆解场地后进行异地拆除。对新建桥梁，现场逐联搭设满堂支架，成型后再拆除支架，进入下一联施工工段，逐联开放交通。

2.2 构造判断矩阵

限于篇幅，以下计算仅以评价值为{1，3，5，7，9}的5级评定进行说明。根据层次分析法的基本原理，结合前述工程实际情况，按照“技术可行、交通影响小、安全可靠、工期可控和经济合理”的主次排序，构造指标体系中目标层对应于准则层的判断矩阵如下。

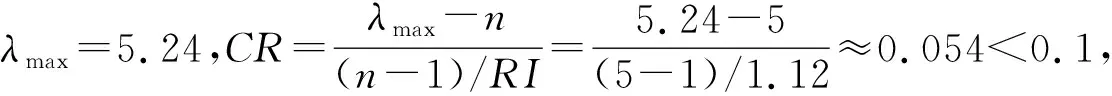
同理，可得各指标层的权重系数，各层权重计算结果见表1。

表1 桥梁更换方案优选指标权重

2.3 因素指标综合优选

根据优选指标体系，采用五级因素划分法，将指标按其性质分为{很差，差，中，良，优}5个级别，再赋以{1，3，5，7，9}量级集中对应的等级量值，构造初始决策矩阵C。

矩阵C中，每行表示各备选更换方案评价值，从第一行到第三行，顺次为方案一、方案二和方案三；每列表示一个指标因素项，矩阵元素表示该行指标的专家打分值。

2.3.1安全可靠指标评判

构造安全可靠指标初始评判矩阵。

进行标准化和归一化处理，得到加权标准化决策矩阵。

计算各方案基于安全可靠指标的贴近度，得到正理想解和负理想解为

则各方案与正理想解的贴近度为

2.3.2其余指标评判

与安全可靠指标计算过程相同，计算其余指标的加权标准化矩阵和贴近度，备选方案的加权标准化，以及贴近度计算结果见表2。

表2 更换方案优选指标评判值

续表2

从指标体系的5个准则层来看，安全可靠性最好的是方案二；技术可行性最好的是方案二；经济合理性最好的是方案三；交通影响性最优的是方案三；工期最合适的是方案三。

2.4 方法优选

在准则层各指标权重的基础上，引入决定性权重，提高施工需要封闭交通时间长的权重至0.667，继而对权重矩阵进行修正，确保满足施工封闭交通时间最短的首要目标；结合由各指标最优解贴近度构造得到评判矩阵，采用TOPSIS法则进而计算得综合优选结果向量F。

F=(0.298,0.504,0.476)

由上可知，在{1，3，5，7，9}的标度下，更换方案一至方案三的综合优劣顺序为：方案二、方案三、方案一。

2.5 多标度综合优选

经过同样的计算流程，在9/9～9/1标度和指数标度及10/10～18/2标度下，得到方案贴近度向量为E。

矩阵E中，每行表示备选拆除方案，从第1列到第4列，顺次为标度1～9、标度1～9、标度1～9和标度1～9下方案M1、M2、M3贴近度的向量。

由上方案贴近度向量E可得，4种标度下方案的优劣顺序一致，经Simpson的优势度指数公式得到方案的优越度分别为：18.4%，71.5%，52.8%，故选用方案二M2，与本工程最终采用的更换方案吻合。

3 结语

1) 借助模糊数学优选理论，不需要组织专家进行主观评价，从安全、技术、经济、交通，以及管理等多维度，建立了桥梁快速更换方案优选的多层多目标模糊优选模型。

2) 在对抗性分析的基础上，原始数据只需给出各自属性值，结合模糊数学综合评判法采用1～9标度、9/9～9/1标度和指数标度及10/10～18/2标度4种常用的[1,9]评分标度同时对层次单排序、总排序来评价快速更换方案的优劣性。

3) 根据4种标度的层次分析评定结果集，根据Simpson的优势度指数给出多准则状态下的推荐结果，较全面客观地评价了桥梁上部结构快速更换的推荐方案。

4) 为桥梁上部结构的快速更换施工方案决策提供科学依据，解决了方案决策管理程序和施工方案优选过程的冗长，并在一定程度上消除了在快速更换施工方案决策和评估标度选择上的盲目性和困惑，提供了一种新的、简洁、高效而实用的建模方法，从而更为有效地、快捷地指导方案决策工作。