基于改进AHP法的绿色建材评价指标权重研究
何经纶 魏先旺 欧卫星 杨建宇
(1长沙理工大学,湖南 长沙 4100761:2中国建筑第五工程局有限公司,湖南 长沙 410004)
推动建材绿色发展、对建材进行绿色性评价是建材行业当前一项重要研究课题。评价指标权重作为建材绿色性评价的重要参数,目前,决策者主要采用基于1~9标度的层次分析法(AHP)对其赋权,但1~9标度存在明显不合理的内在逻辑关系,权重计算也出现准确度不高的结果,且容易使判断矩阵与判断思维的一致性不统一,导致思维一致性程度并未被矩阵一致性指标真实反映出来[1-3]。
针对此种情况,左军提出了0~2 三标度法[4],徐泽水提出了-1~1 三标度法和-2~2 五标度法[5],汪浩等提出了9/9~9/1分数标度法和10/10~18/2分数标度法[6],侯岳衡等提出了90/9~99/9指数标度法[1]。本文对AHP标度方法进行改进,将模糊概念引入AHP的标度中,以指数标度表示模糊判断词,采用30/4~38/4指数标度构造判断矩阵,以提高判断矩阵指标值区分度和权重计算结果精确度,更准确地进行方案优选排序。
1 改进的AHP法
人们判断指标重要性的能力从心理学的角度来看是有限的,最多可以区分9个指标,当超过9个指标时,辨别就会变得模糊,很容易导致歧义和混乱。本文由此将重要性级别划为9个程度。通常,比较相同数量级指标的重要性是很简单的,所以吕跃进等将合适的重要性极限比设置为9[7],9也是本文选用最高标度等级。指数标度为30/4~38/4的层次分析法是本研究用来计算绿色建筑材料综合评价指数的权重的方法,以使计算的准确程度得以提高。
根据层次结构模型,采用30/4~38/4标度法及其倒数标度方法量化上级某一准则对与之相关联的下级指标两两相互重要性比较,九级标度法等级定义如表1所示。

表1 权重重要性的标度定义
2 30/4~38/4标度的比较分析
本研究采用顺序保证性、标度权重适用性、标度可记忆性、标度均匀性、标度可感知性、一致性等标准,对30/4~38/4的指数标度进行综合评价,对标度的利弊进行全面评估[8]。以下剖析典型的判定矩阵(由某一标度的所有标度值构成),比较1~9标度、9/9~9/1标度、10/10~18/2标度、90/9~98/9 标度及30/4~38/4 标度这四种常见标度,并评估30/4~38/4指数标度的利弊。
A1、A2、A3、A4、A5、A6、A7、A8、A9是当前被评价的一组对象,假设现在有一种情况:在某准则C下,A9、A8、A7、A6、A5、A4、A3、A2、A1与A1之间的重要性关系正好对应AHP法的九个等级,以此类推,得到在1~9标度、9/9~9/1标度、10/10~18/2标度、90/9~98/9标度及30/4~38/4标度下9个被评价对象的判断矩阵。
1)顺序保证性。被比较对象在不同数字标度下最大特征值及其特征向量利用MATLAB软件核算并进行归一化处理,结果如表2所示。
依表2所示,核算不同的标度下9个被评价对象得到的权重是不一样的,但是每一个特定标度的权重又都具备当i>k时Wi>Wk的性质,即下标大的权重大。由此可知,顺序保证性是所有标度法在单一准则下通用的性质。

表2 不同标度下所得的权重

表3 不同标度下CR、b、daverage
4)标度权重适用性。对于某一标度,权重差绝对值的平均值为:

其中,采用直接加权法核算得到的第i个标度值的权重用wiz表示,采用AHP法核算得到第i个标度值的权重用wib表示。则权重差绝对值的平均值daverage在不同标度下的核算结果如表3所示。明显可知,daverage越低,该标度具有更好的权重适用性。
根据表3所示,30/4~38/4标度是五种标度中一致性最优的,1~9标度是一致性最差的,介于两者之间的是分数标度和90/9~98/9指数标度,有着较好的一致性。1~9标度是五种标度中标度均匀性最优的,9/9~9/1标度是标度均匀性最劣的,介于二者之间的是分数标度和指数标度,标度均匀性较好。30/4~38/4指数标度是五种标度中权重拟合性最优的,权重拟合性次之的是90/9~98/9标度,1~9标度是权重拟合性最差的,介于二者之间的是全部分数标度。
具体到油气藏勘探对数字化技术的利用,中国地质大学(武汉)教授龚斌指出,油气勘探开发领域几乎所有数据是间接获得的,不确定性极强,而且干扰数据比较多,数据产生的对象和决策的对象是分离的。通过运用大数据做高精度地质建模、高效油藏数值模拟,通过人工智能等算法,在不断丰富的数据驱动下,实现模型持续更新,这样可以对地下油藏进行精确地描述,由此在充分考虑所有数据及认知的基础上,自动做出最科学、合理地预测和决策。
5)标度可记忆性和标度可感知性。1~9标度的标度值在五种标度中易于掌握和记忆,但是其余标度的标度值因为掺杂小数所以难以把握和记住,因此,1~9标度的标度可记忆性和可感知性最优的。
总结以上观点,顺序保证性是所有标度法在单一准则下的通用性质,相较于其他四种常见标度,有着最好的标度一致性、标度权重拟合性的是30/4~38/4指数标度,也有着相对来说较好的标度均匀性,然而有着相对较差的标度可感知性和标度可记忆性。由于90/9~98/9标度有着较大的核算误差,应尽量减少运用。本研究计算建材综合评价指标权重的方法采用基于30/4~38/4标度的AHP法,以完善权重计算的精准性。
3 计算指标权重
本文依据判断矩阵群对各评价指标的综合权重向量运用方根法进行计算。下面是采取群体层次分析法计算权重向量的过程。
1)权重在单人单准则下计算
2)综合权重在多人单准则下的计算
3)计算综合权重向量
根据上述计算结果由最低一级作为起点,从低到高找寻各级指标相对评价目标的重要性,二级权重×三级权重=单项权重w′,一级权重×单项权重=合成权重w′。
4 试验分析
本研究以砌体材料为评价对象,计算其评价指标权重运用的是基于30/4~38/4标度的群体AHP法。
1)建立递阶层次结构模型
从经济、技术、性能及全生命周期对环境产生影响的角度考虑,以砌体材料综合评价总体目标为依据,建立了递阶层次结构的评价体系模型,如图1所示。

图1 砌体材料综合评价指标体系
2)建立判断矩阵群
由10位建材领域的专家组成评价指标构建专家小组,判断矩阵群由小组成员共同建立。决策者们辨别对比某一准则下各指标相互之间的重要程度是依据评价指标递阶层次结构和判断矩阵构造方法完成的,以此形成决策者构造判断矩阵结果。
3)计算砌体材料综合权重
计算砌体材料评价指标的综合权重采用基于30/4~38/4标度的群体AHP法,根据前述计算结果得到专家小组各成员的评价指标权重和综合所有专家小组成员的评价指标权重,计算结果如表4所示。
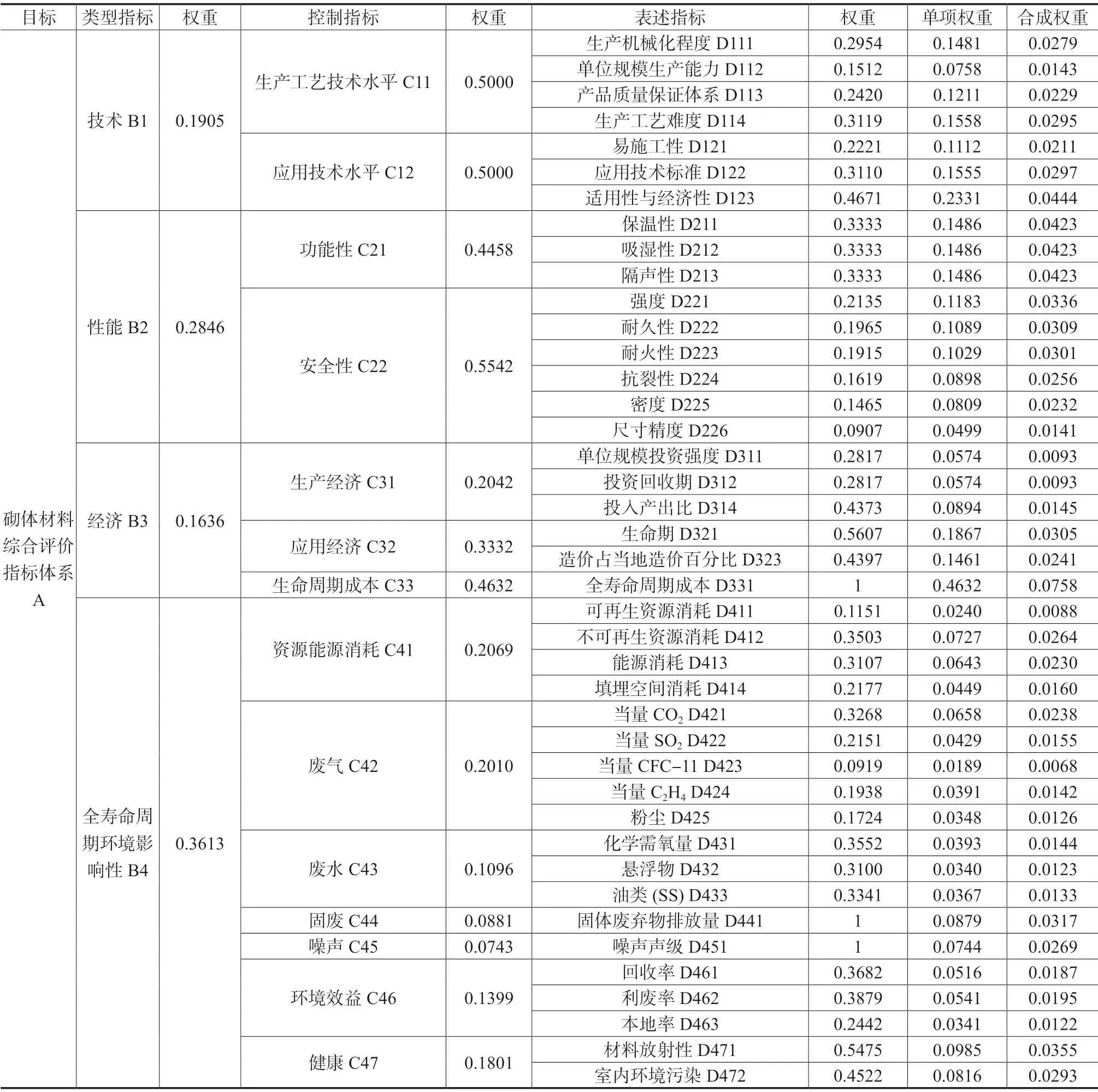
表4 砌体材料绿色综合评价指标权重
5 结语
本文利用改进的AHP标度方法,提出确定绿色建材综合评价指标权重方法为基于30/4~38/4 指数标度的层次分析法。通过剖析常见标度(1~9 标度、9/9~9/1 标度、10/10~18/2标度、90/9~98/9标度及30/4~38/4标度)的利弊,证实选取基于30/4~38/4标度的AHP核算的权重结果有着更高的精准度,且判断矩阵的一致性也被严格确保。同时,本文以砌体材料为研究对象,综合评价指标体系的判断矩阵由10位建材领域专家组成的专家小组共同创建,且各评价指标的综合权重选取基于30/4~38/4指数标度的群体AHP赋权法计算,证实了本文提出的基于30/4~38/4指数标度的层次分析法计算综合权重的准确性、客观性和实用性。

