层次分析法中两种标度的对比分析

舒孝珍

（成都师范学院 数学学院，四川 成都 611130）

美国运筹学家T·L·saaty 教授提出层次分析法是一种基于1-9 标度下的定性与定量分析相结合的系统决策方法[1]．在实际应用过程中，该标度下的层次分析法存在很多不足之处，因而，国内外学者对层次分析法的1-9 标度进行了改进，并且取得了丰硕的研究成果．目前的研究成果有：1-15 标度、x2标度、标度[2]、9/9-9/1 标度、10/10-18/2 标度、指数标度[3-4]、分数标度[5-6]等互反型标度，0-2 标度[7]、-1-1标度[8]、-2-2 标度[9]、0.1-0.9 标度[10]等互补型标度．如何分析比较不同类型标度在实际决策应用中的效益已成为众多研究者所关心的问题[11-14]．

对于标度的对比分析，吕跃进及其合作者对指数标度与1-9 标度进行了对比研究，得到指数标度与1-9 标度在一致性上是互不相容的，前者效果优于后者，且前者具有优良的数学结构[15]．骆正清和杨善林提出了用保序性、一致性、标度均匀性、标度可记忆性、标度可感知性、标度权重拟合性6 个标准对常见的7 种互反型标度进行了比较，得到对于解决单一准则下的排序问题，保序性对所有标度都成立，指数标度的一致性和权重拟合性最好[16]．1-9 标度法的标度均匀性、标度可记忆性、标度可感知性这3个性质最好．刘颖芬和占济舟论证了1-9 标度、a8= 9 标度、9/9-9/1 标度、10/10-18/2 标度的完全一致性互不相容，得到a8= 9 标度比其他几种标度更为合理[17]．以上的研究主要集中在“互补型”标度的对比方面，但很少有研究针对“互反型标度”和“互反与互补型”标度进行深入研究.因此，在前人的研究方法基础上，文章对应用最广泛的互反型1-9 标度与互补型0.1-0.9 标度进行了对比研究，得到了如下的结论：1- 9 标度和0.1- 0.9 标度这两种标度法都具有保序性和一致性，1/9 标度的均匀性比0.1-0.9标度要好，而权重拟合性比后者差.

1 两种标度的关系

在实际应用中，互反型1-9 标度与互补型0.1-0.9 标度是应用广泛的两种标度，二者的关系如表1 所示.

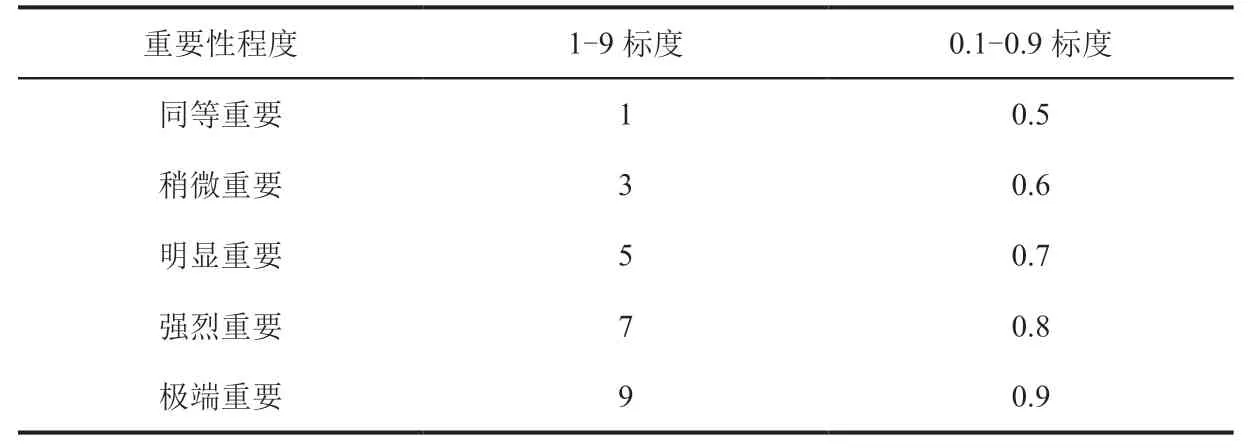
表1 1-9 标度与0.1-0.9 标度的关系

2 两种标度的比较

2.1 保序性

保序性的数学定义如下[16]：对某一排序决策问题D，有n个被比较对象A1,A2, ... ,An，它们在准则C下存在一个客观次序R，现利用某一标度S对问题D进行排序，如果得到的排序结果与客观次序R相同，则称标度S对排序决策问题D具有保序性.

现建立一组被比较对象：A1,A2,A3,A4,A5．不失一般性，假定在某准则C（即构造一个新的标度：1-5标度）下的客观次序是A1与A1,A2,A3,A4,A5之间的关系恰好构成：同等重要、稍微重要、明显重要、强烈重要、极端重要．A2与A2,A3,A4,A5之间的关系恰好构成：同等重要、稍微重要、明显重要、强烈重要．A3与A3,A4,A5之间的关系恰好构成：同等重要、稍微重要、明显重要．A4与A4,A5之间的关系恰好构成：同等重要、稍微重要．A5与A5之间的关系恰好构成：同等重要．

根据以上关系，可以得到这5 个被比较的对象在1-5 标度的判断矩阵，如表2 所示.

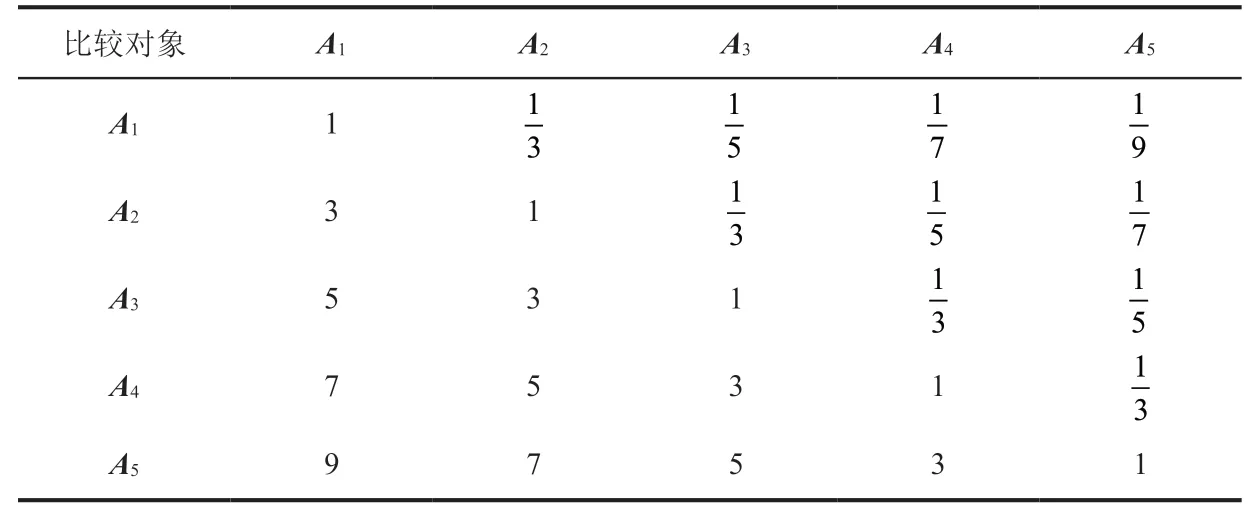
表2 1-5 标度下的判断矩阵

根据表2，把1-9 标度下的5 个标度值作为被比较的5 个对象，可得它们1-5 标度的

利用MATLAB 编写程序cxl1.m

Z=[1 1/3 1/5 1/7 1/9;3 1 1/3 1/5 1/7;5 3 1 1/3 1/5;7 5 3 1 1/3 9 7 5 3 1];

[V,D]=eig(Z)

W=V(:,1)/sum(V(:,1))

lambda=max(eig(Z))

n=size(Z)

CI=(lambda-n)./(n-1)

RI=1.12

CR=CI./RI

if CR＞=0.1

error;

else ’pass text’

end

运算结果：

lambda=5.2375，W=（ 0.0333 0.0634 0.1290 0.2615 0.5128)，CI=0.0594，CR=0.0530，ans=pass text

根据表2，可得0.1-0.9 标度下的5 个标度值作为被比较的5 个对象，并且可得其在1-5 标度下的判断矩阵为：

根据上述判断矩阵，利用MATLAB 编写程序cxl2.m

Z=[0.5 0.4 0.3 0.2 0.1;0.6 0.5 0.4 0.3 0.2;0.7 0.6 0.5 0.4 0.3;0.8 0.7 0.6 0.5 0.4; 0.9 0.8 0.7 0.6 0.5];

[V,D]=eig(Z)

W=V(:,1)/sum(V(:,1))

lambda=max(eig(Z))

运算结果：

lambda=2.808，W=(0.1123 0.1562 0.2000 0.2438 0.2877 ).

由上述运算结果，可得1-9 标度与0.1-0.9 标度的权重，如表3 所示.

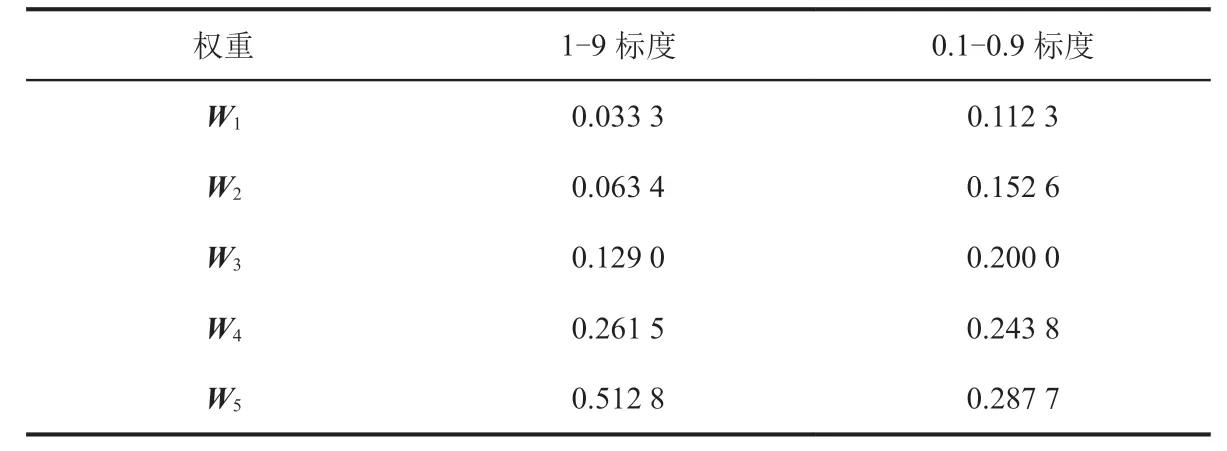
表3 1-9 标度与0.1-0.9 标度的权重

由表3 可知，1-9 标度与0.1-0.9 标度的权重虽然不同，但是当它们同在1-5 这个任意特定的标度下，权重又都具有如下性质：Wi＞Wj，当i＞j时，即下标小的权重小，由此可知，对1-5 这个标度下的排序问题，1-9 标度与0.1-0.9 标度都具有保序性.由此，得到如下结论：对单一准则下的任何排序问题，1-9标度与0.1-0.9 标度，这两种标度都具有保序性.

2.2 一致性

层次分析法中判断矩阵的一致性，主要用来评判决策者在作出定性判断时是否保持前后一致．在互反型判断矩阵中，若矩阵中的元素满足aik×akj=aij，则称判断矩阵为一致性矩阵．但在实际应用中，决策者做出的定性判断往往不是完全一致的，因而引入了一致性指标CR作为衡量判断矩阵一致性的标准，并规定当CR= 0 时，判断矩阵具有完全一致性；当CR＜ 0.1 时，判断矩阵的一致性在可以接受的范围；当CR＞ 0.1 时，判断矩阵的一致性不符合要求．

一致性指标CR的计算方法如下：

其中，RI是平均随机一致性指标，可通过查表得到.λmax是判断矩阵的最大特征值，aij=aik－ajk＋0 是判断矩阵的阶.

在互补型判断矩阵中，若判断矩阵中的元素满足aij=aik－ajk＋0.5，则称判断矩阵是一致性矩阵.根据杜栋教授在文章[10]和徐泽水教授在文章[18]中的分析，可以得到：原始互补型判断矩阵A= (aij)n×n，通过以下数学变换[19]，可以得到一致性判断矩阵B= (bij)n×n，从而可以避免一致性检验.

其中，i,j= (1,2,...,m)，m为单准则下的元素个数.

另外，徐泽水教授在文章[18]中指出，若A= (aij)n×n是互反型1-9 标度下的判断矩阵，则可以通过公式（2）

转换为互补型0.1-0.9 标度下的判断矩阵B= (bij)n×n.

反过来，若B= (bij)n×n是互补型0.1-0.9 标度下的判断矩阵，则可以通过公式（3）

转换为互反型1-9 标度下的判断矩阵A= (aij)n×n.

由上述分析可知，1-9 标度与0.1-0.9 标度这两种标度的判断矩阵的一致性是相同的．对于1-9 标度的判断矩阵，通过2.1 节中的MATLAB 软件运算结果，可以看到一致性指标：

满足一致性，从而0.1-0.9 标度的判断矩阵也满足一致性.

2.3 标度均匀性

标度均匀性是指在某一标度下，所有相邻的两标度值的差或商大致相等的程度[16]．为了比较1-9 标度与0.1-0.9 标度这两种标度的均匀性，引入如下关于标度均匀性的定义.

定义1[16]某一标度下相邻的标度值差dij为：

其中，Si，Sj为某一标度下相邻的两个标度值.

定义2[16]某一标度下相邻的标度值商Dij为：

其中，Si，Sj为某一标度下相邻的两个标度值.

定义3[16]某一标度下标度值差的距离d为该标度下最大标度值差与该标度下最小标度值差的差：

定义4[16]某一标度下标度值差商的距离D为该标度下最大标度值商与该标度下最小标度值商的商：

定义5[16]某一标度的标度值距离的平衡值为：

当1.1 ≤b≤ 2.0 时，标度均匀性比较理想；当2.1 ≤b≤ 6.0 时，标度均匀性比较好；当b取其他值时，标度均匀性比较差.

根据上述定义，现在分别考察1-9 标度与0.1-0.9 标度，这两种标度的均匀性．

对于1-9 标度，所有的dij= 2，故标度值差的均匀性好，标度值差的距离d= 2．标度值商分别为D31= 3，D53= 1.67，D75= 1.4，D97= 1.29．标度值商的距离D= 2.33.因而平衡值b=1.16，标度均匀性较为理想.

对于0.1-0.9 标度，所有的dij= 0.1，故标度值差的均匀性好，标度值差的距离d= 0.1．标度值商分别为D31= 1.2，D53= 1.17，D75= 1.14，D97= 1.13．标度值商的距离D= 1.06．因而平衡值b= 10.6，标度均匀性较差.

根据以上分析表明，1-9 标度的标度均匀性优于0.1-0.9 标度的标度均匀性.

2.4 标度权重拟合性

定义6[16]标度权重拟合性是指用层次分析法计算的权重与用标度值直接加权的权重的拟合程度.我们可以引入以下公式来判断一个标度权重拟合性的优劣.

其中，Wbi表示用层次分析法得到的第i个标度值的权重，Wzi表示用直接加权法得到的第i个标度值的权重，n表示某一标度下标度值的个数．当Eavg越小时，表明该标度的权重拟合性越好．

利用上述权重拟合性优劣公式以及通过表3 和直接计算两种标度的权重，可以得到1-9 标度与0.1-0.9 标度的权重拟合程度，如表4 所示.

表4 1-9 标度与0.1-0.9 标度的权重拟合度

表4 表明，1-9 标度的权重拟合度比0.1-0.9 标度的权重拟合度差.

3 结 语

关于1-9 标度和0.1-0.9 标度，文章从标度的保序性、一致性、均匀性、权重拟合性这4 个方面对两种标度法进行了对比分析．结果表明，在标度的保序性和一致性这两方面，1-9 标度和0.1-0.9 标度的都具有良好的保序性和一致性；在标度均匀性方面，1-9 标度优于0.1-0.9 标度；在标度的权重拟合性方面，0.1-0.9 标度优于1-9 标度．

文章通过对1-9 标度和0.1-0.9 标度进行分析比较，目的在于帮助决策者在利用层次分析法去解决实际问题时，可以根据具体情况入手，有针对性地选择恰当标度去解决问题，从而避免在标度选择上的盲目与无所适从.