任意阶算子的有理逼近—奇异标度方程

郭钊汝， 何秋燕， 袁 晓， 蒲亦非

(1.四川大学电子信息学院， 成都 610064； 2.四川大学计算机学院， 成都 610064)

1 引 言

近年来，分数阶微积分理论与应用在电磁学、流体力学、图像处理、声音处理等众多领域都引起了广泛关注.具有分数阶微积分运算功能的元器件称为分抗元(Fractor).理想阶分抗元的阻抗函数为

I(μ)(s)=F(μ)sμ(0<|μ|<1,s∈C)

(1)

式中，μ为运算阶数(Operational order)；s是运算变量，又称复频率或拉普拉斯变量；F(μ)是分抗元的集总特征值—分抗值(Fractance)，简称分抗；sμ称为μ阶微积分算子，当μ取分数(0<|μ|<1)时，将sμ称为分数阶微积分算子，简称分数阶算子或分数算子[1].

为了叙述简洁方便而又不失一般性，定义归一化运算变量(也称归一化频率变量) .

w=τs=s/Ωτ

(2)

式中，τ为时间常数；Ωτ为对应的特征频率.由此可将理想分抗元的阻抗函数归一化为

(3)

归一化变量w与函数ι(μ)(w)均为量纲一的量.(归一化)算子wμ是一个无理函数[1].因此，算子wμ的有理逼近就转化为了一个数学问题：构造一个有理函数序列{yk(w)，(k∈N)}，收敛于一确定的极限阻抗函数y(w)，即有

(4)

式中，极限阻抗函数y(w)等于ι(μ)(w)的逼近称为理想逼近，在一定条件下或一定频率范围内近似等于ι(μ)(w)的逼近称为非理想逼近.

人们提出二项式展开法[2-3]、连分式展开法[4-5]、Padé有理逼近法[6]等方法构造算子wμ的迭代函数.本文根据连分式展开法，利用标度拓展理论[1,7-9]推出一组全新的非正则标度方程—奇异标度方程(Strange Scaling Equation).目的考察奇异标度方程在迭代过程中，所获得的有理函数序列{yk(w)}是否满足分抗逼近所必须满足的基本性质与运算性能.通过零极点分布探究物理可实现性、运算振荡现象和运算振荡周期.

2 标度拓展理论与奇异标度方程

2.1 半阶算子迭代方程

半阶算子w±1/2的有理迭代逼近过程[7-11]，以及许多经典的半阶分抗逼近电路(比如Oldham分形链电路[12]，Carlson分形格电路[7-8]等)可用简单的代数迭代方程—半阶算子迭代方程式(5)来描述.

y(w)=F(y(w))

(5)

即给定一个恰当的初始有理函数y0(w)=N0(w)/D0(w)，由迭代函数F(·)可以得到

(6)

2.2 标度拓展—任意阶算子与非正则标度方程

文献[1]根据半阶有效的Oldham分形链分抗与任意阶有效的Liu-kaplan分形链分抗的对比分析发现，描述Oldham分形链分抗电路的代数迭代方程(5)是描述Liu-kaplan分形链分抗电路的非正则标度方程(Irregular Scaling Equation)的特例.由此袁晓[1]提出由半阶算子迭代方程直接标度化生成非正则标度方程：

(7)

即可用来描述任意阶算子wμ的有理逼近过程.式中正实数α，β称为标度特征参量，σ=αβ称为标度因子(Scaling Factor).当取0<|σ|<1称为反比拓展，当取1<|σ|<称为正比拓展[1,7-9].

根据标度拓展理论，文献[7]将全频有效的半阶Carlson分形格分抗电路拓展到任意阶标度分形格电路，文献[13-14]提出任意阶格形标度分数忆阻概念与电路实现.这些成果说明，标度拓展是获得任意阶算子有理逼近的一种有效手段.

2.3 连分式展开法与奇异标度方程

连分式展开法[15]有理逼近的理论基础是恒等关系.

(8)

(9)

分别令

(10)

则得到两个半阶有效的(代数)迭代方程

(11)

(12)

容易验证，上述两组迭代方程构造的迭代过程

(13)

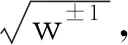
(14)

满足计算有理性，运算有效性[1,7].

对迭代方程(11)，(12)分别进行标度拓展，得到两组非正则标度方程—I型奇异标度方程

(15)

与II型奇异标度方程

(16)

显然，该组方程满足计算有理性.也即是说，给定初始有理函数y0(w)时，迭代生成有理函数序列

(17)

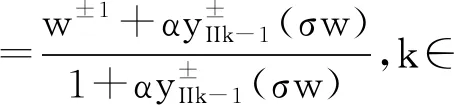
(18)

计算有理性(Computational Rationality)是构建分抗的有理函数序列yk(w)的基本要求.因为在分抗逼近电路中，应当使用可获得的基本电路元器件—整数阶元器件，而尽可能避免使用分抗元器件.

那么，奇异标度方程的有理函数序列yk(w)(式(17)，(18))是否具有分抗逼近所必须满足的运算有效性与物理可实现性成为下节要探究的问题.

3 运算有效性—奇异标度方程的近似求解

运算有效性是指非正则标度方程y(w)=F(αy(σw))的真实解(Actual Solution)，也即迭代过程(给定初始有理函数y0(w))

yk(w)=F(αyk-1(σw)),k∈+

(19)

判定非正则标度方程的运算有效性，是分抗有理逼近或者标度方程描述的过程或系统是否具有分数阶运算功能或分数阶过程与现象的核心问题.但对于非正则标度方程[9,16]运算有效性的准确求解(特别是解析解的获得)是一个极具挑战性的课题[1].为了考察运算有效性，在不知如何求得真实解的情况下，只有采用近似求解法，考察奇异标度方程(15)和(16)的近似解是否包含简单的算子wμ项.

3.1 I型奇异标度方程的近似求解

在极端条件下，对于I型奇异标度方程(15)有

(20)

因此，在极端频率条件0←|w±1|<<1下，得到近似解

(21)

而在极端频率条件1<|w±1|→时，方程(15)简化为一个准正则(quasi-regular)标度方程

(22)

并有近似解析解(approach analytic solution)

(23)

近似解析解(23)表明，方程(15)描述了一个半阶算子的运算有效性.

如果α=1,σ≠1，则有奇异标度方程

(24)

显然，这是一个半阶有效的非正则奇异标度方程.

3.2 II型奇异标度方程的近似求解

对于II型奇异标度方程(16)，在极端频率条件下有

(25)

在极端频率条件1<<|w±1|→下，近似得到一个准正则标度方程

(26)

并有近似的解析粗解

(27)

另一方面，在极端频率条件0←|w±1|<<1时，近似得到一个标准的(normal)正则标度方程

(28)

并有近似的解析解—Liu氏粗解[1]

(29)

这两种近似解的结果表明：II型奇异标度方程，不但描述了一种任意阶算子的运算有效性—近似解为Liu氏粗解(29)，而且还描述了半阶算子的运算有效性—近似的解析粗解为式(27).

4 运算性能和逼近性能—奇异标度方程的数值求解

近似求解只能判定奇异标度方程的运算有效性.数值求解能够直观地探究奇异标度方程迭代生成的有理函数序列所描述的运算性能和逼近性能.

4.1 数值求解算法—系数矢量序列迭代算法

根据式(4)，以I型奇异标度方程迭代生成的有理函数序列(17)为例，有

(30)

记分子多项式Nk(w)和分母多项式Dk(w)的系数矢量[1,7]为

βk=[βknk,βknk-1,...，βk0]

(31)

αk=[αknk,αknk-1,...,αk0]

(32)

并定义等次扩项运算

(33a)

(33b)

和增次扩项运算

(34a)

(34b)

则得

(35)

同理求得两类奇异标度方程的有理函数序列的系数矢量序列，整理于表1中.

表1中，算符∘：等长矢量的点积运算；顶标算符=：等次扩项；顶标算符←：增次扩项.

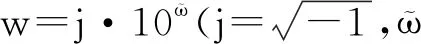
yk(j·10ϖ)=Ak(ϖ)exp(j·θk(ϖ))

(36)

幅频特征

Ak(ϖ)=|yk(j·10ϖ)|

(37a)

Λk(ϖ)=lgAk(ϖ)

(37b)

相频特征

θk(ϖ)=Arg{yk(j·10ϖ)},ϖ∈R，

(38)

阶频特征

(39)

表1 奇异标度方程的迭代算法公式

Tab.1 Iterative algorithm formulas of the strange scaling equations

y±k(w)βkαky+Ik(w)αk+αk-1σk-1←αk-1σk-1+αβk-1σk-1y-Ik(w)αk+αk-1σk-1αk-1σk-1←+αβk-1σk-1←y+IIk(w)αβk-1σk-1+αk-1σk-1←αk-1σk-1+αβk-1σk-1y-IIk(w)αβk-1σk-1←+αk-1σk-1αk-1σk-1←+αβk-1σk-1←

运算性能由相频特征和阶频特征完全表征.接下来以初始阻抗y0(w)=1为例，对比标度拓展前后的频域特征曲线来着重考察奇异标度方程迭代生成的有理函数序列的运算性能与逼近性能[17].

4.2 I型奇异标度方程迭代生成的有理函数序列的运算性能分析

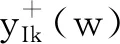
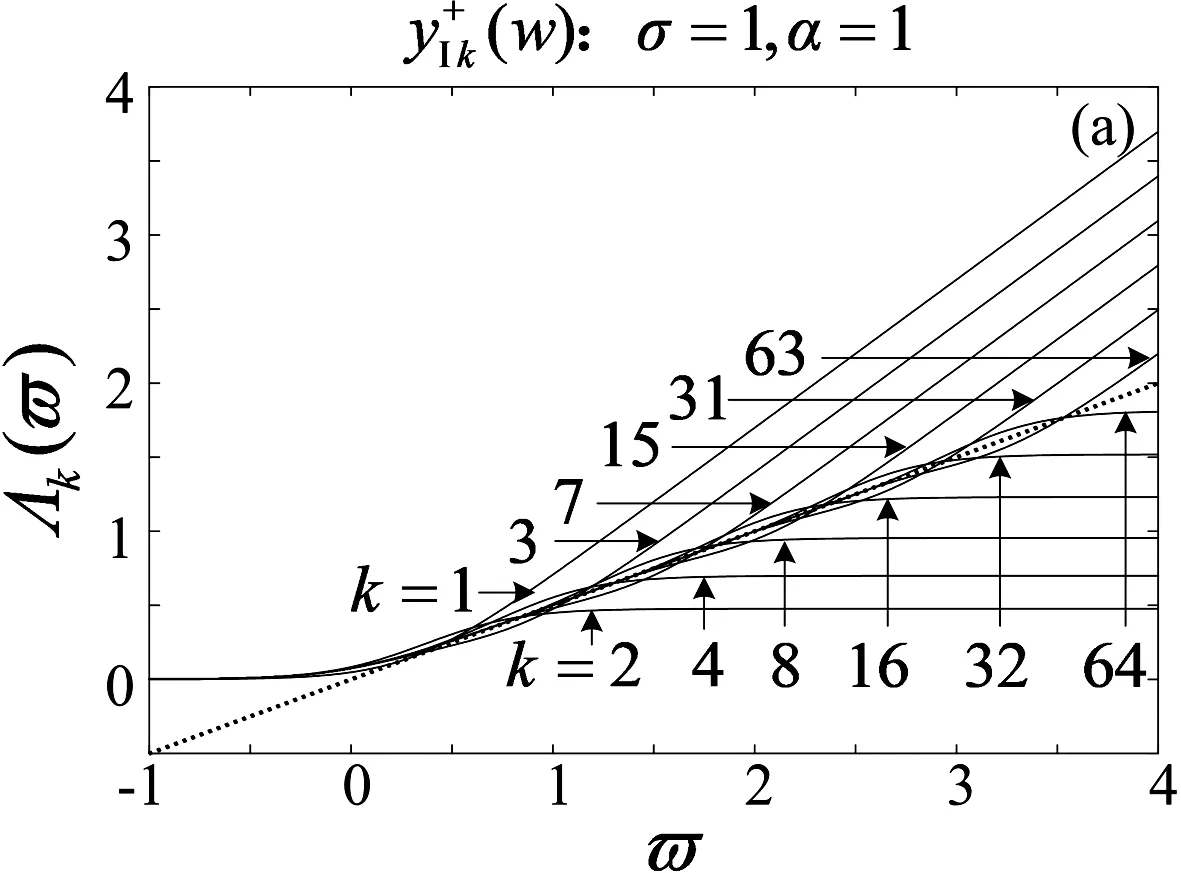
图1 标度拓展前的频域特征

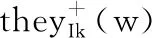
(a) Amplitude-frequency characteristics; (b) phase-frequency characteristics; (c) order-frequency characteristics

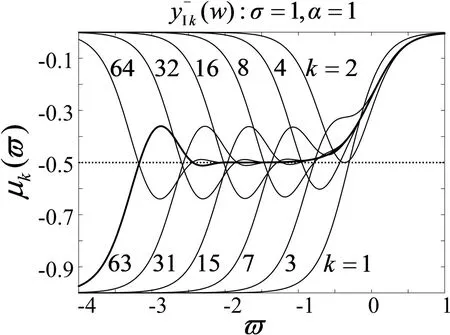
图2 标度拓展前的阶频特征

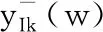
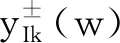
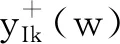
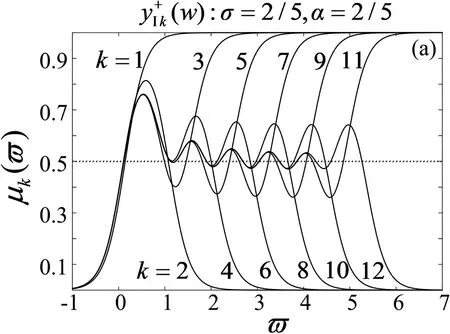
图3 标度后的阶频特征

Fig.3 Order-frequency characteristics after the scaling

(a) Proportional expansion; (b) inverse expansion

4.3 II型奇异标度方程迭代生成的有理函数序列的运算性能分析

II型奇异标度方程，既描述了一种半阶算子的运算有效性，又描述了任意阶算子的运算有效性—这是标度拓展理论的升华.

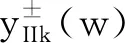
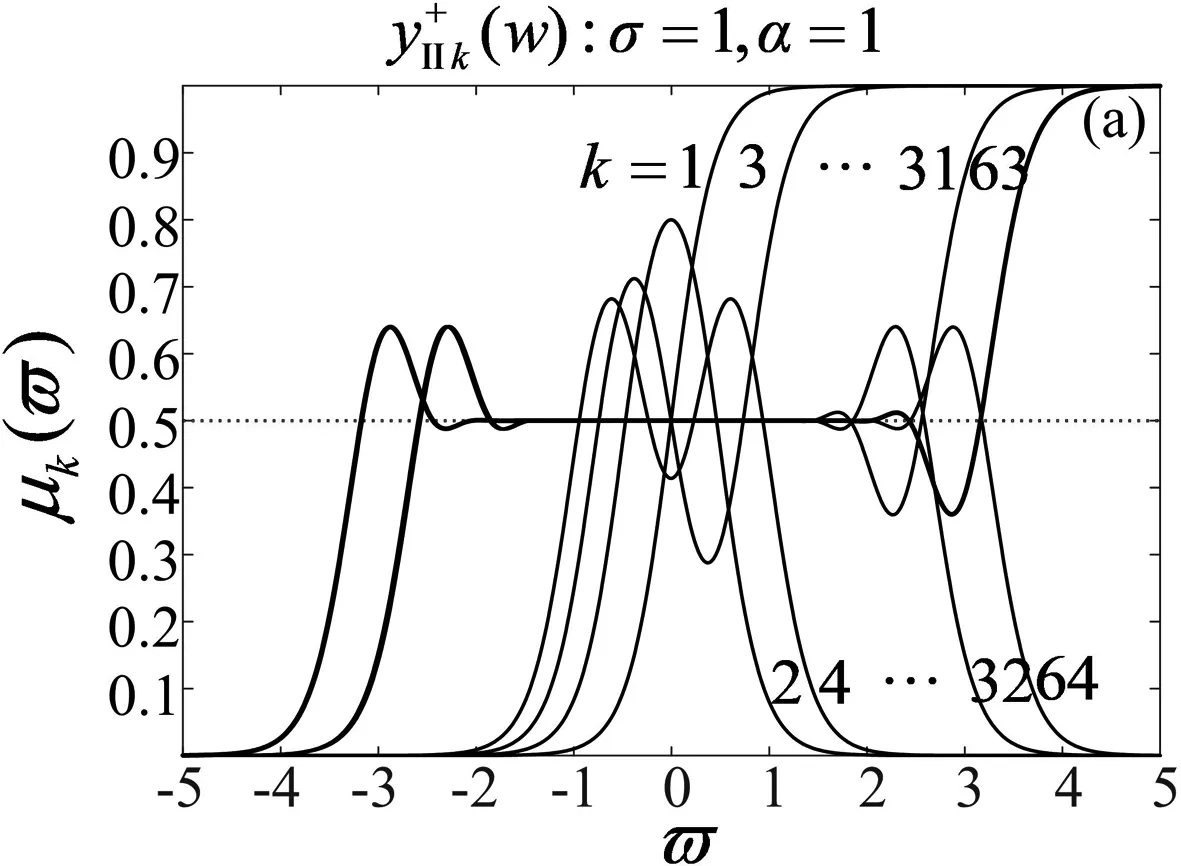
图4 标度拓展前的阶频特征

Fig.4 Order-frequency characteristics before scaling expansion

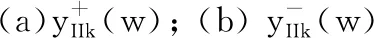
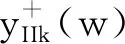
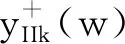
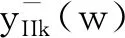
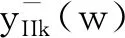
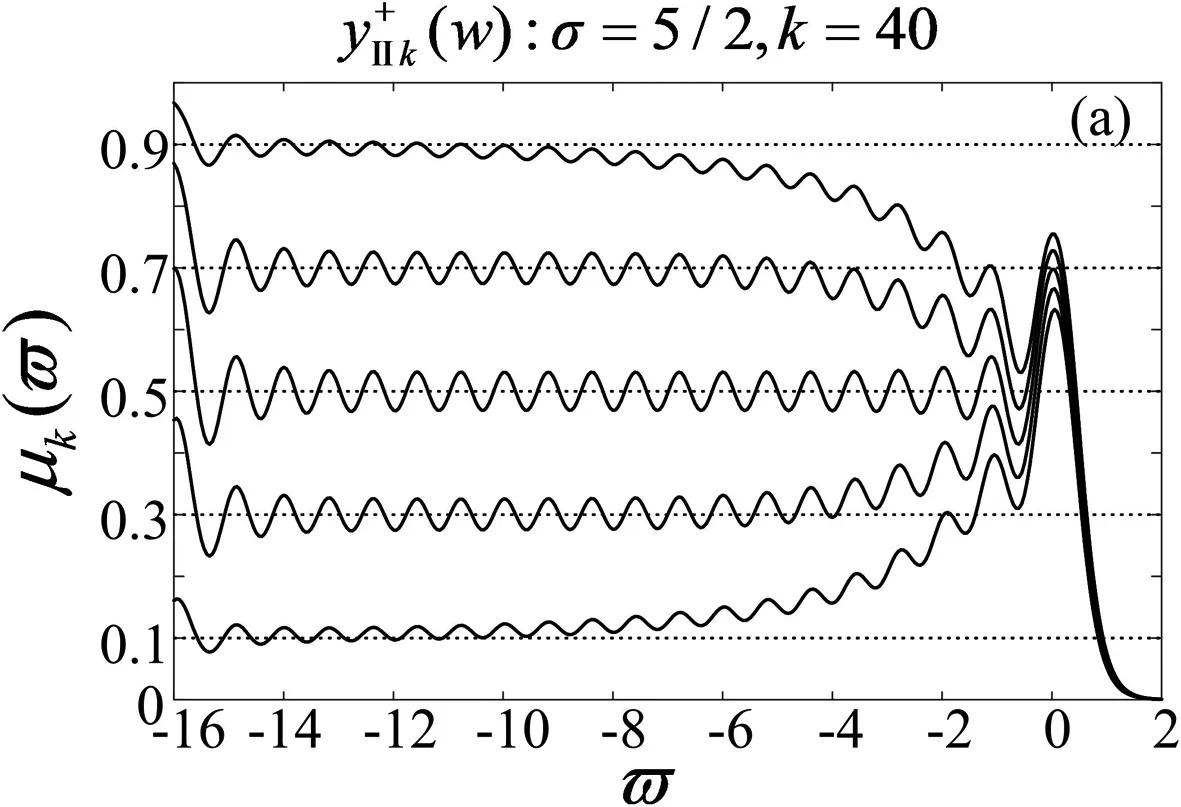
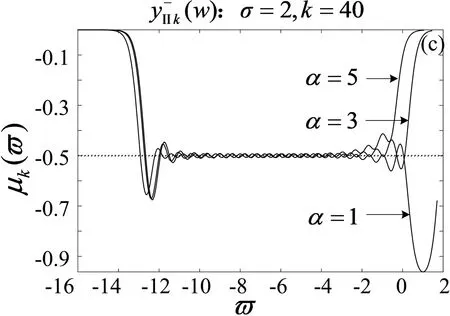
4.4 奇异标度方程迭代生成的有理函数序列的逼近性能分析

(40a)

(40b)

奇异标度方程的本征Κ指标为Κ=lg4.

标度拓展后，I型和II型奇异标度方程迭代生成的有理函数序列的逼近带宽指数分别为

(41a)

(41b)

奇异标度方程的运算振荡周期W=2|lgσ|.

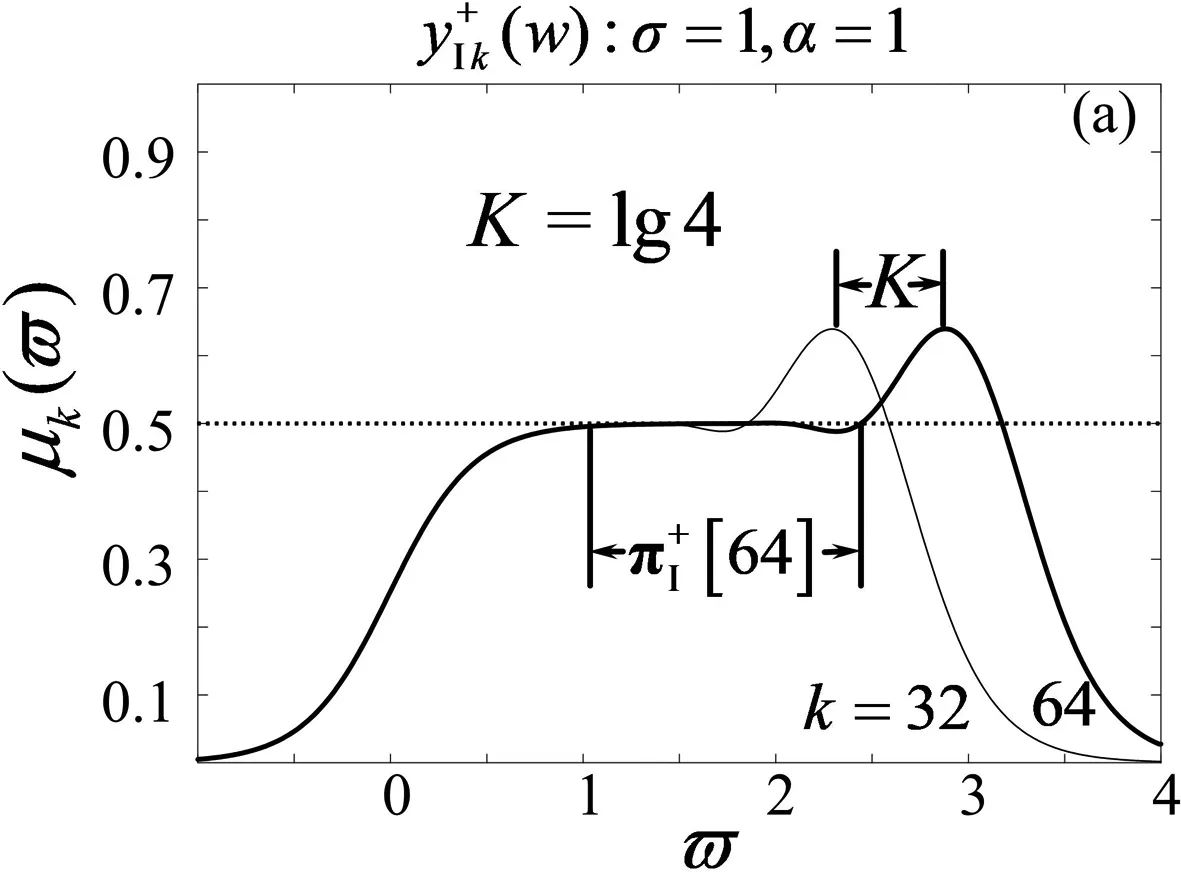
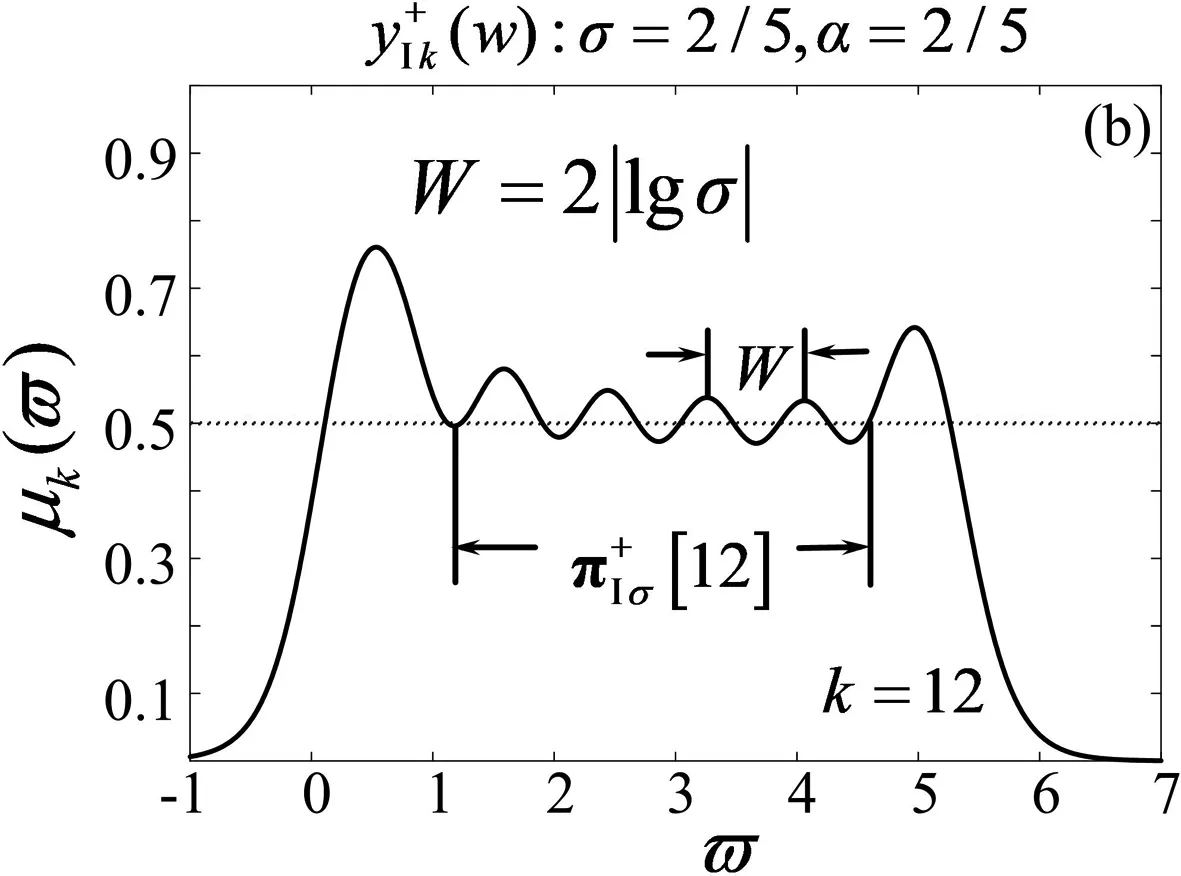
图的阶频特征

逼近效益(approximation benefit)—逼近带宽指数与迭代次数之比.标度拓展前，逼近效益分别为

(42a)

(42b)

标度拓展后，逼近效益分别为

(43a)

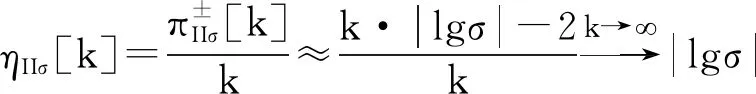
(43b)

拓展增益(extension gain)能够定量表征标度拓展后相对于标度拓展前获得的更高的逼近效益程度.

(44a)

(44b)

由此可见，标度拓展极大地提高了逼近带宽和逼近效益.

标度拓展后的逼近带宽指数和逼近效益与迭代次数k以及运算振荡周期W密切相关，下一节将介绍运算振荡现象和运算振荡周期.

5 奇异标度方程的零极点分布—物理可实现性与运算振荡现象

奇异标度方程迭代生成的有理函数序列{yk(w),k∈}可表示为

(45)

其中，zi为零点值；pi为极点值. k次迭代后，分别对应有k/2个零点，k/2个极点，交错成对出现.

在复平面内的零极点分布[18]决定了奇异标度方程迭代生成的有理函数序列yk(w)的物理可实现性.根据零极点频率指数与运算特征的局域化特征关系，可分析运算振荡现象和运算振荡周期.

5.1 物理可实现性

物理可实现性要求阻抗函数的零极点或是在复平面(即黎曼曲面的主叶)的负实轴上，或是共轭成对出现在复平面的左半平面.复平面零极点分布在实轴上为强逼近，分布在虚轴上为弱逼近，阻抗函数在整个复平面上达到一致收敛—强逼近要求往往难以实现[1].

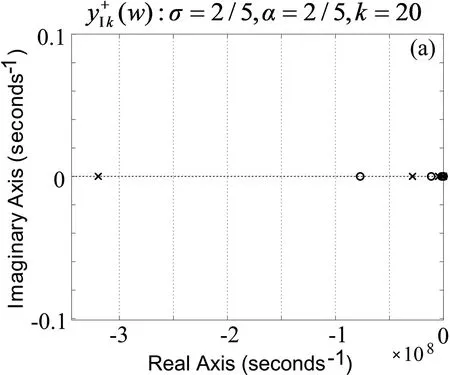
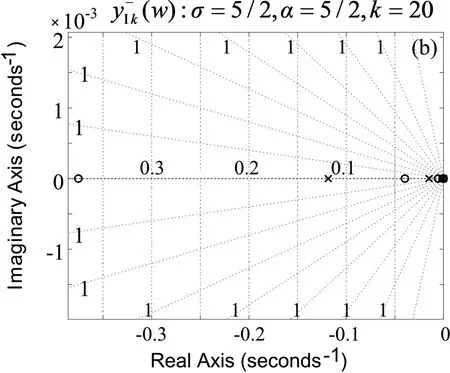
图7 I型奇异标度方程在复平面内的零极点图

Fig.7 Zero-pole map in complex planes of the type I singular scaling equations

5.2 运算振荡现象

为了更好地观察和探究奇异标度方程有理函数序列yk(w)的零极点分布规律，根据零极点频率指数oi和χi与零极点关系式

(46)

得到有理函数序列的零极点频率指数分布(如图8和图9)，令第i对零极点频率指数为第i个一次子系统Ei(w)，那么一次子系统Ei(w)的频域特征函数——相频特征.

(47)

阶频特征

(48)

具有偶对称性和局域化特性(图8(a))，正是这种每个一次子系统都会产生波峰的局域化特性，使得有理函数序列yk(w)在频域产生了准周期性的运算振荡现象，运算振荡现象是所有一次子系统的集体行为，如图8(b)所示.

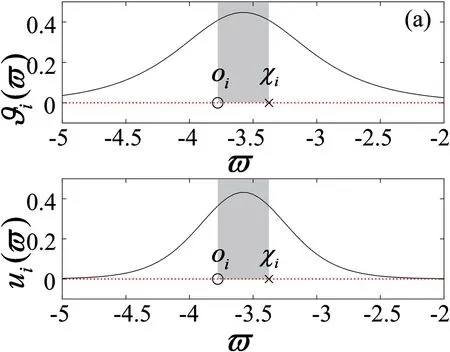
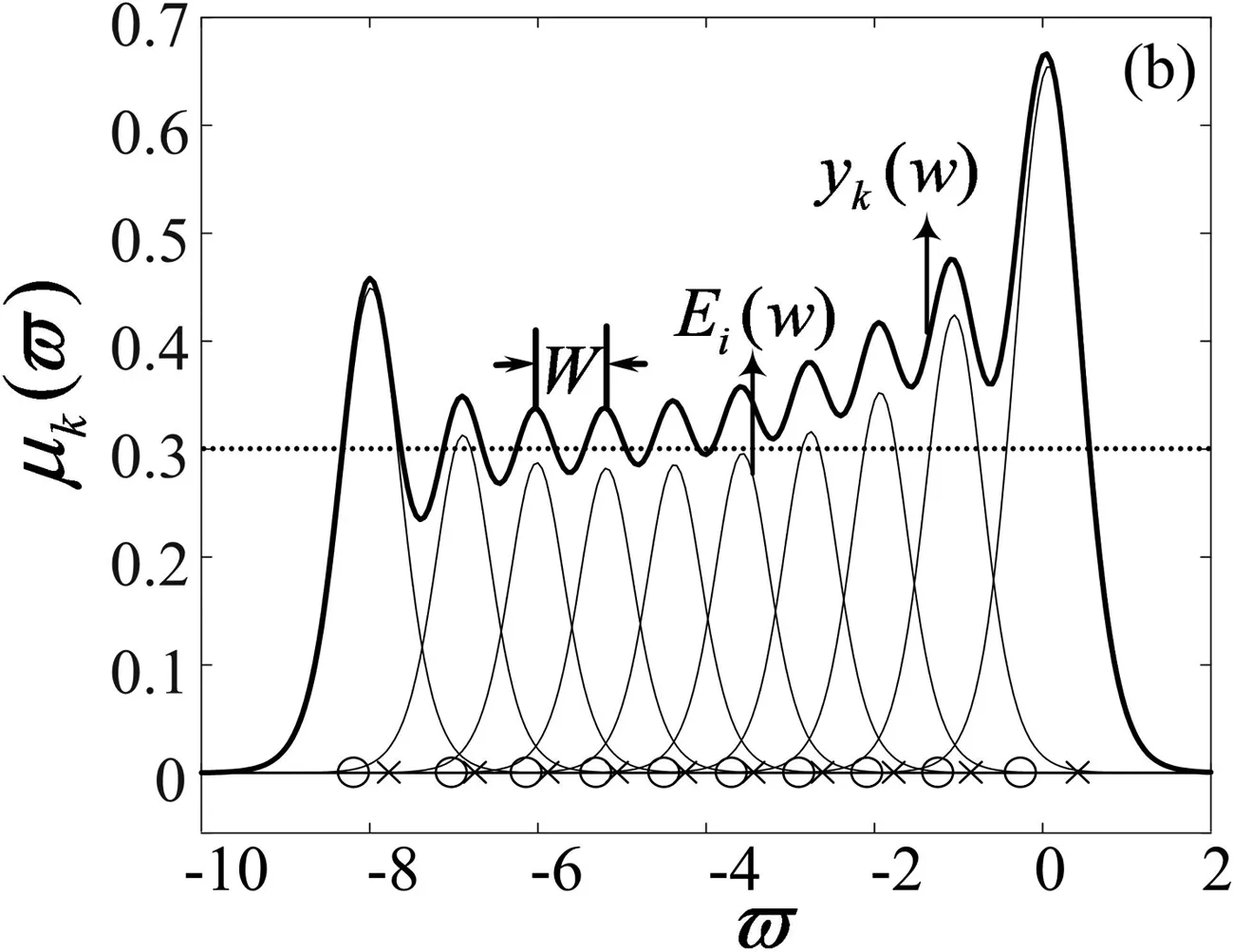
图8 频域特征与零极点频率指数的关系

(a) 一次子系统Ei(w)的局域化特性；(b) 阶频特征的运算振荡现象

Fig.8 The relationship between frequency performance and Zero-pole frequency index

(a) localization performance of the primary subsystem Ei(w); (b)operational oscillation of the order-frequency characteristics

奇异标度方程，Oldham分形链，Carlson分形格等经典的逼近过程均有准周期性的运算振荡现象. 拓展来说，任何一个具有物理意义或源自于物理可实现系统的非正则标度方程，必定存在具有准周期性运算振荡现象的真实解．

下一节将介绍奇异标度方程迭代生成的有理函数序列yk(w)的每个一次子系统之间的距离，也就是运算振荡周期W是多少.

5.3 运算振荡周期

同理可得，两类奇异标度方程的有理函数序列的运算振荡周期都为W=2|lgσ|.这与大多数描述标度化电路的非正则标度方程(格形标度方程等[19]、Hill标度方程[20]、Liu-Kaplan标度方程[21])真实解的运算振荡周期W=|lgσ|不同，这是奇异标度方程的有理函数序列的另一奇特性质.

表2 I型奇异标度方程迭代生成的有理函数序列的零极点频率拟合方程

Tab.2 Zero-pole frequency fitting equations of the iterative generation’s rational function sequences of the type I strange scaling equations

标度因子运算振荡周期(2lgσ)零点频率指数拟合方程极点频率指数拟合方程y+Ik(w)σ=0.52lg0.5≈0.602 1oi=-0.64i+6.8χi=-0.64i+7.1y-Ik(w)σ=52lg5=1.397 9oi=-1.4i+0.95χi=-1.4i+0.16

6 结 论

通过方根连分式法和标度拓展理论得到的奇异标度方程的运算性能，呈现与以往所了解的方程不同的运算有效性：奇异标度方程能够等程度地、均匀地、平稳地向高频段或低频段逼近算子wμ.I型奇异标度方程的运算阶与标度因子无关，是半阶算子的非理想逼近过程.II型奇异标度方程是理想逼近过程，受标度因子的影响，在高频或低频域内，运算阶可以是半阶算子，也可以在一定条件下严格限定逼近任意阶算子.

根据两类奇异标度方程迭代生成的有理函数序列{yk(w)}，探究运算性能、逼近性能、物理可实现性与运算振荡周期方面的特别之处.并解释了物理可实现系统的非正则标度方程的运算振荡现象.由奇异标度方程迭代生成的有理函数序列，用系数矢量序列迭代算法得到的频域特征图，验证了近似求解的运算阶的正确性且归纳了逼近带宽指数、逼近效益和拓展增益，I型与II型奇异标度方程迭代生成的有理函数序列标度前后的逼近效益都因标度拓展有了极大地提高.由零极点分布，得到两类奇异标度方程迭代生成的有理函数序列是强逼近且物理可实现的.运算振荡周期和标度因子有关：W=2|lgσ|.

奇异标度方程包含了十分丰富的内容，关于奇异标度方程还有许多问题值得深入研究.用K线图、O、P指标与逼近带宽量化挖掘奇异标度方程的其他奇特性质，搭建该方程的对应电路.找寻奇异标度方程在流体力学、黏弹力学、图像处理、声音处理、忆阻等方面的应用.