钢筋混凝土柱抗爆动力分析简化方法

杨 明 夏雨帆

(中交第二公路勘察设计研究院有限公司 武汉 430063)

随着恐怖袭击和偶发爆炸事故造成的桥梁爆炸事故不断增加，桥梁结构抗爆安全问题越来越受到关注。然而现有桥梁在设计过程中很少考虑桥梁的抗爆安全性，也无桥梁抗爆方面的相关规范要求[1]。为此，国内外学者开展了大量研究，并取得了一定成果：上世纪40年代，美国安全委员会出版了《美国陆军安全技术手册TM5-855-1》[2]；Williamson[3-5]等对钢筋混凝土桥墩进行抗爆模型试验和有限元模拟，提出了公路桥梁桥墩抗爆构造要求；国内吴亮等[6]对近场爆炸时RC(钢筋混凝土)墩柱的动力响应开展了参数化研究；李国强等[7]进行了民用建筑的抗爆分析，并提出相应的设计规范。上述有限元模拟或者试验研究，对爆炸荷载作用下钢筋混凝土(reinforce concrete,RC)墩柱的动力响应分析具有重要意义，但由于有限元模型建立和试验模型设计的复杂性和与局限性，在桥梁抗爆设计中并不实用，只能作为验证手段。因此，本文提出了一种快速、精确计算结构在爆炸冲击荷载作用下最大反应的方法。

1 理论分析

爆炸荷载是一种荷载作用大、持续时间极短的冲击荷载，结构承受爆炸荷载与承受周期性荷载或谐振荷载相比，阻尼对控制结构的最大反应显得不太重要[8]。所以在研究柱体结构的抗爆分析时，可不考虑阻尼的影响。

1.1 运动偏微分方程

RC柱在爆炸荷载作用下的受力示意见图1。

图1 承受动力荷载的墩柱受力示意

综合微段水平方向的动力平衡关系式和微端下端的弯矩平衡方程，以及弯矩和曲率之间的关系式，可导出RC柱在爆炸荷载下的运动偏微分方程，如式(1)。

(1)

式中：m(z)为柱体的线质量；N(z)为作用在截面上的轴力；v(z,t)为平行于截面上的横向力；EI(z)为墩柱的截面抗弯惯性矩；p(z,t)为作用在柱体上的爆炸荷载。

墩柱是桥梁结构中的关键承重构件，其完整性对桥梁的安全与运营有直接影响。在设计中，墩柱竖向承载力通常能满足甚至远大于实际需求，在实际情况中，墩柱更多是被“摇倒”而很少被压溃，轴向力的存在可以提高墩柱的抗弯能力，所以研究墩柱在横向爆炸冲击荷载作用下[9]的最大反应时偏安全地不考虑轴向力的作用，在考虑墩柱截面性质不变的情况下，m(z)、EI(z)取为定值m、EI。则式(1)可以化简为式(2)形式。

(2)

1.2 等效单自由度体系

实际上RC墩柱都是连续分布体系，位移形式有无数多种，所以上述求得的RC墩柱的运动偏微分方程有无数多个解，每个解对应1种振型。求解每个振型的精确解较困难，而且很不经济。在许多工程实际问题中，设计师们并不需要求解出结构的所有振型，而只较为关心结构前几阶较低的自振频率。特别是在冲击荷载作用下，墩柱迅速达到最大反应，一般只需考虑其第一阶振型。因此，将连续分布体系简化成单自由度计算较低频率就显得很有意义了。等效单自由度体系只允许墩柱有单一的变形形式，并使得到的结果与真实值差别不大，与该自由度关联的质量、刚度、荷载称为等效质量Me、等效刚度Ke、等效荷载Pe。将体系转化为等效单自由度体系后，其分析方法与单自由度体系完全一样。

根据伽辽金原理可以求解式(2)得式(3)。

(3)

式中：φ(z)、p(z)为动荷载沿跨度变化及随时间变化的特征函数；w(z)为假定的挠度分布形式也称形函数；函数v(t)为描述结构位移随时间的变化规律的动力函数。

则式(3)可简化为

(4)

式(4)是关于单个正则坐标v(t)常微分方程，它与单自由度体系强迫振动的常微分方程完全相似。

对于爆炸冲击荷载，式(4)的解为

(5)

式中:τ为爆炸荷载作用到柱体表面的时间；Ie为等效荷载冲量，ωe为自振角频率。

(6)

(7)

最终可以得到动力位移表达式，如式(8)。

y(z,t)=w(z)v(t)=

(8)

等效单自由度计算流程图见图2。

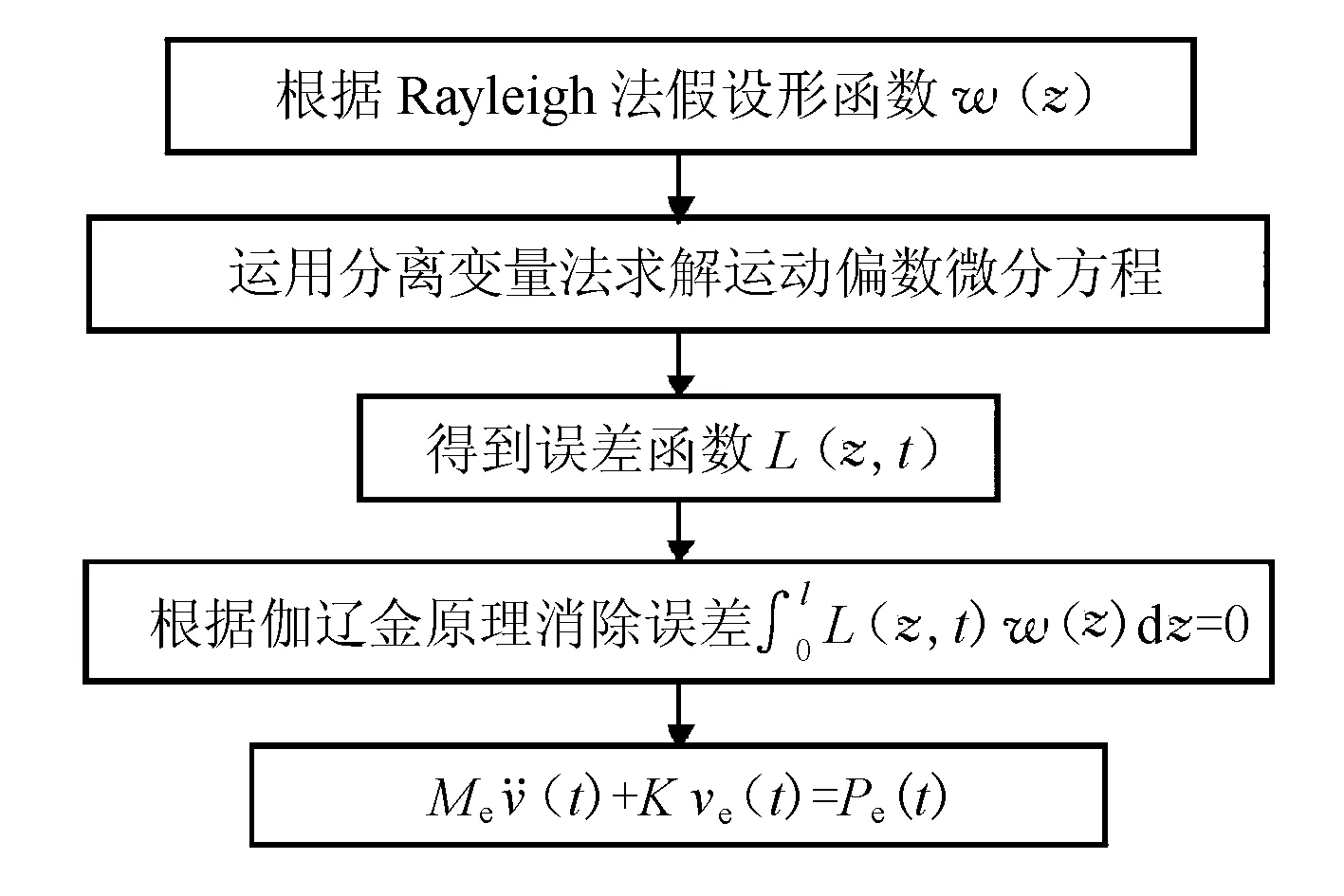
图2 等效单自由度计算流程图

2 固端柱的计算

柱体在爆炸荷载作用下必然产生一定程度的破坏，只允许柱体发生弹性变形很不经济；在实际工程中，柱体在爆炸荷载作用下发生一定的塑性变形，但不影响结构的正常使用，或者经修复后可以正常使用，对工程师来讲，都是可以接受的。这里以两端固接、等截面RC柱为例，研究柱体在均布爆炸荷载下的最大塑性变形。固端柱的工作特点是在支座和中部截面处均有可能出现塑性铰，而且出现的时间一般不同，其先后次序取决于支座截面与中部截面刚度的比值。在正常配筋条件下，一般先在支座处形成塑性铰，然后在柱体中部出现塑性铰[10]。固端柱在爆炸荷载作用下的变形过程示意见图3。

图3 固端柱在爆炸荷载作用下的变形过程示意

2.1 弹性阶段的计算

p(z,t)沿跨度均匀分布，则式(3)中φ(z)=1，根据固端柱的边界条件z=0和z=l处，y=0和y′=0可得

(9)

式中：τ为爆炸荷载到达柱体表面的时间；ω1为弹性阶段一阶振型的自振角频率，计算方法见式(10)。

(10)

主体端部能承受的最大弯矩为M0(常数)，爆炸荷载作用下端部荷载超过最大弯矩时会形成塑性铰，出现塑性铰的时间t1可通过式(11)求得。

(11)

2.2 弹塑性工作阶段计算

在时间t>t1后，固端柱的两端出现塑性铰，则柱体支座处等效有2个集中力矩(M0)作用的简支梁，且除柱体两端外，其他位置均属于弹性阶段。该阶段计算工作同2.1弹性工作阶段计算。

在时刻t=t1时，柱体两端达到塑性极限弯矩M0，出现塑性铰，式(11)可改写为式(12)。

(12)

设该阶段的动力挠度曲线方程为

yz(z,t)=w2(z)v2(t)+w1(z)v(t1)

(13)

此时在边界条件z=0和z=l处，y=0和EIy″=M0。

在此基础上可求得挠度曲线为

(14)

解得动力函数为

(15)

式中：ω2为弹塑性变形阶段的一阶振型的自振角频率，计算方法见式(16)。

(16)

柱体的中部出现塑性铰弯矩也为M0，则出现塑性铰的时间t2可由式(27)求得

(17)

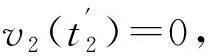
(18)

2.3 塑性阶段计算

如果在某一时刻t2满足式(17)，则在跨中截面处出现塑性铰。塑性阶段时，柱转化为由塑性铰相联结的2根绝对刚性的半梁，在柱体端部和柱中部有附加集中力矩M0。

设塑性阶段梁的动力挠曲方程为

y3(z,t)=w1(z)v(t1)+w2(z)v2(t2)+φ(t)z

(19)

运用虚位移原理可求得以转角表示的运动方程

(20)

(21)

(22)

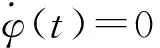
塑性阶段结束时，柱体中部达到的最大位移ym，为

(23)

等效单自由度法的优势在于可以快速、准确地得到结构的最大变形，为结构抗爆设计提供依据。墩柱抗爆设计流程图见图4，设计者只需输入墩柱的几何性质(弹性模量E、截面惯性矩I、线质量m、墩柱高度l)、墩柱的边界条件、考虑应变率效应得到的极限弯矩M0、爆炸荷载冲量大小Ie和墩柱中部最大容许位移yd，即可验证设计是否满足抗爆要求。

图4 墩柱抗爆设计流程图

3 有限元验证分析

3.1 有限元模型

本文采用AUTODYN有限元软件对RC柱进行数值模拟，柱体高3.4 m(其中柱净高3 m，柱头和柱脚分别高0.2 m)。设置柱头和柱脚可以避免钢筋从混凝土里拔出，也便于在柱的两端施加牢固的固端约束，爆炸模型示意图见图5。柱体的主筋采用8根直径18 mm的HPB300钢筋，箍筋采用10 mm的HPB300钢筋，在柱头和柱脚箍筋的间距为100 mm，柱中箍筋的间距为200 mm。钢筋混凝土柱的网格大小为20 mm，钢筋与混凝土通过Lagrange-Lagrange耦合。爆炸荷载采用平面布置，平面起爆，以便产生均匀荷载。在钢筋混凝土迎爆面上布置7个测点(测点1～7)，间距为50 cm；在钢筋混凝土中心布置11个测点(测点8～18)，间距为30 cm。空气采用欧拉单元建立，网格大小为20 mm，空气与钢筋混凝土柱通过Lagrange-Euler耦合。

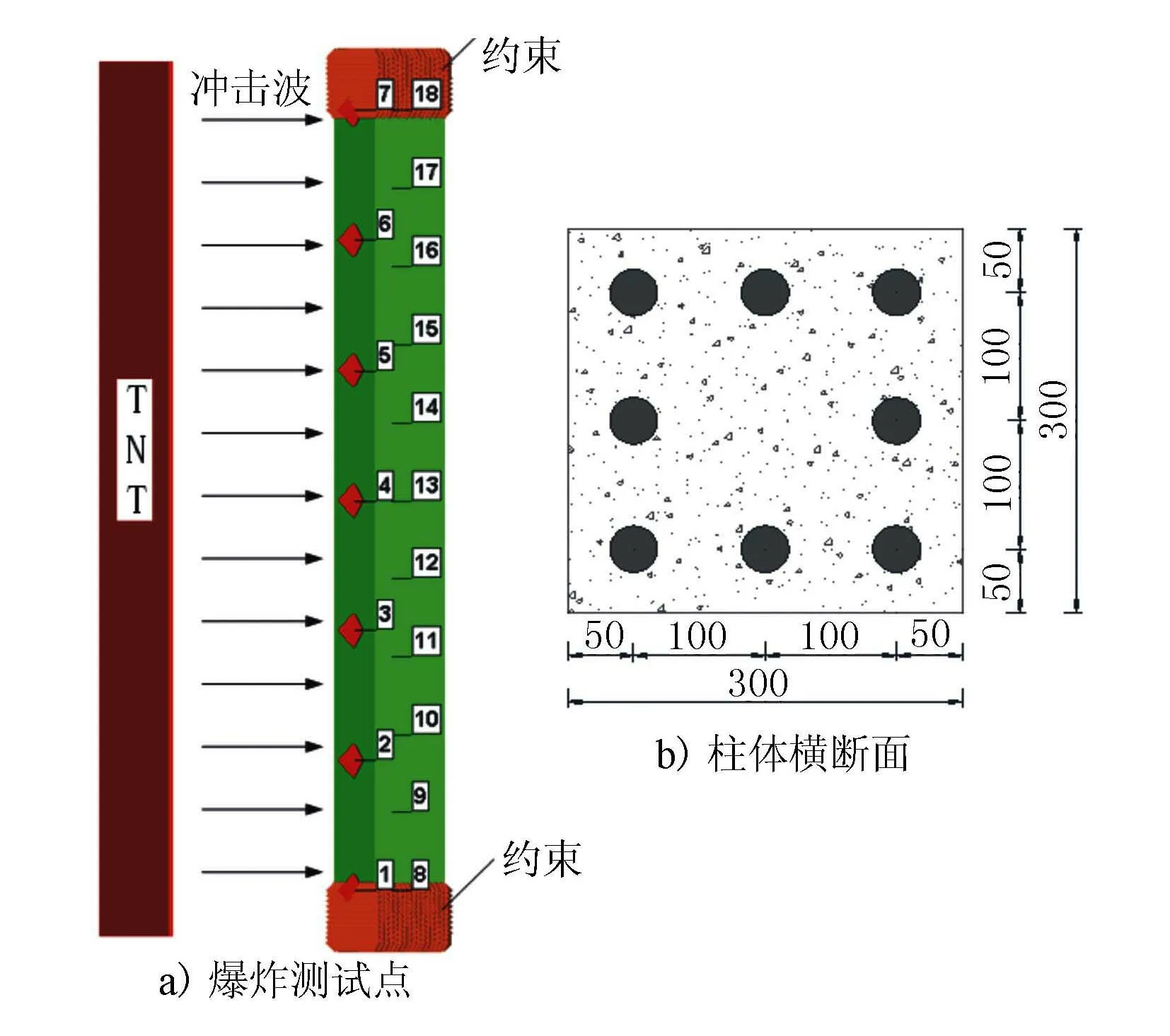
图5 爆炸示意图、测点布置示意图与柱体横断面示意(单位：mm)

3.2 建模材料

混凝土材料采用CONC-35 MPa，空气材料选用理想气体，钢筋材料选用STEEL4340，爆炸荷载通过引爆TNT产生，材料参数见表1、表2。

表1 CONC-35 MPa材料性质

表2 STEEL 4340材料性质

3.3 有限元结果

爆炸荷载作用下，迎爆面2～6号测点的超压时程曲线图见图6。

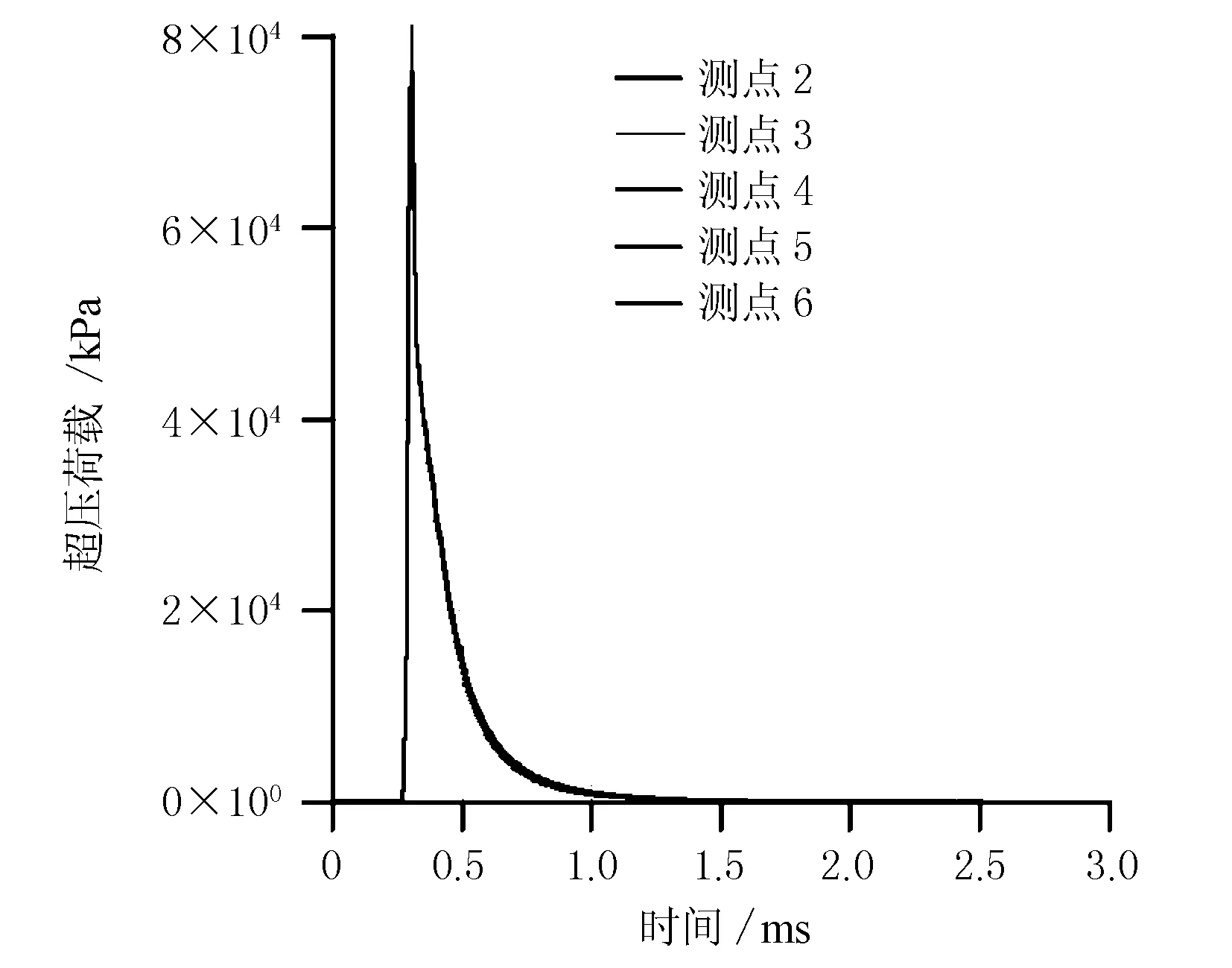
图6 测点2～6号测点的超压时程曲线

由图6可以看出2～6号测点的超压时程曲线完全重合，说明在迎爆面上，爆炸荷载作用在柱上的荷载是随时间变化的均布荷载，超压峰值为81.1 MPa，到达峰值的时间为0.3 ms，其后快速衰减，整个作用时间极短不超过1.5 ms。柱体任一截面的累积荷载冲量为10.0 MPa·ms，爆炸荷载冲量图见图7。

图7 爆炸荷载冲量

在均布爆炸冲击荷载作用下，柱体的挠度时程曲线图见图8。由图8可见，各测点的振动趋势一致，振幅从柱的两端到柱的中部逐渐增大，且关于柱中部对称。在短暂的爆炸冲击荷载下作用后，柱体开始振动，在12.6 ms时，柱体的变形达到最大，柱的中部位移值为77.0 mm，之后快速衰减，最后趋于稳定值(4 mm)，有一定的残余变形，表明柱体已经发生了塑性变形。且从图中可以看出，振幅衰减很快，经过一两个周期后，柱体停止振动，表明柱体结构在塑性阶段耗能很快，这有利于结构在爆炸荷载中幸存。

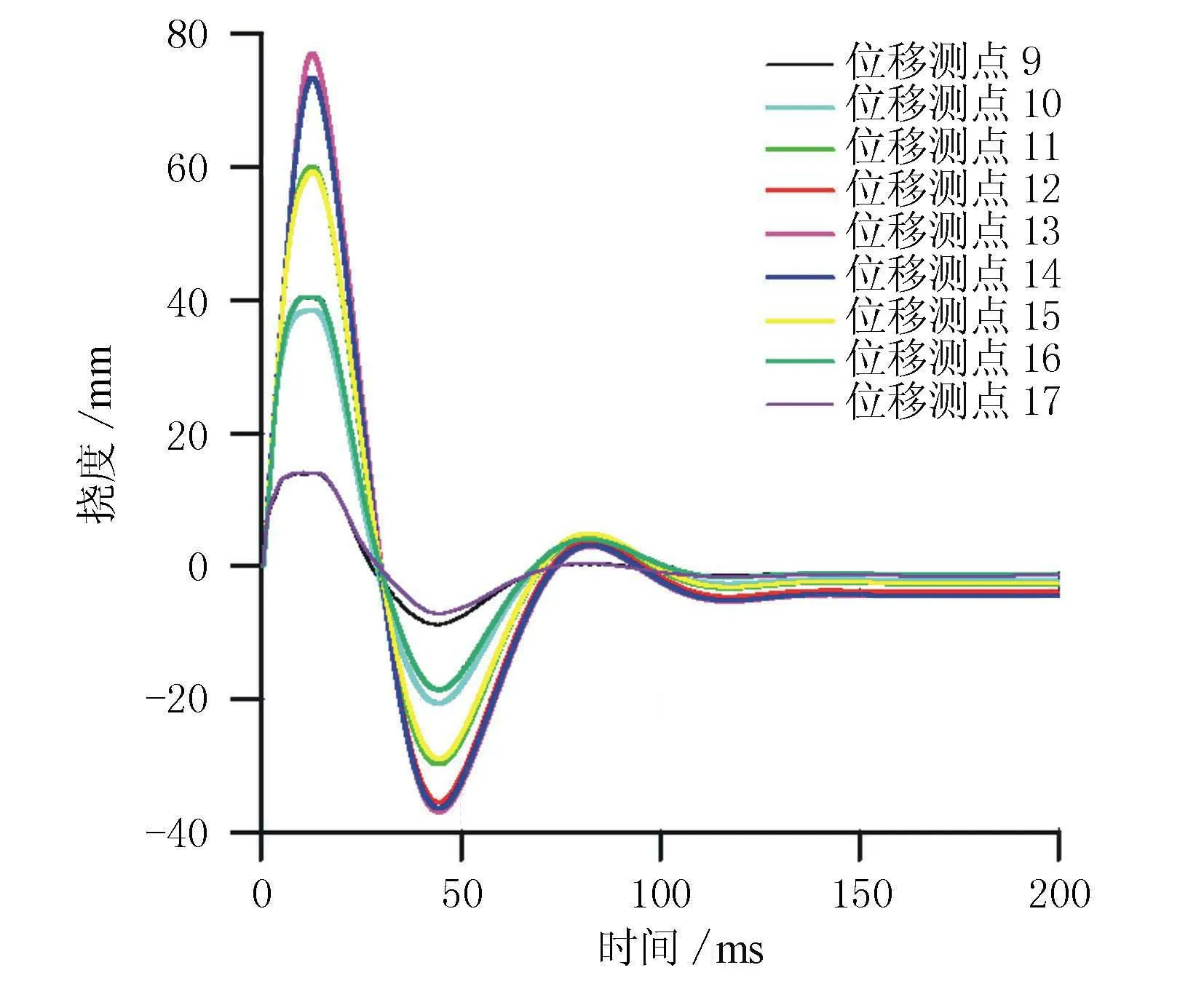
图8 柱体挠度时程曲线图

3.4 理论计算结果与仿真结果对比

将爆炸荷载及钢筋混凝土柱的各参数带入到固端柱计算理论可以得到墩柱挠度值，理论计算值与仿真值对比结果见图9、图10。

图9 墩柱中部测点理论计算最大变形与仿真结果对比图

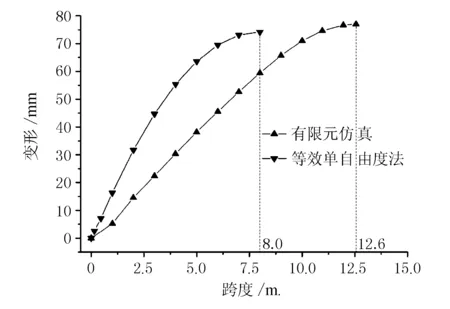
图10 墩柱中部测点理论计算振型与仿真结果对比图

由图9可见，通过等效单自由度法与有限元计算结果相差不大，两者在变形图上有略微差距，有限元得到的变形图比较平滑，而等效单自由度法得到的变形图在柱中部地方不平滑，这是因为理论简化分析时，将塑性铰理想化为集中在柱中部的点，而实际塑性铰是一段区域，这对最后结构影响不大。在RC墩柱跨中位置：简化单自由度计算结果为74.2 mm，有限元计算结果为77.0 mm，误差为3.6%。由图10可见，理论计算振型和仿真计算结果，两者振动趋势一致，幅值有略微差别，两者到达最大变形的时间区别也极小，仅相差4.8 ms，减去爆炸冲击波传播和作用在结构上的时间，两者的差距会进一步缩小。

4 结语

本文介绍了一种快速、精确计算结构在爆炸冲击荷载作用下动力响应的方法：等效单自由度法。并以RC墩柱为研究对象，详细介绍了RC墩柱在爆炸荷载作用下动力响应的理论计算过程，最后结合有限元数值模拟验证了该理论方法的有效性和可行性。这种方法可以快速地计算墩柱在爆炸荷载作用下的动力响应和抗爆能力，设计工作者只需输入爆炸荷载的大小、边界条件、墩柱的几何尺寸、截面性质等参数，即可求解出桥墩的振型、振动频率和最大动位移，为桥墩抗爆设计提供依据。