多连拱形迎爆面对结构抗爆效果的影响
祝小龙
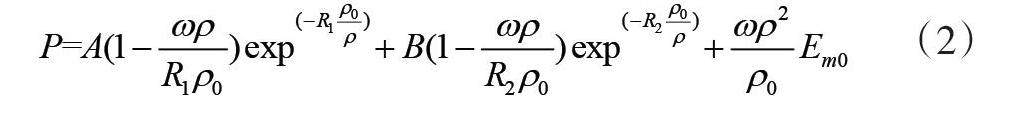
摘 要:为了评估多连拱形迎爆面对结构抗爆效果的影响,该文采用ABAQUS建立了具有等抗弯刚度的多连拱板形结构和单层平板结构的数值模型,利用耦合欧拉-拉格朗日算法(Coupled Eulerian-Lagrangian, CEL)对两种结构与空气冲击波之间的相互作用进行了研究,并对比了两种结构在化爆和核爆作用下的动力响应特性。在化爆作用下,和平板结构相比,多连拱形迎爆面能够改变爆炸冲击波的入射角及反/绕射路径,从而降低结构表面冲击波反射超压峰值、缩短正压持续时间、减小在x方向支座反力及底板中心点位移,因此能够显著削弱冲击波对结构的影响。然而,由于核爆冲击波会在结构表面快速形成持续稳定的空气高压区,后续爆炸冲击波相当于作用在空气高压区上,并且核爆炸冲击波会在相邻拱形面的连接处发生叠加,因此多连拱板形结构并不能起到明显的抗击核爆的作用。
关键词:多连拱形面 抗爆 CEL算法 动力响应
中图分类号:TD774 文献标识码:A 文章编号:1672-3791(2020)01(a)-0035-06
Abstract: In order to evaluate the effect of multi-arch surfaces on the structural anti-explosion performance, numerical models of the multi-arch plate structure and single-layer plate structure with equal bending stiffness were established by ABAQUS. Coupled eulnerian-Lagrangian (CEL) algorithm was applied to study the interaction between the structures and the air shock wave. In this work, the dynamic characteristics of the two structures under the action of chemical explosion and nuclear explosion were compared. In contrast to the flat plate structure, under chemical explosion, the incident angle and the reflection/diffraction path of the blast wave can be changed by the multi-arch surface, decreasing the overpressure peak of the surface shock wave, shortening the duration of positive pressure, reducing the support force in the x direction and the displacement of the center point. As a result, the impact of the shock wave on the structure can be weakened. However, when under nuclear explosion, a continuous and stable high pressure air zone around the multi-arch plate structure can be formed in a very short period of time. The subsequent incident blast wave was imposed on the surface of high pressure air zone. Moreover, the nuclear explosion shock wave tends to overlap at the junction of adjacent arch planes. Therefore, multi-arch plates can not significantly weaken the impact of nuclear explosion load on the structure.
Key Words: Multi-arch surfaces; Anti-explosion; Coupled Eulerian-Lagrangian; Dynamic response
文獻[1-3]研究表明,结构的迎爆面形状对结构的抗爆效果有较大影响。多连拱板形结构是一种上层为多连拱形结构、下层为平面板的双层结构。相关研究[4]表明,在受爆炸荷载冲击时,多连拱板形结构能够使所受到的力在相邻拱的连接处部分抵消,从而达到减小结构受力、提高抗爆能力的目的。因此,多连拱板形结构作为一种轻质的抗爆结构受到研究者们的广泛关注。Chen等[5]对多连拱板形结构在均匀脉冲荷载下的动力响应进行了研究。结果表明,当用钢量相等时,多连拱板形结构中拱形数量越多、拱形面越高、拱形层越厚,在均匀脉冲荷载作用下底板中心点的位移越小,结构越稳定。柳锦春等[6]对多连拱板形结构的力学性能进行了分析:当用钢量和起拱数量一定时,结构的抗力随着拱/板厚度比的增加呈先增加后减小的趋势;当多连拱板形结构为半圆拱,拱高与板的跨度比为0.07~0.1时,结构的抗力最大。但是,目前这些研究工作都是在保证用钢量相等的情况下进行的,并未保证2种结构的抗弯刚度相等。同时,现有文献也忽略了冲击波在相邻拱间可能存在叠加增强的作用,也没有系统对比多连拱形迎爆面对结构抗击化爆和核爆的不同影响。因此,该文采用ABAQUS建立了2种具有等抗弯刚度的多连拱板形结构和单层平板结构的数值模型,并利用耦合欧拉-拉格朗日算法(Coupled Eulerian-Lagrangian,CEL)对两种结构与空气冲击波之间的相互作用进行了研究,系统对比了2种结构在抗击化爆和核爆时的效果差异。与平板结构相比,多连拱形结构能够显著削弱化爆冲击波对结构的影响,但是并不能明显起到抗击核爆的作用。该文所得结果可以为多连拱板形结构的工程应用提供参考。
1 数值模拟设计
1.1 模拟设计思路
相关文献[7,8]表明,ABAQUS中的CEL算法能够有效地模拟爆炸荷载与结构之间的相互作用。因此,该文采用ABAQUS软件对多连拱板形结构和单层平板结构进行建模分析。具体数值模拟设计思路如下。
第一步,静荷载下等抗弯刚度设计。为了消除刚度的影响,对多连拱板形结构和单层平板结构采用静荷载下等抗弯刚度设计,即确保在底面作用相同静荷载时二者具有相同位移。
第二步,利用ABAQUS的CEL算法模拟化爆和核爆作用下2种结构的动态响应。在相同爆炸荷载下,以结构的变形和作用在结构上的峰值超压作为依据来评价结构承受爆炸荷载大小的能力。
1.2 静载下等抗弯刚度设计
该文中设计的多连拱板形结构尺寸如图1所示,为8节点的实体单元(C3D8R),模拟实验采用完全弹性材料(材料密度为7850kg/m3,弹性模量E为210GPa),底面荷载为3MPa(垂直于底面向下),两端固支。对该结构进行静载模拟实验,结果显示:当网格尺寸取10mm时,误差已经不超过2%,底板中点的位移为13.33mm。
为了对比,该文同时设计了平板结构,如图2所示。首先,平板结构的材料、长宽与多连拱板形结构的材料、长宽相等。然后,以两者在施加相同荷载(底面荷载为3 MPa,两端固支)的情况下具有近似相等的抗弯刚度(即底板中点位移相等)为依据,计算出平板的高度为41.5mm。
1.3 材料模型
在ABAQUS中,运用CEL算法模拟爆炸时需要使用本构模型和状态方程同时描述空气、炸药的特性。
根据文献[9],该文采用理想气体的状态方程模拟空气(*Eos,type=IDEALGAS),如式(1)所示:
P+P0=ρR(θ-θZ) (1)
式中,P为气体压强;P0为环境压强,初始值取标准大气压(1.01325×105Pa);ρ为气体密度,取1.297kg/m3;R为气体常数,取287.0J/(kg·K);θ为气体温度,初始温度设为288.4K;θZ为绝对温度的零值,取0K。另外,在具体分析时,需定义比热系数,为717.6J/kg·K。
炸药采用JWL状态方程描述(*Eos,type=JWL),如式(2)所示:
(2)
其中A、B、R1、R2和ω是材料常数;Em0为比内能,即单位质量物质所具有的内能;Vd为爆轰速度;ρ0为炸药初始密度,ρ为爆轰产物的密度。根据文献[10],该文中TNT的JWL参数如表1所示。
另外,空气和炸药采用欧拉单元(EC3D8R),網格为10 mm。
1.4 抗爆模型建立
多连拱板形结构的CEL算法模拟化爆的数值模型及模拟工况如图3所示。TNT当量取5kg,起爆点设置在炸药中心,位于底板中心正上方0.5m处。空气域的外部设置为无反射边界,采用关键字*CONTACT定义结构与空气的耦合关系。实体结构两端固支,材料模型与静载模型一样。平板结构的模拟工况与多连拱板形结构相同。
多连拱板形结构的CEL算法模拟核爆的数值模型及模拟工况如图4所示。材料性质用理想气体状态方程描述,网格大小为10mm。灰色区域为空气域,为1.2m×2 m×0.1m的立方体,采用欧拉网格。空气域四周采用对称边界,模拟无限大气环境。上表面设置为inflow-free欧拉边界,下表面设置为outflow-free欧拉边界。实体结构模型和约束同上,不作赘述。上表面作用核爆三角形衰减荷载(如图5所示:t=0时,超压为0.6MPa;t=300ms时,超压为0MPa),用以模拟入射爆炸冲击波。平板结构的模拟工况与多连拱板形结构相同。
2 结果与讨论
2.1 化爆荷载作用下多连拱形结构和平板结构动力响应特性对比分析
根据模拟,两种结构底板中点位移的时程曲线如图6所示。从图中可以看出,单层平板结构底板中点位移在3.9ms时就达到最大值(46.3mm),而多连拱板形结构底板中点位移在4.2ms时才达到最大(28.7mm),比单层平板结构减小了38.0%。多连拱板形结构在x方向的最大支座反力为1315kN,比单层平板结构的最大支座反力(1573kN)减小了约16.4%。以上结果表明,在化爆荷载冲击下,多连拱板形结构在x方向支座反力及底板中心点位移更小。这说明,多连拱形迎爆面有利于削弱化爆对结构的荷载,提高结构抗击化爆的能力。
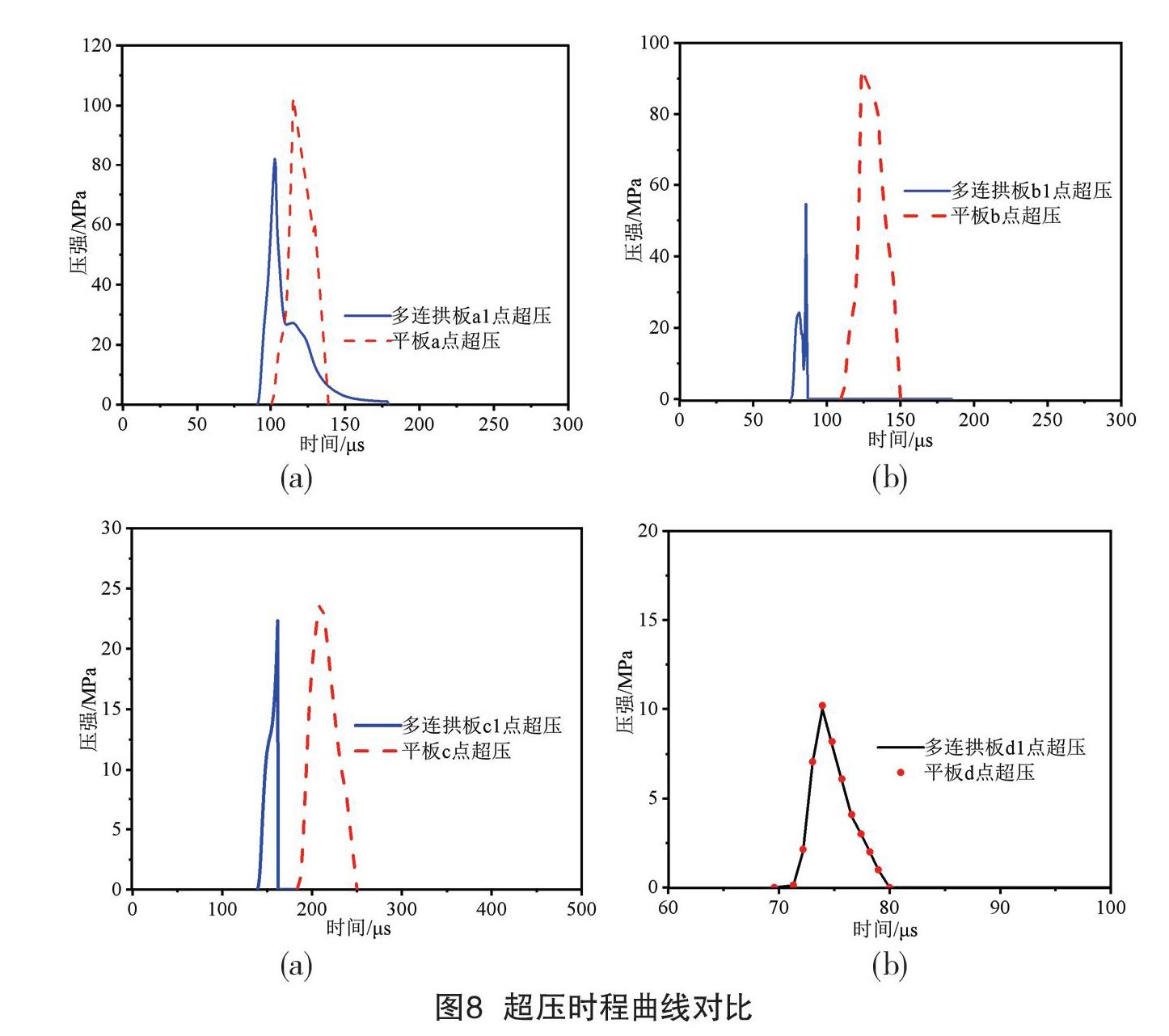
为了进一步分析多连拱板形迎爆面抗击化爆的作用机理,该文分析了爆炸冲击波在2种结构表面的超压云图(见图7)。从图7可以看出,多连拱形结构改变了爆炸冲击波的入射角,并且爆炸冲击波在多连拱形结构面上的反/绕射情况都不同于平板结构。图8为爆炸冲击波在各点的超压时程曲线对比。从图8可以看出,除d点之外(d点和d1点远离结构表面,它们的空气超压几乎相等),相比于平板结构,多连拱板形结构表面冲击波超压峰值更小、正压持续时间更短。例如:多连拱板结构b1点处超压峰值为54.6MPa、正压持续时间为10μs;平板结构b点处超压峰值为92.8MPa、正压持续时间为38μs;相比之下,多连拱板结构b1点处超压峰值减小了41%、正压持续时间缩短了73.7%。以上结果说明,多连拱形迎爆面能够减小化爆炸冲击波对结构的作用力,缩短作用时间,从而提高抗爆能力。
2.2 核爆荷载作用下多连拱形结构和平板结构动力响应特性对比分析
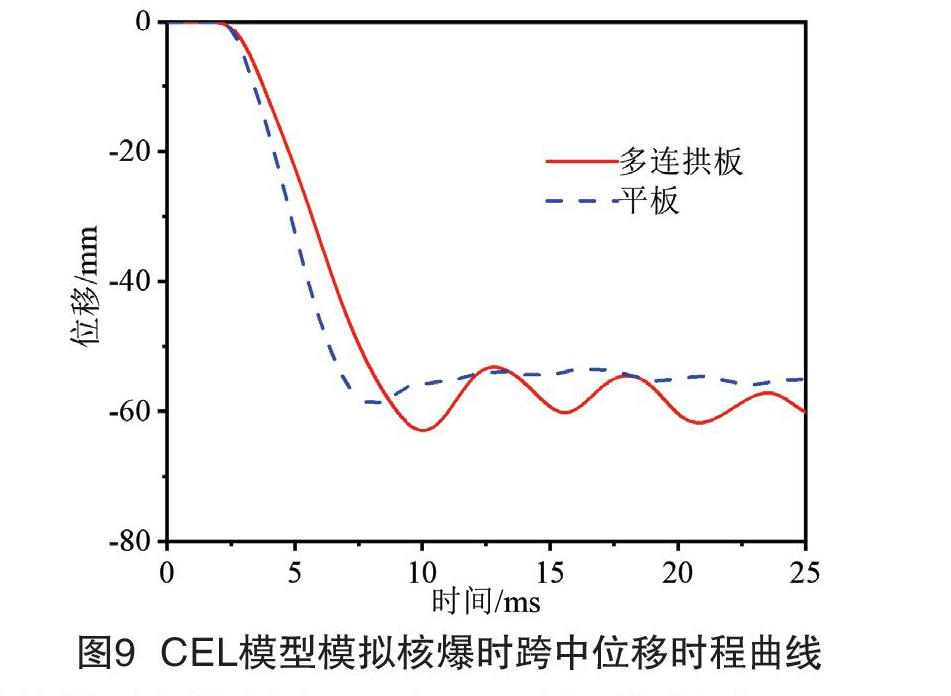
根据模拟,两种结构底板中点位移的时程曲线如图9所示。从图中可以看出:单层平板结构底板中点位移在8.0ms时达到最大值(58.7mm),而多连拱板结构底板中点位移在10.1ms时达到最大值(62.9mm),比单层平板结构的增加了7.2%;多连拱板形结构在x方向的最大支座反力为744kN,比单层平板结构的最大支座反力(946kN)减小了21.3%。
为了进一步分析多连拱板形结构对核爆荷载的影响,该文分析了核爆冲击波在两种结构表面关键点的超压时程曲线。其中,c点位于拱顶附近,a点位于两拱交点附近,b点位于拱形半圆45°附近,位置如图10所示。图11为多连拱板结构表面a、b、c点的空气超压时程曲线。从图11可以看到,当爆炸冲击波刚到达表面时,a点的超压峰值最大(5.5MPa),b点和c点的超压峰值较小(约4MPa)。这说明爆炸冲击波可能在a点附近发生了叠加增强,从而导致瞬时超压大于b点和c点。但是,随着时间的延长,3点的超压曲线很快趋于相同。通过对比单层平板结构和多连拱板结构在空间a点处的空气超压时程曲线(见图12)可以看出:在冲击波刚接触拱形面时,多连拱板结构模型a点处超压大于平板结构模型a点处空气超压,而在随后的极短时间内,两种结构在a点处的空气超压时程曲线基本趋于一致。图13为冲击波到达结构表面后,两种结构的冲击波超压云图。由此可以看出,由于核爆炸荷载持续时间较长,核爆炸冲击波到达结构表面后会迅速在结构附近形成空气高压区域,因此后续冲击波作用于空气高压区,而不是直接作用在结构面上,从而导致多连拱形结构并不能起到改变冲击波入射角的作用。
综合以上结果,我们可以得出如下结论:多连拱板形结构虽然能够减小结构在受核爆炸冲击荷载时x方向的支座反力,但是由于核爆炸冲击波能够在结构表面快速形成持续稳定的空气高压区,因此多连拱形结构改变冲击波入射角的作用消失,从而不能起到明显的抗击核爆的作用。反而,由于爆炸沖击波容易在相邻拱形面间的连接处发生叠加增强,从而导致多连拱板形结构的中点位移增加。
3 结语
为了分析等抗弯刚度下多连拱形结构的抗爆效果,本文利用ABAQUS软件建立了多连拱形结构和平板结构,模拟了两种结构在受到化爆和核爆冲击时的动态响应特性,得到以下结论。
(1)在相同化爆荷载作用下,多连拱形迎爆面能改变爆炸冲击波的入射角及反/绕射路径,并且降低表面冲击波超压峰值、缩短正压持续时间,从而减小在x方向支座反力及底板中心点位移。多连拱形迎爆面能够减小化爆冲击波对结构的影响,提高抗爆能力。
(2)由于核爆荷载持续时间较长、能在结构表面快速形成空气高压区,多连拱板结构虽然能够减小结构在受爆炸冲击荷载时x方向的支座反力,但是并不能明显削弱核爆荷载对结构的影响,反而会使爆炸冲击波在相邻拱形面连接处发生叠加增强。
参考文献
[1] 左清林.用数值方法对爆炸荷载下钢筋混凝土构件的动力性能的探索[D].上海交通大学,2009.
[2] 洪武,范华林,金丰年,等.刚性防爆墙迎爆面荷载计算方法研究[J].工程力学,2012,29(11):228-235.
[3] 庄立阳.爆炸荷载下曲形迎爆面防爆墙动态响应规律研究[D].北京建筑大学,2019.
[4] Chen W,Hao H.Numerical study of a new multi-arch double-layered blast-resistance door panel[J].International Journal of Impact Engineering,2012(43):16-28.
[5] Chen W,Hao H.Experimental investigations and numerical simulations of multi-arch double-layered panels under uniform impulsive loadings[J].International Journal of Impact Engineering,2014(63):140-157.
[6] 柳锦春.多连拱板结构的静动力学性能分析[A].第24届全国结构工程学术会议论文集(第Ⅱ册)[C].2015.
[7] 周天宇,张攀,程远胜,等.空中爆炸载荷下PVC泡沫夹芯板动态响应分析[J].舰船科学技术,2016,38(17):31-36.
[8] Rohit Tiwari,Tanusree Chakraborty,Vasant Matsagar. Dynamic Analysis of a Twin Tunnel in Soil Subjected to Internal Blast Loading[J].Indian Geotechnical Journal,2016,46(4):343-354.
[9] 艾森.大型整流罩分离仿真研究[D].大连理工大学,2015.
[10] Century Dynamics.AUTODYN theory manual, revision4.3[M].Concord,CA: Century Dynamics Inc, 2005.

