几类三角函数积分的方法总结

修风光

（沈阳理工大学理学院，辽宁 沈阳 110168）

1 借助三角函数之间的基本关系进行积分

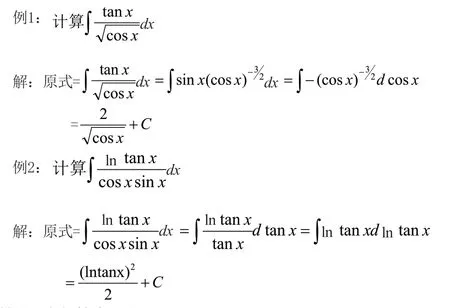
2 借助三角恒等式积分

六类三角函数之间除了基本的转换关系之外，还满足若干三角函数恒等式，例如

此外，正弦函数和余弦函数相关的和差化积、积化和差等等这些关系式在涉及三角函数的积分时，若能灵活运用，会大大简化积分的运算，从而达到积分的目的。

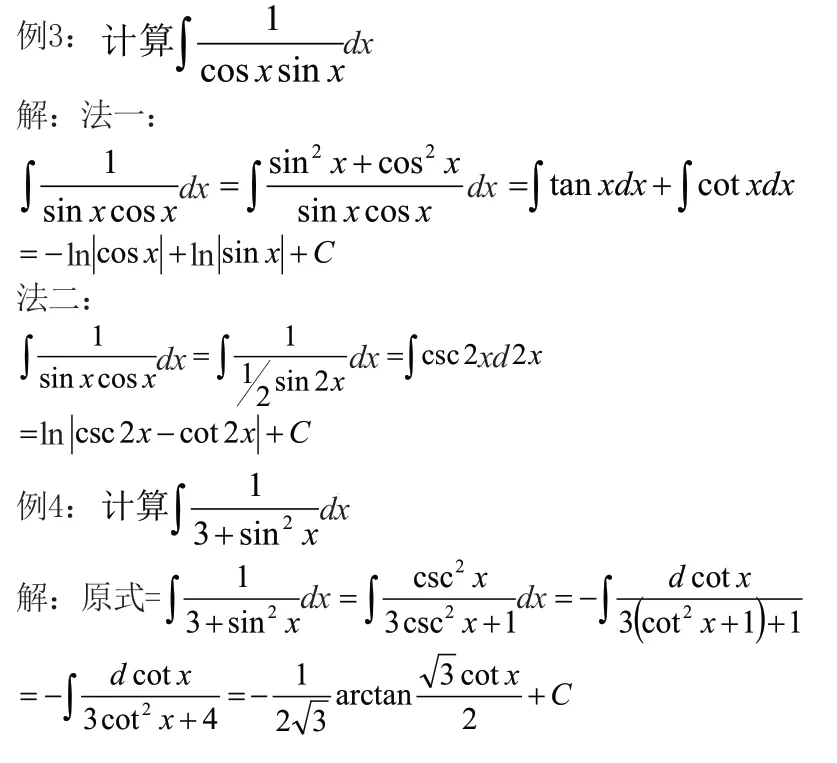
3 形如∫sin mxcosn xdx(m,n均 为非负整数)的不定积分

此时，可令xcos=µ，就可把上式转化为多项式的积分。

若n为奇数，则

同上，令xsin=µ，同样可转化为多项式的积分，然后借助基本积分公式正常积分即可。

若m,n均为偶数。则可借助相关的三角函数恒等式进行降次。当m,n数值比较大时，会需要多次降次，然后利用（1）和（2）的方法，借助第一类换元法进行积分。

4 形如∫secmxtann xdx(m,n均 为非负整数)的不定积分

1）若m为正偶数，则利用三角恒等式sec2x=tan2x+1有

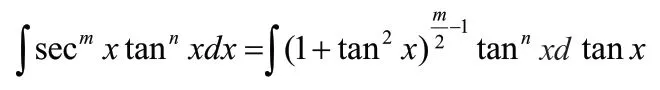
此时，可令xtan=µ，就可把上式转化为多项式的积分。

若m=0，则得积分此时

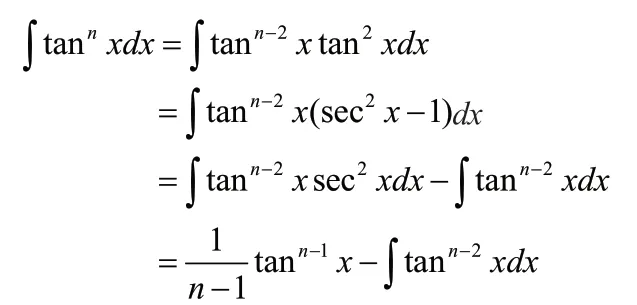
进而通过递推可得积分结果。

3）若m为奇数，n为偶数，则利用三角恒等式进行变形，进而可化为求形如的积分，然后借助分部积分法进行求解即可。

4）若m为奇数，n为奇数，则

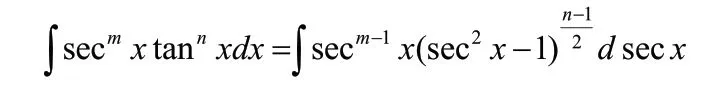
此时，可令xsec=µ，同样可转化为多项式的积分。

含有三角函数的不定积分处理方法往往不是唯一的，本文中所给出的方法经验证基本是最简便的。另外需要指出的是本文中提到的这些处理三角函数积分的方法是基于不定积分求解的一般方法。所以对于这些方法的掌握必须以熟练掌握基本积分方法为前提。同时一般高数教材中所总结的基本积分公式也应当熟记。这样多管齐下，才能快速准确地达到求解任何一个不定积分的目的。