电路分析中去受控源方法的探讨和应用

赵 娜 田艳芳 叶金凤

（湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002）

随着电子技术的飞速发展，含有受控源电路的分析在工程实际中占有很大的比例，因此，在电路学习过程中掌握含有受控源电路的分析方法十分重要。目前教科书中使用的分析方法是直接根据受控源的特点，利用基尔霍夫定律、戴维南定理和网络分析法进行分析求解，求解过程十分繁琐，并且计算中容易出错，是电路课程的难点。本文提出了一种新的解题方法——去受控源，即先把受控源等效为电阻或电压源与电阻的串联组合，将含有受控源的电路变成不含受控源的电路，再进行分析求解。

1 受控源的等效模型

由叠加定理和齐性性质可知，在线性电路中，任何一条支路的电压或电流与独立电源之间的关系为一次函数关系，任一支路间的电压或电流之间也表现为一定的线性关系。由于受控源的控制量一般为某一支路电压或电流，因此，可以将受控源代换成与独立电源存在一次函数的表示形式。

若设线性电路中某一受控源的端电压为Uk,其支路电流为Ik,则它们之间的关系可以写成Uk=Usk+Rk*Ik，其中Usk，Rk由电路参数决定，均为常数，这就是受控源的伏安关系。在受控源两端电压和流过它的电流保持不变的情况下，可以把伏安关系为Uk=Usk+Rk*Ik的受控源等效为一个电压等于Usk的独立电压源与阻值为Rk的电阻的串联组合，如图1所示。

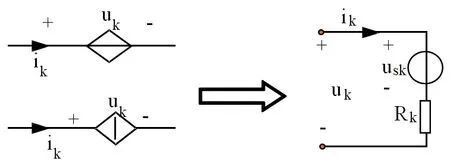
图1 受控源的等效模型

2 利用去受控源的方法进行等效应用

在含有受控源的电路中，受控源与它的控制量要么在同一条支路，要么在不同的支路，根据受控源支路与控制量支路所在的位置不同，其等效电路可分下面两种情况进行等效计算。

2.1 受控源的控制量和受控源在同一支路时

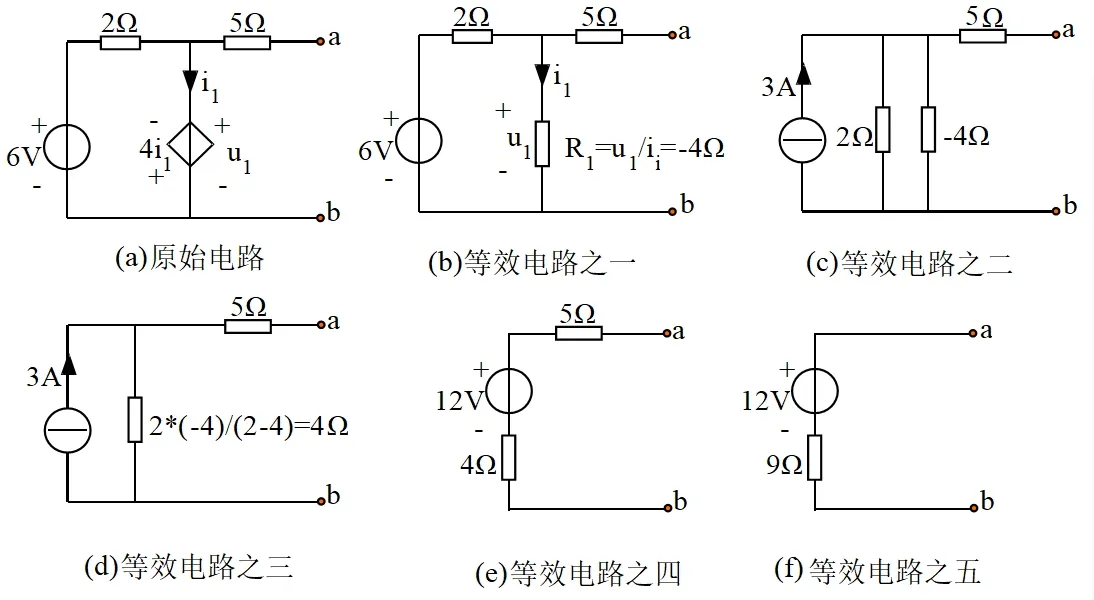
图2 例1求解过程

受控源的控制量和受控源在同一支路时，该受控源的端电压与电流之间成线性比例关系，即受控源表现为电阻性，受控源直接可用一只电阻等效替代，电阻大小为Rk=Uk/Ik。与普通电阻不同的是其阻值可能为负值，对外提供功率，只是该功率不是由本电路中的独立电源提供，而是由其它电源提供。等效之后，电路内不含受控源，对其分析求解就很容易。

例1：如图2(a)所示一端口网络为一有源器件的电路模型，求其戴维南等效电路。

2.2 受控源的控制量和受控源不在同一支路时

若受控源是受控电压源，首先找出控制量和受控电压源的电流之间的关系，再将受控源等效成电压源和电阻的串联组合形式，然后进一步求解。

例2电路如图3（a）所示，求一端口网络的等效电路。

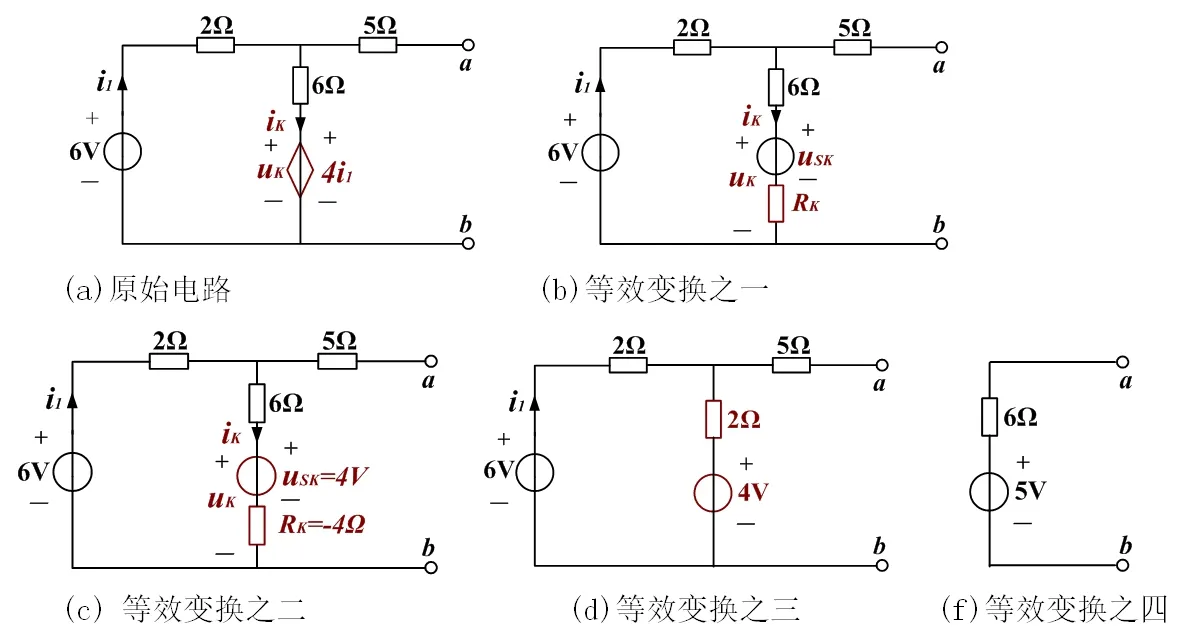
图3 例2求解过程

其中uK= 4i1，

对回路列写KVL方程： 2i1+6iK+ 4i1− 6 = 0得i1= 1−iK

则uK=4i1= 4 − 4iK即uSK=4V,RK=−4Ω

可见受控电压源可用Usk=4V的电压源与Rk=-4Ω的电阻串联来等效替代如图3(b)。等效替代后的网络不含受控源，如图3(c)。

若受控源是受控电流源，首先找出控制量和受控电压源的端电压之间的关系，再将受控源等效成电压源和电阻的串联组合形式，然后进一步求解。

3 结束语

由以上的电路分析可知，任何受控源都可以用一个等效电源或一个电阻替代，其等效的关键在于找出受控源的伏安关系。利用这种等效方法求解电路，可以避免复杂方程的列写和求解，是一种方便实用的解题方法。