数列综合应用“三剑客”
◇ 山东 李爱霞 梁桂媛
数列是高中数学的重要内容之一,也是历年高考考查的重点之一.特别是数列综合应用问题,往往还以解答题的形式出现,所以我们在复习时应给予重视.近几年高考数列的综合应用试题从数列的概念、等差数列和等比数列的基础知识、基本技能和基本思想方法入手,涉及函数、方程、不等式、解析几何、概率等知识的综合性试题,在解题过程中通常用到等价转化、分类讨论等数学思想方法,是属于中高档难度的题目.下面结合数列综合应用常见的“三剑客”加以实例剖析.
1 探究性问题
例1已知数列{a n}满足a1=1,a n·a n+1=a n-3a n+1.若.
(1)求数列{c n}的前n项和S n;
(2)试问:是否存在互不相同的正整数p,q,r,使S p,S q,S r成等差数列?若存在,求出p,q,r的最小值;若不存在,请说明理由.
解析

(2)若存在互不相同的正整数p,q,r,使S p,S q,S r成等差数列,不妨设p<q<r,则


等号两边同时除以3q,得

因为p,q,r∈N∗,且p<q<r,所以r-q∈N∗,r-q+p+1∈N∗,故式①等号左边3p+1+3r+1-2×3r-q+p+1+3r-q为整数,而p-q<0,所以3p-q∈(0,1),所以式①等号右边2-3p-r∈(1,2),所以不存在互不相同的正整数p,q,r,使Sp,Sq,Sr成等差数列.
点评
20世纪80年代以来,越来越多的摄影艺术家开始采用“设计”的方式进行创作。他们有意识地跟随广告业照亮的道路,运用想象与才智挣脱了古典现代主义的束缚。他们不是在现实世界中寻找主题,直接“拍摄”,而是选择自行“创造”一个全新的视觉世界。
数列中的探究性问题,往往以开放性与探索性等形式出现,此类问题以等差数列、等比数列等基本知识为基础,综合数列的定义、通项公式、求和公式,用来判断数列的类型、存在性问题,利用开放思维创新、探索思维拓展等加以考查与应用.
2 恒成立问题
例2已知λ<0,数列{an}满足an+1-λan=λ-λ2(n∈N∗),且a1=3λ.
(1)求证:数列{an-λ}是等比数列;
(2)若对任意的m,n∈N∗,都有恒成立,求实数λ的取值范围.
解析
(1)因为an+1-λan=λ-λ2,所以an+1-λ=λ(an-λ),因为a1=3λ,λ<0,所以a1-λ=2λ<0,从而an-λ≠0,所以,所以数列{an-λ}是首项为2λ、公比为λ的等比数列.
(2)由(1)知an-λ=2λ·λn-1,即an=2λn+λ,据题意知得-1<λ<0.当n=2k,k∈N∗时,a2k=2λ2k+λ>λ,故

当n=2k-1,k∈N∗时,a2k-1=2λ2k-1+λ<λ,故
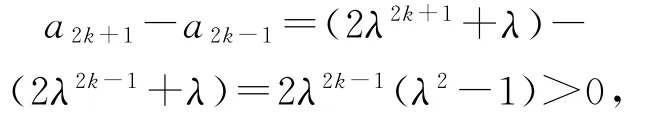
所以数列{a2k-1}单调递增;
因为对任意m,n∈N∗,都有,所以

且0>a2>a4>a6>…>a2k>…>λ,所以的最小值为所以.
综上所述,实数λ的取值范围是.
点评
数列恒成立问题能够很好地考查数列、函数、不等式等知识以及化归与转化等数学思想,因此备受命题者青睐,在复习时要有针对性地训练,从而灵活掌握与应用.加强这一类问题的训练有利于提高综合解题能力,在培养思维的灵活性、创造性等方面起到积极的作用.
3 创新定义问题
例3若无穷数列{an}满足:存在k∈N∗,对于任意的n≥n0(n0∈N∗),都有an+k-an=d(其中d为常数),则称{an}具有性质“P(k,n0,d)”.
(1)若{an}具有性质“P(3,2,0)”,且a2=3,a4=5,a6+a7+a8=18,求a3;
(2)若无穷数列{bn}是等差数列,无穷数列{cn}是公比为正数的等比数列,b1=c3=2,b3=c1=8,an=bn+cn,判断{an}是否具有性质“P(2,1,0)”,并说明理由.
解析
(1)因为{an}具有性质“P(3,2,0)”,所以an+3-an=0,n≥2,由a2=3,得a5=a8=3,由a4=5,得a7=5,因为a6+a7+a8=18,所以a6=10,即a3=10.
(2){an}不具有性质“P(2,1,0)”.
设等差数列{bn}的公差为d,由b1=2,b3=8,得2d=8-2=6,所以d=3,故bn=3n-1.设等比数列{cn}的公比为q,由c3=2,c1=8,得又q>0,所以所以an=3n-1+24-n,若{an}具有性质“P(2,1,0)”,则an+2-an=0,n≥1.
因为a2=9,a4=12,所以a2≠a4,故{an}不具有性质“P(2,1,0)”.
点评
数列创新定义的综合问题往往是在等差数列、等比数列的基础上加以类比、提升与拓展,解决此类问题往往需要将其转化为熟悉的等差数列、等比数列来分析与求解,实现创新能力与转化思维的统一,知识与能力的综合,达到创新目的.
由于数列是特殊的函数,而不等式是深刻认识与解析函数和数列的重要工具之一,三者的交会并以探究性、恒成立或创新定义等形式出现,是近年来高考命题的新热点.

