一道高中数学练习题的拓展与思考

◇ 贵州 柴玉辉

1 原题呈现

题目已知函数f(x)＝3x3＋2x.

(1)求f(2),f(－2),f(2)＋f(－2)的值;

(2)求f(a),f(－a),f(－a)＋f(a)的值.

【注:该题源自人教社A版高中数学《必修1》第一章第二节练习第2题】

解析

(1)f(2)＝3×23＋2×2＝28,f(－2)＝3×(－2)3＋2×(－2)＝－28,所以f(2)＋f(－2)＝0.

(2)f(a)＝3a3＋2a,f(－a)＝－3a3－2a,所以f(a)＋f(－a)＝0.

小结:因为函数f(x)＝3x3＋2x是定义在R上的奇函数,根据奇函数的性质易知:对于任意的x∈R,有f(x)＋f(－x)＝0.这是一个显而易见的结论.

2 对原题进行变式拓展

拓展1已知函数f(x)＝3x3＋2x＋1.

(1)求f(2),f(－2),f(2)＋f(－2)的值;

(2)求f(a),f(－a),f(－a)＋f(a)的值.

解析

(1)f(2)＝3×23＋2×2＋1＝29,f(－2)＝3×(－2)3＋2×(－2)＋1＝－27,所以f(2)＋f(－2)＝2.

(2)f(a)＝3a3＋2a＋1,f(－a)＝－3a3－2a＋1,所以f(a)＋f(－a)＝2.

拓展2已知函数f(x)＝3x3＋2x＋2.

(1)求f(2),f(－2),f(2)＋f(－2)的值;

(2)求f(a),f(－a),f(－a)＋f(a)的值.

解析

(1)f(2)＝3×23＋2×2＋2＝30,f(－2)＝3×(－2)3＋2×(－2)＋2＝－26,所以f(2)＋f(－2)＝4.

(2)f(a)＝3a3＋2a＋2,f(－a)＝－3a3－2a＋2,所以f(a)＋f(－a)＝4.

拓展3已知函数f(x)＝3x3＋2x＋m(m为常数).

(1)求f(2),f(－2),f(2)＋f(－2)的值;

(2)求f(a),f(－a),f(－a)＋f(a)的值.

解析

(1)f(2)＝3×23＋2×2＋m＝28＋m,f(－2)＝3×(－2)3＋2×(－2)＋m＝－28＋m,所以f(2)＋f(－2)＝2m.

(2)f(a)＝3a3＋2a＋m,f(－a)＝－3a3－2a＋m,所以f(a)＋f(－a)＝2m.

小结:由以上拓展1,2,3,易发现当f(x)的解析式由一个奇函数与一个常数的和构成,则在f(x)的定义域内,当自变量互为相反数时,函数值之和为2f(0),即为常数的2倍.

3 结论推广

结论若函数f(x)＝g(x)＋m满足g(x)为奇函数,m为常数,则在f(x)的定义域内,对于任意的a,有f(a)＋f(－a)＝2m.

证明由f(x)＝g(x)＋m且g(x)为奇函数可得

4 应用举例

例1已知函数f(x)＝x3＋sinx＋1(x∈R),若f(a)＝2,则f(－a)＝_______.

解析

令g(x)＝x3＋sinx,则g(x)为定义在R上的奇函数.

由上述结论有f(a)＋f(－a)＝2×1,所以f(－a)＝2×1－f(a)＝0.

例2已知函数若f(a)＝2,则f(－a)＝________.

解析

易求得函数f(x)的定义域为R,令g(x)＝则g(x)＋g(－x)＝0.所以f(a)＋f(－a)＝2×(－2)＝－4,故f(－a)＝－4－f(a)＝－6.

例3已知函数,则

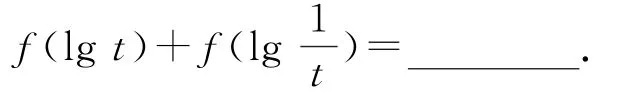
解析

教材中的例题或习题,都是经过若干专家和学者反复研究、精选出来的标杆,是专家学者的智慧结晶,对我们的学习、教学、高考备考等均有重要的示范、指导作用.