基于无梯度的分布式镜面下降算法
朱小梅,杨 婷
(重庆师范大学 数学科学学院,重庆 401331)
近年来,分布式优化算法、理论及应用受到了国内外学者的广泛关注[1-2].但现有的算法大部分都是针对分布式凸优化问题设计的,而在传感器网络、资源分配等问题中,经常会遇到目标函数是强凸的情形.因此,对强凸分布式算法进行研究是有意义的.现有分布式优化算法主要分为分布式次梯度算法、分布式对偶平均算法和分布式原始-对偶算法[3-5].分布式次梯度算法应用较为广泛,但该算法涉及到的梯度投影是基于Euclidean距离设计的,仅能处理一些具有简单约束的优化问题.将Euclidean距离推广到更一般的Bregman散度,Beck等[6]提出了一类分布式镜面下降(DMD)算法.该算法能有效处理高维约束优化问题,比如对具有单纯形约束的分布式优化问题,DMD算法能给出解析解.Yuan等[7]提出了一类分布式随机镜面下降算法用来求解强凸分布式优化问题,但该算法仅适用于无向网络,而对一般的有向网络[8-9]难以适用.
现有大多数分布式算法都是基于能直接获取目标函数的梯度信息来设计的,然而在许多实际应用中,梯度信息的获取往往十分困难或计算昂贵.因此,设计出一种无梯度计算的分布式算法是有价值和意义的.受文献[10-11]中利用函数值信息去估计难以获取原目标函数梯度信息的启发,本文提出了一种新的无梯度分布式镜面下降算法.不同于现有的DMD算法[6-7],本文提出的算法不需要目标函数的梯度信息,仅需要目标函数在两个随机点的函数值信息,进而克服了无法获取梯度信息的困难.同时,通过对算法的收敛性分析可以得到,本文所提算法的收敛速率是次线性的,与DMD算法具有相同的收敛速率.另外,本文设计的算法考虑的是时变有向网络,使其适用范围更加广泛.
1 预备知识
1.1 有向图
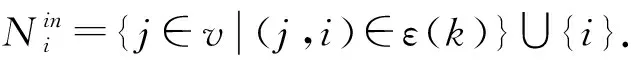
1.2 Bregman散度
定义1[6]1) 设函数h:m→是σh-强凸的,即满足对∀x,y∈m有:
h(x)≥h(y)+〈
(1)
2) 设函数h是σh-强凸并且是可微的,则由h定义的Bregman散度如下:
Dh(x,y)=h(x)-h(y)-〈h(y),x-y〉.
(2)
注1 ① Bregman散度具有一个重要的性质[6],即三点等式:
〈h(x)-h(y),w-x〉=Dh(w,y)-Dh(w,x)-Dh(x,y),∀w,x,y∈χ⊂m.
(3)
② 典型的Bregman散度有Euclidean距离与Kullback-Leiber(KL)散度[6].
1.3 函数光滑化
定义2[10]给定一个函数f(x):m→,对某个数δ>0,定义f(x)的一个光滑化近似函数:
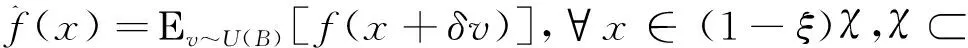
(4)
其中U(B)表示在单位球B={x∈m|‖x‖≤1}上服从的均匀分布,Ε[·]表示期望.对任意的x∈(1-ξ)χ,令梯度估计为:
(5)
其中u是单位球面S={x∈m|‖x‖=1}上的随机向量且服从均匀分布.
2 问题研究与算法设计
2.1 分布式优化问题
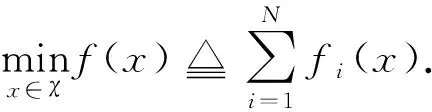
(6)
其中χ⊂m是一个公共约束集,每个节点i只知道自身的目标函数fi(x):m→.
假设1[8]时变有向图G(k)=(v,ε(k),P(k))满足:1) 图G(k)=(v,ε(k),P(k))是强连通的;2) 权重矩阵P(k)∈N×N是行随机的,即:且
假设2 1) 存在两个正常数r和R使得rB⊂χ⊂RB,这里B={x∈m|‖x‖≤1}表示单位球;2) 对任意的i∈v,fi(x)在χ上是L-Lipschitz连续的,即对任意的x,y∈χ,有|fi(x)-fi(y)|≤L‖x-y‖;3)fi是关于h的σf-强凸函数,即对∀x,y∈χ及∀i∈v有:
fi(x)≥fi(y)+〈fi(y),x-y〉+σfDh(x,y),
(7)
这里对某固定的x,Dh(x,y)关于第二个变量y是凸的[7].
2.2 无梯度分布式镜面下降算法
本文提出的无梯度分布式镜面下降算法包括以下步骤.
算法1 无梯度与布式镜面下降算法
第1步 初始化.设置总迭代次数K,步长参数ηk,压缩系数ξ,光滑化参数δ;对任意的i=1,2,…,N,设置k=1,初始点xi,1=0,wi,1=(0,…,1i,…,0).
第5步 令k:=k+1,转第2步.
注2 ① 与文献[6]提出的DMD算法相比,算法1不需要目标函数的梯度信息gi(yi,k)∈∂fi(yi,k),而是利用目标函数fi(·)在点yi,k附近的两个随机点yi,k±δui,k的函数值来近似估计梯度gi(yi,k),见第2步;② 算法1的设计基于不平衡有向图,第4步中wi,k+1的更新是为了减少有向图不平衡性的影响.
3 收敛性分析
首先给出两个重要引理,其中引理2给出了时变权重矩阵P(k)的性质,引理3给出了算法1的网络误差;然后给出了算法1的收敛性结果,见定理1.
引理2[8]如果假设1成立,考虑算法1,对任意的k≥l≥0定义P(k,l)=P(k-1)…P(l),且记[P(k,l)]ij为P(k,l)的第i行第j列的元素,定义P(k,k)=I,则存在一个归一化向量π(πT1n=1)使得:1) 对∀i,j∈v及∀k≥l≥0,存在常数α>0及β∈(0,1)有|[P(k,l)]ij-πj|≤αβk-l;2) |wii,k-πi|≤αβk;3) 对任意的k≥1和i∈v,存在一个正数ω使得ω≤wii,k≤1.
引理3 如果假设1、2成立,{xi,k}是由算法1产生的序列,则对∀i∈v,k≥1有:
(8)
证明根据算法1中第3步的xi,k+1的更新公式,使用一阶最优性条件可得:
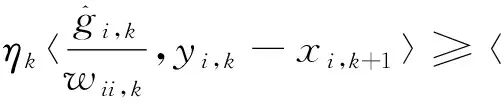
(9)
其中最后一个不等式由h的σh-强凸性可得.令ei,k=xi,k+1-yi,k,根据引理1和引理2可得:
(10)
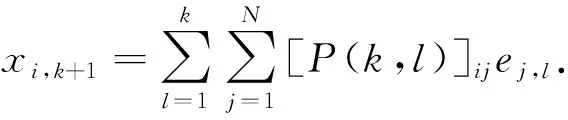

(11)
对式(11)两边取范数,并利用式(10)和引理2,即可得引理3的结果.
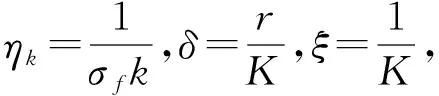
(12)
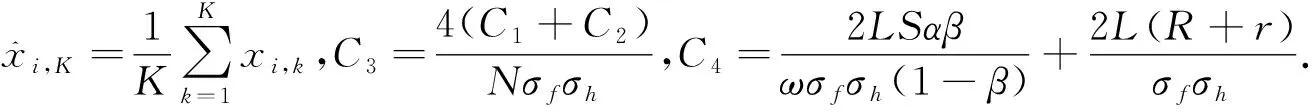
证明根据算法1中第3步的更新公式,使用一阶最优性条件可得:
〈h(xi,k+1)-
(13)
由式(3)及h的σh-强凸性可得:
〈h(xi,k+1)-h(yi,k),(1-ξ)x*-xi,k+1〉≤
(14)
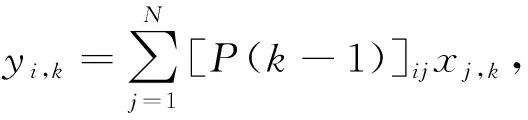
(15)
然后,在式(14)两边同时乘以πi并对i=1,2,…,N求和,可得:
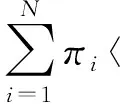
(16)
对于式(13),因为:
(17)
(18)
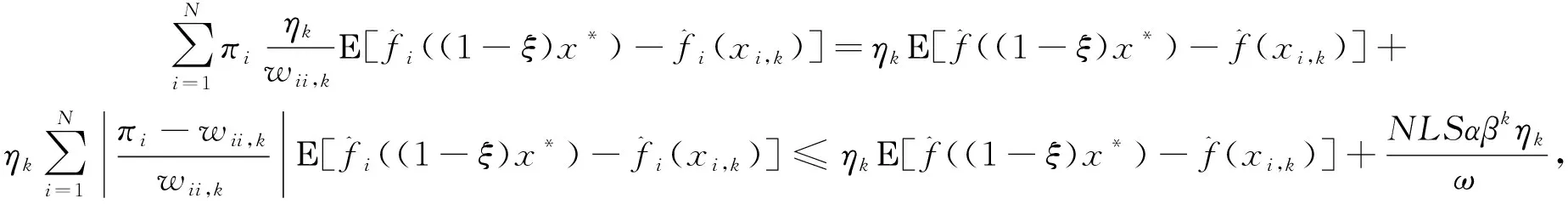
(19)
(20)
将式(20)代入式(17)并与式(16)结合,两边再对k=1,2,…,K求和可得:
(21)
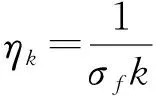
(22)
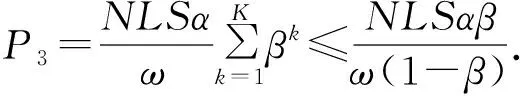
(23)
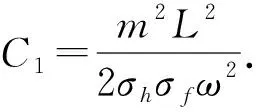
(24)
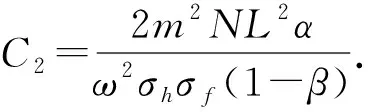
(25)
(26)
又因为:
(27)
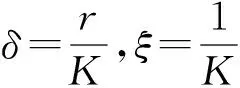
注3 ① 从定理1的结论可以得出:算法1的收敛率为O(ln(K)/K),与DMD算法的收敛率相同,但本文所提的算法1仅仅使用了计算量较小的函数值信息,而不需要梯度信息.算法1的优势在于节约计算成本,能处理梯度难以计算或获取困难的情形;② 算法1是基于时变的不平衡有向网络设计的,使其适用更一般的有向网络.
4 结语
针对一类梯度信息难以获取的分布式强凸优化问题,本文提出了一种无梯度的分布式镜面下降算法.该算法不需要梯度信息,但能够达到直接使用梯度信息相对应算法的收敛率.未来的工作考虑将该算法推广到分布式在线学习和非凸的分布式优化情形.

