定常Navier-Stokes方程的三个梯度-散度稳定化Taylor-Hood有限元

王炷霖， 敬璐如， 冯民富

(四川大学数学学院, 成都 610064)

1 引 言

Navier-Stokes方程(简称NS方程)是描述不可压缩流体运动的非线性偏微分方程.解NS方程的有限元法一直是计算数学领域的重要课题之一.

作为一个比较常用的有限元空间，Taylor-Hood有限元空间(简称TH元)采用连续的分片k次多项式空间作为速度逼近空间，连续的分片k-1次多项式空间作为压力逼近空间.文献[1-3]介绍了Scott-Vogelius有限元空间(简称SV元)，其速度逼近空间也采用连续的分片k次多项式空间，压力逼近空间则采用非连续的分片k-1次多项式空间.

在解不可压缩流问题时，TH元有比较广泛的应用.利用TH元虽能得到连续的速度及压力，但其离散速度解往往不满足质量守恒性质.文献[9-12]讨论了NS方程的带梯度-散度稳定项的有限元法，表明梯度-散度稳定项可以有效降低离散速度解的散度.此外，文献[13-14]证实当梯度-散度稳定项系数γ→∞时，梯度-散度稳定化TH元离散解逼近SV混合有限元离散解.

有限元法求解偏微分方程最终归结于解线性方程组.许多研究致力于发展有效求非线性NS方程有限元离散解的算法.其中，文献[15]介绍了求定常NS方程有限元离散解的迭代方法，并证明了在一定的强唯一性条件下某些迭代格式能够得到收敛到真解的离散解.文献[16-17]分别对比了三种求齐次和非齐次定常NS方程有限元离散解的迭代格式.受文献[13-14，16]启发，我们将文献[16]中求NS方程有限元离散解的迭代格式推广到梯度-散度稳定化迭代格式，用梯度-散度稳定项克服TH元解不满足质量守恒性质的问题.在强唯一性条件下，我们证明了这些梯度-散度稳定化TH元迭代格式的解在一定的迭代次数下逼近SV混合有限元离散解，且当梯度-散度稳定项系数γ→∞时TH元离散迭代解的散度趋于零.利用TH元求NS方程离散解时，相较于文献[16]中的三种迭代格式，本文提出的三种稳定化迭代格式的解能够更好的满足质量守恒性质.数值模拟验证了这一结论.

2 预备知识

考虑二维多边形区域Ω上的定常NS方程

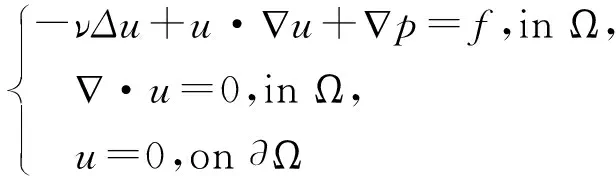
(1)

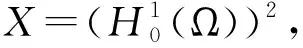
对X赋予范数‖v‖X=‖∇v‖.一般地，f∈X′的范数

众所周知，TH元取Ω上连续的分片k次多项式空间作为速度逼近空间，压力逼近空间则是取Ω上连续的k-1次分片多项式空间.SV元同样以Ω上连续的分片k次多项式空间作为速度逼近空间，其压力逼近空间也采用k-1次多项式空间，与TH元不同的地方仅在于SV元的压力逼近空间不要求在Ω上连续.当取特定网格剖分且选择合适的多项式次数时SV元是LBB稳定的，而TH元在以上情况下都是LBB稳定的.以下假设SV元与TH元是在特定网格剖分Λh下建立的LBB稳定的有限元空间.

定义TH元和SV元的速度有限元逼近空间为

vh=0 on ∂Ω}.

对TH元，定义其压力有限元逼近空间

定义SV元的压力有限元逼近空间

尽管TH元和SV元有相同的速度有限元逼近空间，但是它们的弱无散有限元子空间是不同的.定义

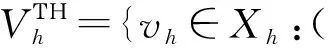
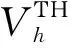
分别定义X×X,X×Q上的双线性形式

aγ(u,v)=(∇u,∇v)+γ(∇·u,∇·v),

∀(u,v)∈X×X，

b(v,q)=-(∇·v,q),∀(v,q)∈X×Q.

对TH元和SV元，都存在β>0，使得

(2)

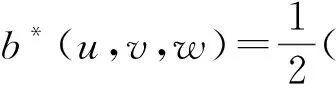
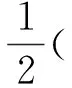
定义F(v)=(f,v),∀v∈X.

在后面的分析中需要用到以下引理.

引理2.1[16]存在只与Ω，h有关的常数CS，使得对uh,vh,wh∈Xh有

|b*(uh,vh,wh)|≤

CS‖∇uh‖·‖∇vh‖·‖∇wh‖

(3)

引理 2.2[14]∃M<∞，使得对任意rh∈Rh，

‖∇rh‖≤M‖∇·rh‖

(4)

下面我们研究四种求解定常NS方程的有限元.SV混合有限元法：

a0(uh,vh)+b*(uh,uh,vh)+

b(vh,ph)=F(vh),b(uh,qh)=0

(5)

梯度-散度稳定化TH元1：

(6)

梯度-散度稳定化TH元2：

(7)

梯度-散度稳定化TH元3：

(8)

(9)

在唯一性条件

CSν-2‖f‖-1<1

(10)

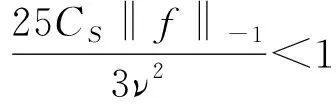
利用SV元，我们可以得到无散的离散速度解，但得到的离散压力解是不连续的.另一方面，利用TH元虽得到了连续的离散压力解，但离散速度解不是无散的.本节中我们将证明在γ→+∞时梯度-散度稳定化TH元1～3可以得到散度趋于零的离散速度解和连续的离散压力解，且梯度-散度稳定化TH元在强唯一性条件下随迭代次数增加逼近SV元解.

引理3.1设唯一性条件(10)成立.则对问题(5)的解uh有

‖∇uh‖≤ν-1‖f‖-1，∀n≥1

(11)

(12)

4CSν-2‖f‖-1<1

(13)

下有

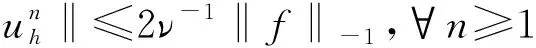
(14)

(15)

下有

(16)

证明 在问题(5)中取vh=uh有

ν‖∇uh‖2=(f,uh)≤‖f‖-1‖∇uh‖.

由Young不等式得

故

‖∇uh‖≤ν-1‖f‖-1.

同理可证式(12).

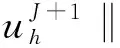
即式(14)成立.同理可证(16).证毕.

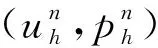
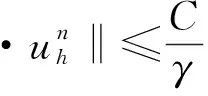
(17)

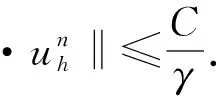
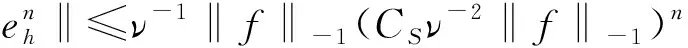
(18)

(19)

(20)

证明 由问题(5)(6)有

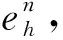
又由式(5)(9)知

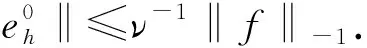
故式(18)成立.同理可得式(19).

又由式(16)知

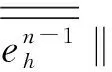
即

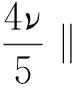
显然，当n=0时(20)式成立.假设n=J时(20)式成立.则由上式可得当n=J+1时(20)式成立.证毕.

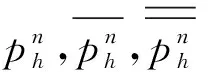
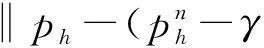
C‖f‖-1(CSν-2‖f‖-1)n

(21)

C‖f‖-1(3CSν-2‖f‖-1)n

(22)

(23)

证明 由问题(5)(6)有

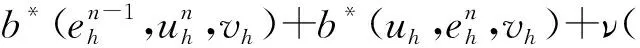
故

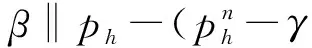
即(21)式成立.同理可证(22)(23)式成立.证毕.

4 数值算例

例4.1在问题(1)中取Ω=[0,1]×[0,1]，f及边界条件由二维定常NS方程的精确解确定.设精确解为

u1=10(x4-2x3+x2)(2y3-3y2+y),

u2=-10(y4-y3+y2)(2x3-3x2+x),

p=10(2x-1)(2y-1).

取k=2.采用图1所示10×10重心细分网格剖分.

图1 Ω上10×10重心细分的三角形划分

设(uh,ph)为问题(5)的解.表1，2给出了不同参数下梯度-散度稳定化迭代法1的计算结果，表3，4分别给出了ν=0.5时梯度-散度稳定化迭代法2及梯度-散度稳定化迭代法3的计算结果.

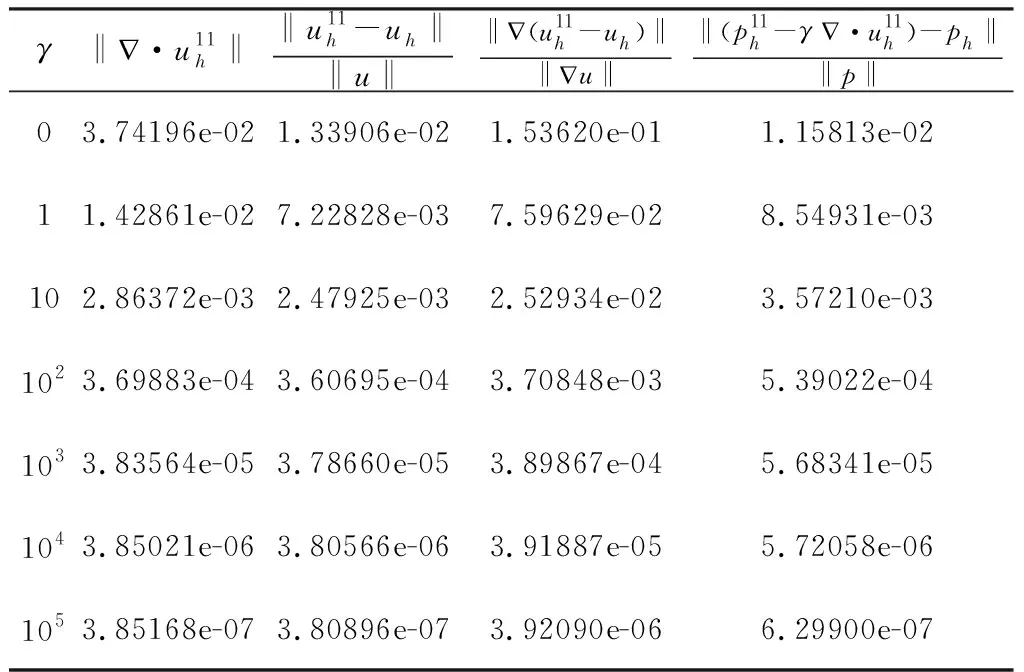
表1 ν=0.5时迭代法1的计算结果

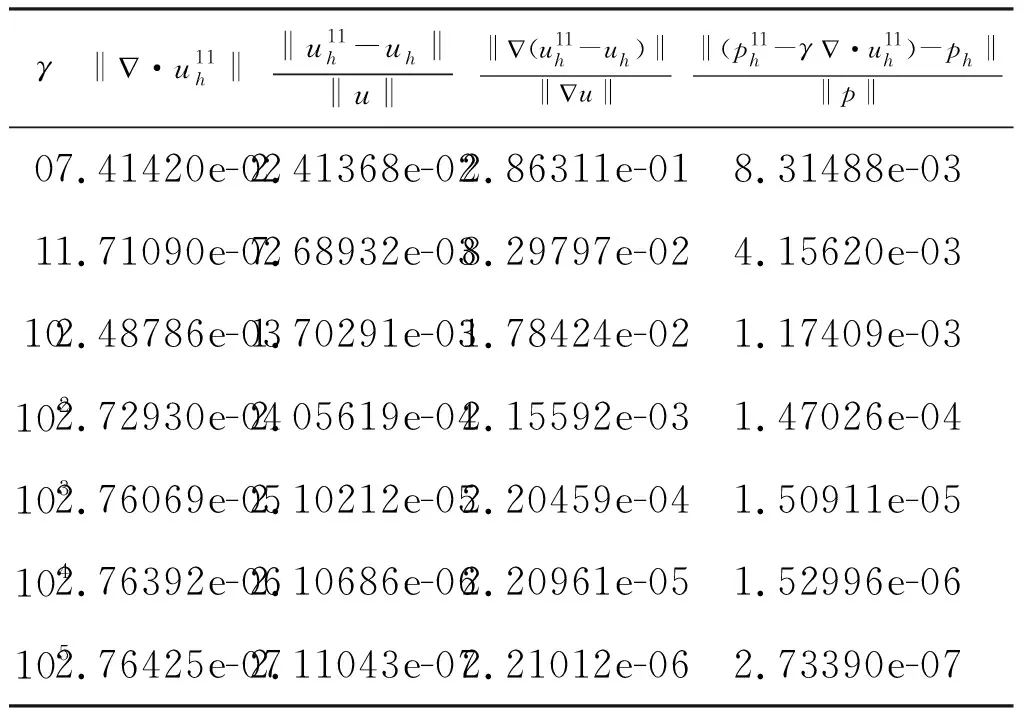
表2 ν=0.25时迭代法1的计算结果

表3 ν=0.5时迭代法2的计算结果

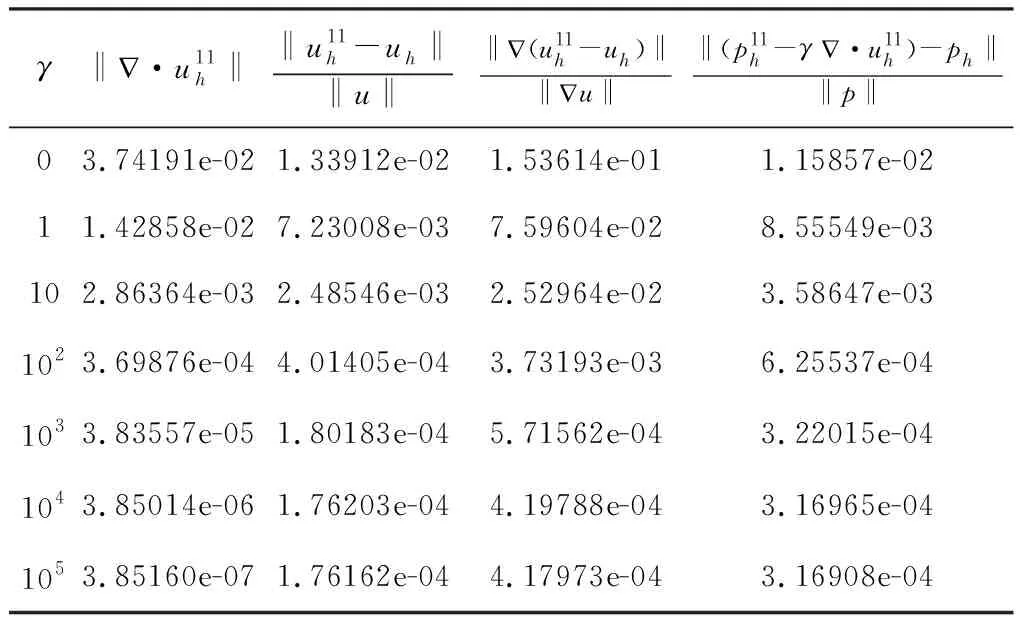
表4 ν=0.5时迭代法3的计算结果

计算结果显示，经过一定的迭代次数后，三种梯度-散度稳定化TH元迭代方法的解都可以很好的逼近SV混合有限元的离散解.通过增大梯度-散度稳定项系数，我们可以得到散度趋于零的离散速度解，且系数增大并不会造成TH元离散解与SV有限元离散解的误差增大.换句话说，通过在文献[16]中的三种迭代格式上加梯度-散度稳定项，利用TH元我们可以得到散度趋于零的离散速度解和连续的离散压力解.