基于天牛须和蝙蝠算法融合的PID参数整定仿真与研究
山石姣,马吉明,苏日建,温旭琴
(郑州轻工业大学 计算机与通信工程学院,郑州 450002)
近年来,随着学习算法和优化算法的不断深入发展,一些学者根据自然界生物的觅食等行为提出了很多种仿生群集智能优化算法.这一系列优化算法因为能够解决复杂优化问题,所以受到了当今人工智能研究领域的追捧[1].天牛须搜索算法[2-3](beetle antennae search algorithm,BAS)作为一种新型的单体智能优化算法,是由Jiang在2017年提出的.
天牛须搜索算法作为其中一种较新的优化智能算法,相对于遗传算法[4]、粒子群算法[5-6]等,BAS具有更大潜能,也被应用于多种优化问题,比如电力调度问题、神经网络、机器人、路径规划以及无人机等多个领域[7-14].基本BAS算法,虽然相比其他的群体智能算法,其运算量大大降低,但当迭代达到一定次数后,步长的锐减会导致天牛在各个方向上的移动分量过小,从而陷入局部最优后难以跳出.采用定步长可跳过最优点,混沌扰动可扩大搜索范围[15-18],但容易导致结果不稳定,并因为早熟收敛易陷入局部最优问题.
经过多次实验测试,本文将天牛须算法融入蝙蝠种群,在全局最优邻近进行加倍详细的局部搜索,以促进天牛种群进行寻优.同时,因为BAS的单一性,这种结合蝙蝠算法的方式也增加了BAS的丰富度.挑选6个经典测试函数,用Matlab进行仿真,将改进后的算法与传统的天牛须算法(BAS)仿真结果进行比较,结果显示,BAS-BA算法计算出的最优值总体上优于BA算法,从而证明了天牛须—蝙蝠混合算法(BAS-BA)能够较有效地避免BAS算法易陷入局部极值、收敛速度慢的问题.将BAS-BA用在优化PID的参数整定,得到参数值.并在离线的情况下与传统BAS对于PID的控制进行Simulink仿真对比,结果显示,BAS-BA方法优化的PID控制器没有超调现象,而BAS方法优化有超调现象.总体上看,基于BAS-BA优化系统调节能力比基于BAS优化系统优异.
1 天牛须—蝙蝠混合搜索算法
1.1 天牛须搜索算法(BAS)
基本的BAS主要步骤如下.
第1步:设定搜索公式,对随机生成的天牛的位置、天牛须的朝向进行描述,并进行归一化处理.
(1)
式中,d表示空间维度,rands(d,1)表示随机函数.
第2步:通过天牛触须的感知,进行向左和向右搜索,建立天牛的左须和右须以及质心的表达式.
(2)
(3)
式中,x为天牛的质心在第t(t=0,1,2,…,n)次迭代的位置,xri为天牛右须在第t次迭代的位置,xli为天牛左须在第t次迭代的位置,d0为天牛两个须之间第t次迭代的距离.
第3步:建立天牛的位置更新迭代模型.
(4)
(5)
etat=0.95×etat-1,
(6)
式中,eta为搜索的步长因子,f(x)为x位置的气味浓度,该函数为适应度函数,sign(.)为符号函数,返回参数的正负.式(5)和式(6)表示搜索参数d0和eta的更新规则.
1.2 蝙蝠算法(BA)
基本的蝙蝠算法(BA)[19-20]的主要步骤如下.
第1步:初始化种群位置为xi(i=1,2,3,…,N)和速度vi,搜寻目前蝙蝠群中最优蝙蝠位置为x*;并根据以下公式更新种群速度和位置.
fi=fmin+(fmax-fmin)α,
(7)
(8)
(9)
式中,fmax和fmin分别表示脉冲频率的最大值和最小值,fi为第i只蝙蝠的脉冲频率,α为随机数,在[0,1]上均匀分布.
第2步:随机生成一个数值R1,ri为第i只蝙蝠的脉冲频度,如果R1 第3步:生成一个随机数R2,如果R2 (10) (11) BA是基于迭代的优化算法,且在最优解周围通过随机飞行产生局部新解,加强了局部搜索.所以本文提出一种天牛须-蝙蝠混合算法(BAS-BA),解决BAS早熟收敛易陷入局部最优问题.BA种群中的每只蝙蝠都可以描述成天牛进行搜索,将BA算法最优解的随机游走思想融入天牛的位置更新过程中,可以增加天牛种群的多样性和位置多样性,增加了天牛搜索的丰富度.算法的具体过程描述如下. 第1步:初始化参数.种群的规模、范围,蝙蝠的响度、脉冲频率,天牛种群的初始步长.初始化种群的位置、速度. 第2步:初始化种群最优位置,在全局最优个体处进行局部寻优. 第3步:根据天牛群的位置更新公式(12)、(13)和公式(14)更新种群全局最优位置.根据蝙蝠种群位置更新公式改进的天牛群的位置更新公式如下: (12) (13) (14) 图1 BAS-BA算法流程Fig.1 BAS-BA algorithm flow chart 第4步:根据BA算法的第2步和第3步可知,蝙蝠通过在全局最优个体处发射脉冲信号产生局部解来实现局部最优搜索,再通过比较个体位置优劣,以及响度的大小来更新位置和新解.将该步骤融入新算法位置和最优值比较,同时,用BAS算法进行全局的最优搜索,引导天牛个体向全局最优位置处移动. 第5步:判断是否达到最大迭代次数、精度标准,若未满足则转向第2步. 算法流程图如图1所示. 为了验证改进的BAS-BA算法的性能,选取6个标准测试函数进行仿真测试.其中,f1是典型的二维测试函数;f2是一种典型的单模函数,可以测试算法的准确性;在有规律解的情况下,f3可以测试算法的实用性;f4函数振荡强烈并且难以获得全局最优解,可以很好地测试算法的性能;f5函数基本上是平坦的区域,由余弦波调制形成单独的孔或峰,难以用优化算法处理;f6函数是一个典型的非线性多模态函数,局部最小和搜索空间多,难以寻优.标准测试函数的公式如表1所示,测试函数均是非线性函数,理论最小值均为0.函数的搜索范围均为[-10,10]. 表1 测试函数Tab.1 Test functions 实验环境是在window10系统Matlab R2015a软件,CPU:i5-3470 3.20 GHz,RAM:4 GB. BAS-BA算法的参数设置:最大迭代次数Tmax设为100;种群大小N设为50;初始响度A设为0.25;响度衰减系数w设置为0.95;初始发射比率R设为0.75;发射比率增加系数r设为0.05;最大频率fmax和最小频率fmin分别为1和-1;天牛步长递减系数为0.95;须长率和初始步长分别为5和1.针对每一个函数,两个算法分别在搜索维度为2、10和30上独立运行30次,将计算结果进行对比分析,并分析算法性能. 图2 PID控制器系统框架图Fig.2 PID controller system diagram 图3 BAS-BA的PID参数整定控制Fig.3 PID parameter setting control diagram of BAS-BA 图4 Simulink环境搭建PID控制系统结构Fig.4 Construction of PID control system structure in Simulink environmen 2.2.1 PID控制原理 PID控制器[21]的原理图如图2所示.控制器由4部分组成:第一部分为r(t),表示期望值,即控制系统的目标信号;第二部分u(t)为控制器的输出,控制公式如式(15)所示,在整个系统中起到关键作用;第三部分为具体问题中的被控对象;第四个部分y(t)表示实际输出的结果,为控制系统最终得到的响应结果. 控制方程为: (15) 式中,e(t)=r(t)-y(t)代表控制偏差,Kp、Ki、Kd为与之组成的系数,通过公式(15)中3个系数与偏差的组成形式,将Kp叫作比例系数,Ki叫作积分系数,Kd叫作微分系数.偏差和相应的系数Kp、Ki、Kd组成了它的3个重要环节,这3个系数的不同组合会影响控制系统响应的性能指标的值,所以Kp、Ki、Kd这3个系数的优化是PID控制的关键[22-23]. 2.2.2 PID参数整定的基本思想 利用BAS-BA寻优和整定PID控制器的3个参数:算法每次迭代后,得到更新的位置信息,然后将位置上的3个维度的分解量分别赋值给Kp、Ki和Kd.并在Simulink环境中,对PID系统进行仿真,最后将系统产生的误差代入到适应度函数中,然后计算其适应度值.将获得的适应度值传递到BAS-BA中,与设定的阈值进行比较,得到PID的最优参数.系统框图如图3所示. 2.2.3 仿真设计 利用Matlab的Simulink环境搭建PID控制系统.利用BAS-BA不断调用PID控制器模型,进而用算法迭代得到最优的PID参数.并与BAS算法得到的PID参数进行对比. BAS和BAS-BA算法的参数调整为:维度设置为3;天牛两个须的距离为2;初始步长step设置为2;搜索范围为[0,1].BAS-BA其他参数不变. 选取的被控对象的传递函数为: (16) 适应度函数选择误差性能指标ITAE: (17) Simulink环境搭建PID控制系统结构图如图4所示:图中上半部分为BAS-BA算法中的ITAE性能指标的值;下半部分为PID控制结构. 将f1~f6函数在两个算法运行下所得平均值、最差值、最优值和方差作为算法精度和鲁棒性的衡量指标,测试函数在2维和20维的运行结果如表2、表3中数据所示,为了多角度分析结果,选取10维的进化曲线进行对比.图5中横轴为迭代次数,纵轴为最优适应度值.进化曲线如图5所示. 表2 搜索维度为2维时6个函数的性能比较 表3 搜索维度为20维时6个函数的性能比较 表4 参数值Tab.4 Parameter values (a) Booth function函数 (b) Sphere函数 (c) Rastrigin函数 (d) Salomon函数 (e) Griewank函数 (f) Ackley函数图5 搜索函数为10维时各个函数的进化曲线Fig.5 Evolution curve of each function when the search functions are 10 dimensions 从表2、表3和图5可以看出,当测试函数在2维、10维和20维时,BAS-BA算法总体上比BAS算法的精度更高、鲁棒性更好.BAS-BA算法解决了BA算法在多维运算上的劣势,又丰富了BA算法的丰富度.虽然BA算法本身的优势是单体智能,使得运算量降低,运算速度快,但是精确度不高,容易陷入局部最优,BAS-BA有效地避免了这些缺点. BAS与BAS-BA算法得到的PID中三个参数的迭代变化趋势以及得到的最优个体适应度值如图6-7所示.为了验证基于BAS-BA的PID参数整定的优良效果,将BAS和BAS-BA算法应用于PID控制器的结果进行对比,其参数和性能如表4所示,可以明显地看出BAS-BA计算出的性能指标优于BAS计算出的性能指标. 图6 BAS算法优化参数值及适应度曲线Fig.6 BAS algorithm optimization parameter values and fitness curves 图7 BAS-BA算法优化参数值以及适应度曲线Fig.7 BAS-BA algorithm optimization parameter values and fitness curves 从图8和图9的PID阶跃响应曲线可以看出,BAS优化和BAS-BA优化方法得到的PID控制器达到系统设定值的时间差不多,但BAS优化方法存在超调现象.综合比较,使用BAS-BA方法优化的PID控制系统调节能力比基于BAS优化方法的优异,具有良好的控制性能. 图8 BAS优化的PID控制器阶跃响应曲线图9 BAS-BA优化的PID控制器阶跃响应曲线Fig.8 BAS optimized PID controller step response curve Fig.9 BAS-BA optimized PID controller step response curve 本文提出了天牛须蝙蝠融合算法(BAS-BA),解决了天牛须搜索算法(BAS)出现收敛速度慢、精度低、易因为早熟收敛陷入局部最优等问题,使得算法能快速地寻找到更优的位置,从而加快了收敛速率.运用6个基本测试函数分别在2维、10维、20维进行对比实验,验证了BAS-BA算法相比于传统的BAS算法的收敛速度和鲁棒性更优.最后用BAS-BA算法优化PID控制器参数,通过与BAS算法得到的仿真结果进行对比,实验数据表明,BAS-BA算法得到的PID三个参数的性能指标明显优于BAS算法得到的结果.下一步工作将考虑群体智能技术应用于微型软体机器人运动控制的其它环节、大数据降维等相关多目标[24]求解及优化问题中.1.3 天牛须-蝙蝠混合算法(BAS-BA)

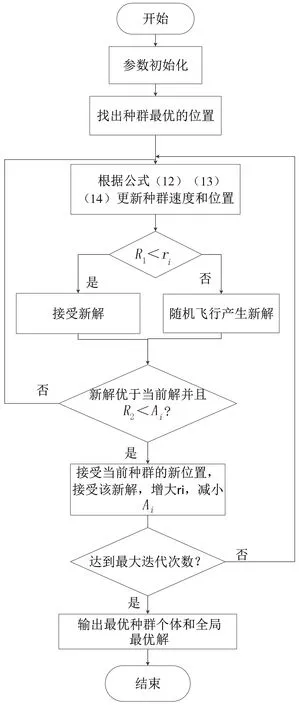
2 实验仿真设计
2.1 测试函数及测试环境




2.2 基于BAS-BA的PID参数整定仿真模型

3 仿真结果与分析
3.1 测试函数实验分析



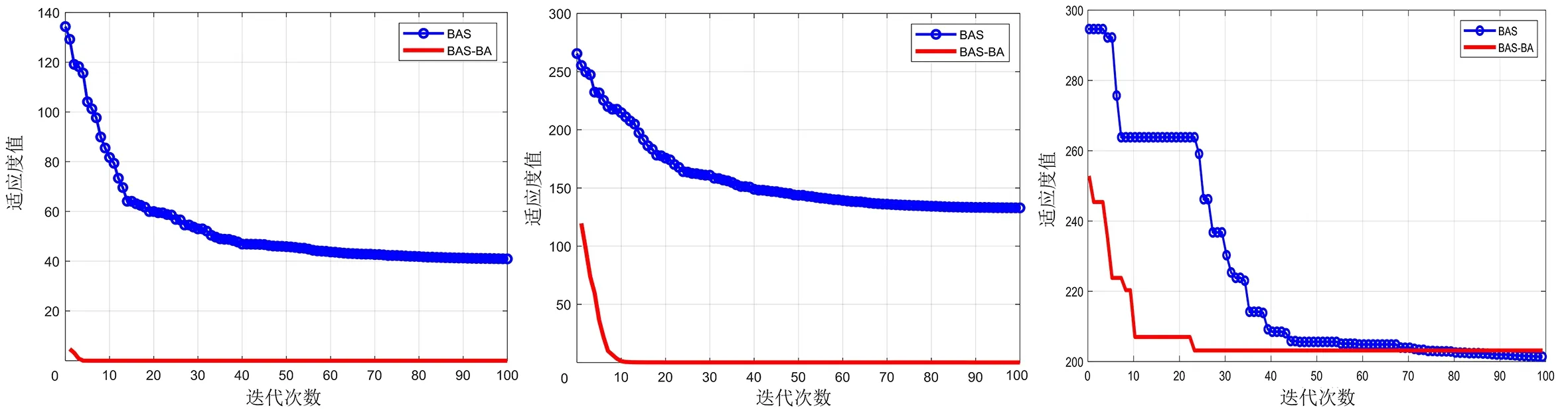

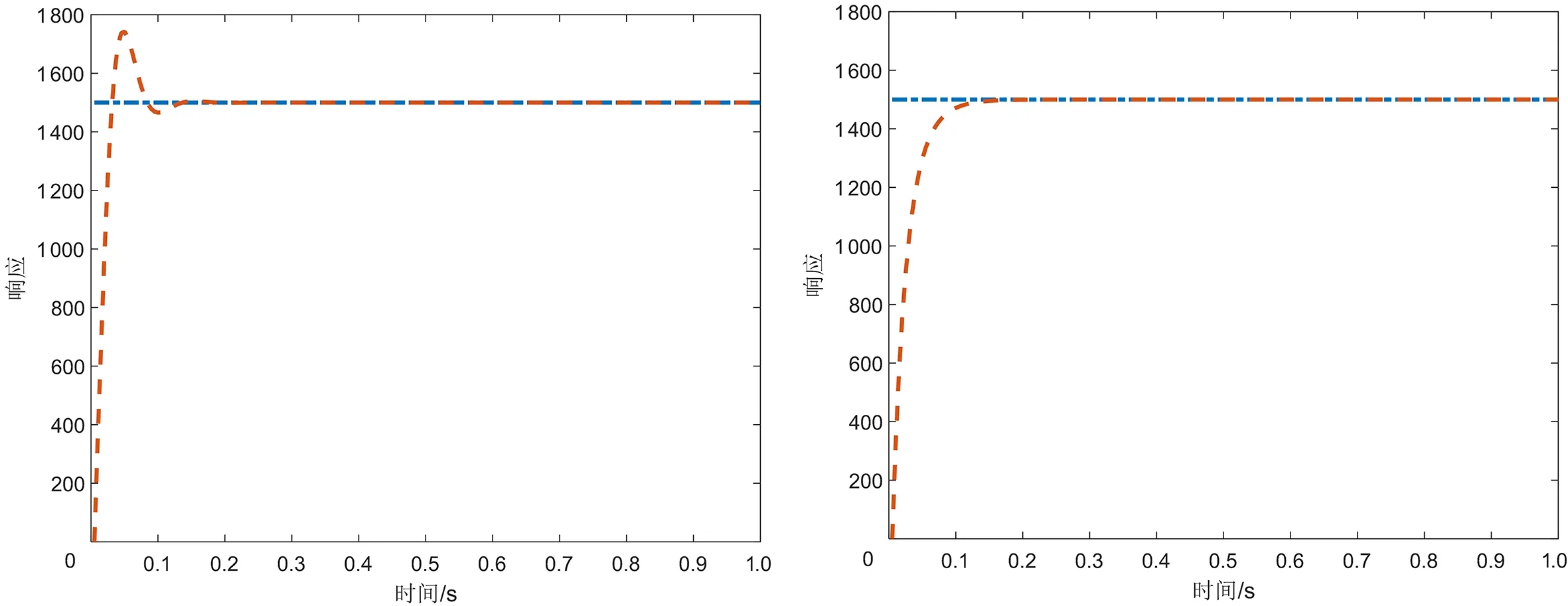
3.2 BAS与BAS-BA算法仿真对比分析
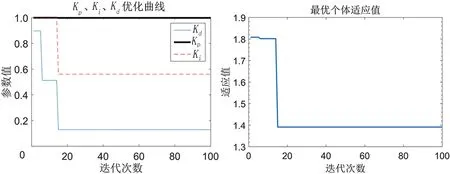
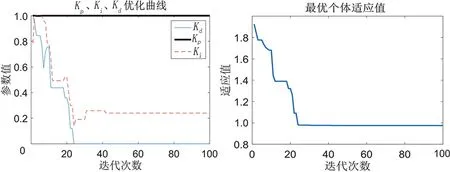
4 结论

