问题驱动教学

江苏省南京市第九中学 张 冉

近日，笔者有幸面向本区展示了《抛物线及其标准方程》这节公开课。本文是笔者对这节课的再整理及再思考。

一、教学过程简录

1.情境引入，提出问题

师：最近我们研究了具有某种几何特征的动点轨迹。如：椭圆是到两定点的距离之和为定值的点的轨迹；双曲线是到定点的距离之差的绝对值为定值的点的轨迹。请确定满足下列条件的点P的轨迹：

给定直线l和直线外一点F，过直线上任一点G作l的垂线，交线段FG的垂直平分线于点P，点G在直线上变化，得到动点P的轨迹。（如下图）

问题1：动点P具有怎样的几何特征？

生：P点是垂直平分线上的点，所以PF=PG。

师：P还是l垂线上的点，则PG的几何意义是？

生：PG表示P到定直线l的距离。

师：总结来说，动点P的几何特征是？

生：P到F的距离等于到直线l的距离。

【设计意图】借助情境中的垂直平分线条件，找到动点P的几何特征是PF=PG，即P到定点F和到定直线l的距离相等。否定轨迹为椭圆或双曲线，并为给出抛物线的定义和探究P点的轨迹方程做铺垫。

问题2：动点P的轨迹是何曲线？

师：图形直观显示，P的轨迹像是椭圆或者双曲线的一部分。思考动点P的轨迹是什么曲线？椭圆？双曲线？

生：都不是。因为动点P不满足以上两种圆锥曲线的定义，P的轨迹应该是其他的曲线。

师：华罗庚曾说“数缺形时少直观，形缺数时难入微”。我们要想严谨地判别出P的轨迹，单纯依靠图形是不够的，还需要借助代数手段，也就是探究P点的轨迹方程。

【设计意图】明确了P点的几何特征之后，结合给出的轨迹形状，学生有了直观的认识，然后探究P点的轨迹方程。

2.合作探究，体验过程

明确研究轨迹方程的一般步骤后，对坐标系的建法进行引导探究。学生在三种坐标系下分别求出抛物线的方程，并通过自主比较得出以抛物线顶点为坐标原点，对称轴为坐标轴的建系条件下得到的方程最为简洁，称为标准方程。

3.自主建构，归纳概括

师：回到问题2，刚才从形状上不能判别是否为椭圆或双曲线。现有了轨迹方程，请从方程结构入手，分析是何曲线？

生：不是椭圆，也不是双曲线，椭圆与双曲线的方程中，x、y的最高次项都为2，而此方程中x的最高次项为1，y的最高次项为2。

师：那你认为是何曲线呢？

师：我们是否学习过这样的表达式：一个变量的最高次项为2，另一个变量的最高次项为1？

生：一元二次函数。

师：该方程可以看作是x关于y的一元二次函数表达式吗？

生：可以，那么P的轨迹为抛物线。

【设计意图】新知旧知结合。

师：请结合P的几何特征，给出抛物线的定义。

生：到定点和到定直线距离相等的动点P的轨迹是抛物线。

师：在该定义中，将定点F称为焦点，定直线l称为准线。

师：椭圆定义中要求定量间满足2a>F1F2。这里给的定点定线间是否有补充说明？

生：定点不在定直线上，否则P的轨迹为过F点的垂线。

师：很好。由此得到：到定点F和到定直线l（F不在l上）上的P的轨迹为抛物线。

4.深化巩固，拓展延伸

引导学生得到抛物线的其他三种标准方程，并从焦点所处坐标轴、正负半轴角度区分四种标准方程，将图像与方程相结合。

二、对教学设计的再思考

情境引入中，学生可得到PF=PG，但不能将PG理解为动点到定直线的距离，即使在引导后认识到动点P到F的距离等于到直线l的距离，仍没有体会到要寻找动点和定量之间的关系。其实设置该问题情境的目的是揭示抛物线的形成是由到定点和到定直线的距离相等的动点构成，而该情景的主要难点在于表述和提炼这一关系，模糊了主题。

结合两节课的情况，笔者取两种概念给定方式的长处，从特殊到一般，由浅入深地探究抛物线的定义。以下是优化后的方案：

问题1：已知动点P（x，y）到点A（0,1）和到直线y=-1 的距离相等，求点P的轨迹方程。

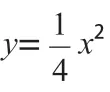
【设计意图】由具体的抛物线方程入手，与一元二次函数图像相结合，将教学内容纳入学生的知识结构中。

师：初中即学过一元二次函数的图像是抛物线，今天我们通过绘制到定点A和到定直线l距离相等的点的轨迹也得到了抛物线，这是巧合吗？会不会是抛物线的又一形成方式呢？

师：一元二次函数的图像是开口向上或向下的抛物线。接下来，我们借助几何画板绘制开口方向更为一般的抛物线。

活动一：直尺、绳索画抛物线的视频展示。

活动二：几何画板展示。

【设计意图】通过画抛物线的形式，给学生观察、归纳、组织数学语言的机会，让教学与学生发展相适应。

问题2：请根据绘制过程，给出抛物线的定义。

生：到定点和到定直线距离相等的动点P的轨迹是抛物线。

三、教学感悟

“问题是数学的心脏”，思维是由问题开始的，有了问题才有思考。问题情境的创设对于学生数学概念的理解渗透至关重要，教学中应着力创设有利于培养学生数学核心素养的问题情境。如何提高数学问题情境的有效性，需要我们立足课堂，在课堂教学中开展对话交流，产生思维碰撞，进而看清问题的结构，这样才能更好地理解问题及相关数学概念的本质特征。