“三 思”

李旭

【摘要】关注思考过程、数学思想、思维素养能促进形成有效的评价体系和模式.“三思”的有效评价，具有针对性、指导性、启发性，不仅仅关注学生学习的结果，还关注学生学习的过程;不仅仅展现学生的思维过程，还培养核心素养.

【关键词】思考过程;数学思想;思维素养;有效评价;核心素养

【基金项目】本文系福建省教育科学“十三五”规划2018年度教育教学改革专项课题《构建“3+1”数学尚思课堂的行动研究》（编号Fjjgzx18-25）的成果.

《义务教育数学课程标准（2011年版）》指出：“學习评价的主要目的是全面了解学生数学学习的过程和结果，激励学生学习，改进教师教学.”因此，有效的评价不仅仅关注学生学习的结果，同时也要关注学生的学习过程.有效的评价还应当展现学生的思维过程和培养核心素养.那么，如何才能达到有效评价呢？笔者认为在设计评价练习时，教师应该积极从以下三个方面进行思考.

一、体现思考过程——促进评价的针对性

传统的评价练习基本都是考查学生的学习结果，较少重视评价学生思考的过程.答案正确仅仅代表结果，学生或许是走了很大的弯路，或许对过程一知半解，或许甚至是猜测得到的结果.而答案错误仅仅代表结果，或许学生思考得更多，或许仅仅是最后一步出错，或许运用的方法或思考方式值得赞赏.教师只有重视过程的评价练习，才能全面评价学生的学习，才能看透学生的思考过程，才能暴露出学生的思路和理解的错误和问题，得知学生理解的薄弱环节，进而对症下药，进行有针对性的巩固和提升.

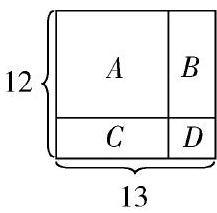
例如，教师在对两位数乘两位数进行评价的时候，可以出这样的问题来考查学生对算理理解的思考过程：图中哪个长方形代表13×12=？学生首先要明白这个长方形长13分成两部分，长的是10，短的是3，长方形宽12分成两部分，长的是10，短的是2.这样对每一个长方形面积的意义，以及所对应的乘法算式有了从直观到本质的了解.而根据算理的理解，计算过程中的“1×2”表示的是10×2，对应长方形的面积即为C.学生通过辨析和选择，对图形的分析，联系乘法算理，明确计算过程的本质含义，充分展示了思考的过程，不仅提升了针对计算进行算理的考查，还提升了数形结合、数感、应用意识等数学核心素养.

又如，三年级会遇到类似15×15○16×14 ，99×99 ○101×97比大小的问题时，不妨设计体现思考过程的评价练习，在注重过程的思考和推理的同时，发现规律：

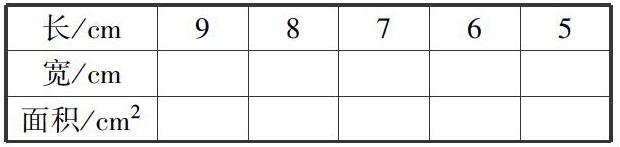
（1）周长20 cm的长方形，如果长和宽都是整数，完成下表.

我发现：周长一定的长方形，长和宽差距越，面积就越.

（2）你能快速比较下面的大小吗？说说理由.

15×15○16×14  99×99○101×97

学生通过列表探究，充分经历探究的过程，通过思考，发现规律，进而解决问题，这样的评价才是针对学生的知识盲区进行形象的、真实的、扎实的训练，进而促进学生对该类型比大小问题的本质理解，从而提升能力.

再如，在五年级下册学习了分数基本性质后，我们可以设计以下的练习来评价学生学习分数基本性质的思考过程：下列无法得到与ba大小相等的分数是（   ）.

A.b×2a×2  B. b÷0.5a÷0.5  C.b+3ba+3a  D. b-3ca-3c

对于本题，学生应该根据分数的基本性质的结论很快确定A和B的正确性，而重点就是评价学生的学习过程，因此C，D两个选项才是考查的重点.C可以借助乘法分配律转化成b×4a×4，这样的思考过程将分数的基本性质进行变式或者是迁移，进而更全面地理解和掌握分数的基本性质.虽然D和C的表达结果很像，但是认真观察会发现分子分母都是减去3c，相当于减去同一个数，不符合分数的基本性质.该题考查评价分数基本性质的运用及变式，重点分析和区别各种思考的过程，提升分数基本性质的拓展使用能力.这样的评价剖析了学生思考的过程，通过过程的观察、对比、分析、总结，积累了活动经验，丰富了分数基本性质的表象，培养了学生数感和推理能力等数学核心素养.

二、体现数学思想——增强评价的指导性

现代化的学生观表明学生是发展性的人.[1]课标“四基”强调数学思想的重要性，掌握数学思想才是真正“授人以渔”，才能让学生学会学习.如果评价仅仅考查基础知识和基本技能，则仍然停留在“双基”的基础上，无法体现课标理念，因此，让评价体现数学思想就显得尤为关键.如果设计评价练习时关注数学思想方法的渗透，就能让评价具有指导价值，不仅培养和指导学生感受和经历数学思想，还能指导学生运用数学思想去解决实际问题.

例如，对于百分率方面的问题，我们可以设计运用渗透数形结合、模型思想的评价练习：已知某温度下100 g的水最多能溶解100 g的糖，那么，在该温度下不断往水里倒糖，时间与含糖率的关系图像是（  ）.

本题考查学生将数与形结合、函数模型思想方法的运用，对于学生数学思想的发展有指导意义.学生要理解最多能溶解100 g的题意，即达到饱和后加再多的糖也不会提高浓度，即含糖率不会再改变.由此信息判断A是不符合题意的.而D选项的图像是一条水平线，说明一开始就保持含糖率不变，不符合往水里不断加糖，含糖率提高的实际情况.结合图像排除A，D后，分析B，C.100 g水溶解100 g糖，那么含糖率为100÷（100+100）×100%=50%，根据图像选择C.因此，数形结合的思想方法的运用能有效评价学生对实际情况含糖率的理解和掌握，渗透函数模型思想，为第三学段的函数学习奠定基础.因此，这样体现数学思想的评价练习，能指导学生进行理性分析、合情推理、图形象数，提高其数解释形的思维能力，促进其全面发展.

又如，在五年级学习长方体体积时，为了渗透极限思想、数形结合思想，培养学生的数感和空间观念，笔者设计如下评价练习：一个三层的长方体储物柜，占地面积1 m2，如图（隔层厚度不计）.

（1）如果每层高度在20～30 cm之间，那么它的体积可能是（  ）m3.

A.0.25  B.0.55  C.0.78  D.1

（2）如果每层高25 cm，那么请在下面线段中标出体积的位置，并说明理由.

这样的设计，锻炼学生的极限思想，指导学生用数学思想解决问题.先判断最矮高度20 cm和最高高度30 cm所测算出的总高度的范围是60～90 cm，进而判断长方体的体积区间.由长方体的体积，判断在数轴上的位置，既能数形结合训练数学思想，又能发展学生的数感和空间观念，对于学生能力培养和全面发展也有着重要的指导性意义和价值.

再如，五年级学习“一个数是另一个数的几分之几”的问题后，我们可以结合三角形三边关系的内容设计这样一道评价练习：一个三角形的三条边分别是a，b，c，如果b的长度是a的23，那么c的长度不可能是a的（  ）.

A.123B.113C.33或1 D.23

学生首先可以画一个三角形的草图，分别标上a，b，c三条边，再根据b的长度是a的23和一个数是另一个数几分之几的知识，推理出b的长度为2份，a的长度为3份，然后运用三角形三边的关系“两边之和大于第三边，两边之差小于第三边”的模型，推理判断c的长度范围是在2～4份之间，再结合一个数是另一个数的几分之几，就能得知c是a的23，33，43.本题以三角形三边的关系知识为载体，意在评价一个量是另一个量几分之几、假分数与带分数转化的知识，以及运用数学思想解决问题的能力.

三、体现思维素养——凸显评价的启发性

培根说：数学是思维的体操.思维能力和品格是数学学习过程中体现出来的最为重要的核心素养，也是数学学习的最终目标.良好的思维素养应该体现在课标中的“十大核心词”上，即让学生形成良好的数感、符号意识、运算能力、空间观念、几何直观、数据分析观念、逻辑推理、模型思想、应用意识、创新意识.而这些思维素养需要以评价为载体.我们需要优化练习的反馈过程，借此放大练习的价值.[2]我们可以通过适当的评价练习给予学生启发，进而对学生的思维进行培养和提升.多元评价练习可以启发学生開放性思维;应用评价练习可以启发学生应用性思维;结构评价练习可以启发学生结构化思维.

例如，为了启发引导学生的思维素养，我们可以设计这样的小数乘法评价练习：已知条件①一套丛书共4本;②这套丛书原价23.2元;③这套丛书现价17.4元;④A笔记本每本2.5元;⑤B笔记本每本3元.原来买丛书的钱，现在除了买丛书，还能买几本怎样的笔记本？（先填图，再解答，多种答案加分）解题时，首先需要学生理解丛书的原价和现价差，理清数量关系，培养数感.在线段图中表达数量关系，可以培养学生几何直观.在解决买几本笔记本的问题上，允许多元化解决问题，启发学生开放性思维和应用性思维，进而培养学生的创新意识和应用意识，同时也培养学生解决问题的能力.

又如，在设计三位数乘两位数的评价练习时，我们可以设计如下考查学生的数感和应用意识的练习，以启发学生的实践意识和思维素养：A电话每台128元，B电话每台108元，C电话每台198元，D电话每台210元.若只买一种电话50台，共花了□□□□0元，可能买的是（  ）.在解决这个问题时，首先启发学生考虑总价的数位问题，三位数乘两位数，积在四位数和五位数之间.而总价是五位数，学生需要有数感，知道最小的五位数是10000，根据数量关系，明白电话单价最少是200元，进而解决问题.这样的评价启发培养了学生的应用、数感，乃至知识结构化的思维素养.

再如，将五年级下册分数意义及性质单元的星号题改编如下：比14小，比15大的最简分数中，分母不可能是（  ）.

A.9B.13C.20D.40

学生受通分的定向思维影响，肯定关注到分母20和40两个选项，将原来两个分数通分后分别为520，420和1040，840，显然分母是20时，中间无法插入一个最简分数.但是许多学生会纠结选项A，B为什么可以.那是因为学生已经定向思维转化成同分母分数比较分数的大小，而淡忘了同分子分数比大小的方法.其实，运用分数的基本性质不难将原来两个分数转化成28，210和312，315，这样选项A和B分母分别为9，13就能理解了.本题重点评价学生是否掌握分数基本性质和灵活运用同分母分数和同分子分数比大小解决问题的能力，更为关键的是培养学生理性、多元化、非定式的思考方式，具有评价的启发性.

关注思考过程，能促进评价的针对性;关注数学思想，能增强评价的指导性;关注思维素养，能凸显评价的启发性，“三思”一体，最终形成有效的评价体系和模式，不仅让学生经历和感受知识产生和发展的过程，而且还能深度发展学生的能力和品格，培养适合终身发展的核心素养.

【参考文献】

[1]袁刚.小学数学练习课的评价激励实施策略[J].教育现代化 ，2018，5（34）：384-385.

[2]朱宇.优化课堂评价，“放大”小学数学练习的价值[J].教学与管理，2014（11）：35-37.