单指标非参数期权定价
——改进的非参数定价方法
李 庆,张 虎
(中南财经政法大学统计与数学学院,湖北 武汉 430073)
1 引言
期权是金融市场最活跃的交易产品之一,近年来中国期权市场迎来蓬勃发展。2015年2月9日,首个股票期权产品——上证50ETF期权上市交易;2017年上市了豆粕期权和白糖期权两个期权品种;2018年上市了铜期权;2019年更是上市了玉米期权、棉花期权、天然橡胶期权、铁矿石期权、PTA期权、甲醇期权、黄金期权、沪深300股指期权和沪深300ETF期权(2只)等10个期权品种,这些期权产品将逐渐增强中国金融市场系统性风险管理功能和金融衍生品市场服务实体经济的能力。
期权价格的精确估计是进行风险管理和服务实体经济的基础,现有期权定价模型都是建立在欧美国家期权市场比较发达的基础上,发达国家期权市场交易机制完善、市场流动性好,期权价格估计精确度较高。但是,中国的期权市场上市时间较短、交易机制不够完善和市场交易数据少,套用现有期权定价模型无法有效的估计中国期权价格数据,寻求符合中国期权市场实际的定价方法需要进一步的研究。
自从Black 和Scholes[1]在期权的标的资产价格服从扩散模型基础上建立经典的Black-Scholes期权定价模型以来,学者们不断对扩散模型进行改进并得到相应的期权定价模型,如Merton[2], Bates[3],Madan等[4]建立的跳扩散期权价格模型,Heston[5]建立的随机波动率模型,Heston和Nandi[6]得到标的资产价格服从GARCH模型的封闭式期权定价公式,吴鑫育等[7-9]对随机波动率模型进行改进建立非仿射随机波动率期权定价模型,我们称这些模型为基于参数扩散过程的期权定价模型。
尽管各种改进的参数扩散模型越来越复杂,实际上期权价格的估计精度也没有显著的提高。从而,学者们把扩散方程设定为非参数形式,建立了基于非参数扩散过程的期权定价模型,Ait-Sahalia[10]首次假定利率方程为非参数扩散模型,得到非参数形式的利率衍生产品定价公式。Fan Jianqing[11]对扩散模型所有非参数和半参数形式和相应的期权定价公式相比较。Kenmoe和Sanfelici[12]使用非参数核估计方法估计扩散系数和伊藤过程,研究基于高频数据的衍生品定价,得到基于高频数据时波动率的估计效果比使用日度数据的好。Kung[13]使用非参数核估计方法估计波动率,然后使用蒙特卡洛模拟方法计算期权价格。韩立岩等[14]则使用非参数扩散模型实证分析恒生指数期权,得到基于非参数过程的期权定价效果优于Black-Scholes期权定价模型。
然而,无论是复杂形式的参数扩散模型还是非参数扩散模型,都仅仅是对扩散过程波动率的估计方法进行了改进,没有体现期权数据的特点,因为都是使用标的资产价格历史数据,得到的波动率只能反映“过去”的波动情况(历史波动率),期权价格反映的 “未来”波动的预期(隐含波动率)没有体现,没有使用期权市场交易数据信息(Dumas等[15])。此外,现有扩散期权定价模型都是建立在期权价格和各个影响因素满足特定函数形式基础上的,实际上期权价格关于各个因素的具体函数关系是未知的。鉴于现有期权定价方法的模型假定误差缺陷,非参数回归期权定价方法从期权交易数据出发,无需假定期权价格与各因素满足具体的函数形式,完全由数据驱动更加符合实际。
Ait-Sahalia和Lo[16,17]最早提出非参数回归期权定价理论,建立期权价格关于期权价格因素的多元非参数回归模型(降维前包含标的资产价格、行权价格、行权期限等5个因素,降维后为价值状态和行权期限2个因素),并使用核估计方法进行估计。沿着Ait-Sahalia和Lo[16,17]思路,Fan和Mancini[18]首先使用参数期权定价模型估计期权价格,然后使用非参数方法对定价误差进行修正,建立了模型指导的非参数修正期权定价模型, 进一步提高了定价精确度,收敛速度也快于Ait-Sahalia和Lo[16]模型。针对Ait-Sahalia和Lo[16,17],Fan和Mancini[18]仅使用历史波动率或隐含波动率单一波动率,Song Zhaogang和Xiu Dacheng[19]构建了包含多个波动率因素的非参数回归期权定价模型,期权价格估计效果更好。Marinelli和d’Addona[20]在Ait-Sahalia和Lo[16]的半参数Black-Scholes期权模型框架下,通过线性插值法估计隐含波动率表面估计的期权价格,无论是计算精确度还是计算速度都优于非参数核估计方法估计隐含波动率估计的期权价格。
非参数回归期权定价方法解决了模型设定误差问题,然而非参数估计方法需要大量的样本数据,而在给定的某一交易日交割的期权价格数据又较少(20~50个),所以非参数定价方法往往需要按时间滚动期权价格数据集的方法(Aggregate data over time)来增加样本数量,如Ait-Sahalia和Lo[16]采用1年时间的期权数据集(14431对期权价格数据),Fan和Mancini[18]采用3年时间的期权数据集(101036对期权价格数据),并且使用截面和时间的二维滚动模型解决了样本量小的问题。但是,Ludwig[21]认为按时间滚动的数据集方法虽然解决了样本数量问题,但是采取二维模型使得数据在行权期限上具有跳跃性,导致样本数据非平稳和日历套利效应。
现有非参数回归期权定价模型把多个不同期限结构的期权合约组合(同一行权期限下不同行权价格合约)集合在一起进行非参数回归时,忽略了期限结构对期权定价结果的影响,容易产生非平稳性和日历效应。此外,使用实际期权交易价格数据进行实证分析估计期权价格时,把隐含波动率高、行权期限较长和较短等流动性差的期权合约数据删除,这种有选择性的样本数据,使得样本内的估计效果好,但是样本外的预测效果较差(Ait-Sahalia和Lo[16],Fan和Mancini[18])。
针对现有非参数回归期权定价模型忽视行权期限长、交易量少、隐含波动率高等流动性差的期权合约问题,Vogt[22]建立一种新的非参数估计方法,构建围绕风险中性价值方程的期权价格Sieve估计量。不同于Ait-Sahalia和Lo[16]、Fan和Mancini[18]、Song Zhaogang和Xiu Dacheng[19]等现有非参数回归期权定价方法通过期权价格近似估计状态价格概率密度函数或分布函数计算期权价格,Vogt[22]通过变量变换得到期权价格关于随机变量的积分函数使得计算更加方便。
本文的研究思路为,使用Vogt[22]的变量变换方法把期权价格关于行权价格的函数转化为期权价格关于综合指标的函数,其中综合指标是期权价格因素的合成指标(综合指标是标的资产价格、行权价格、行权期限、无风险利率、股息率和隐含波动率等期权所有因素的合成指标);并且进一步借鉴Fan和Mancini[18]把期权价格公式转化为非参数回归函数的处理,把Ait-Sahalia和Lo[16]的非参数期权定价方法进行改进为期权价格关于综合指标的一元非参数回归函数,最终实现不同行权期限结构的期权合约组合(每个行权期限包含多个行权价格期权合约),有效的解决了期权价格合约数量少的问题;还实现了不同期权结构期权数据的平滑处理。
计算的步骤为,假定资产价格服从Black-Scholes随机微分方程,通过变量变换把看跌期权价格支付函数由原来关于状态价格的积分函数,转化为关于误差项随机变量的积分函数,变换后的积分函数中积分上限是期权价格因素综合指标的积分函数,并把积分函数离散化为一元非参数回归方程(期权价格关于综合指标的回归方程),最后使用局部多项式方法估计出期权价格。本文把这个综合指标称为单指标,期权价格关于单指标的非参数模型我们称为单指标非参数期权定价模型。
相比现有非参数期权定价方法,本文建立的单指标非参数期权定价模型有三个优势,一是减少了计算量,不需要先使用非参数近似估计状态价格概率密度函数再求解期权价格,直接得到期权价格关于价格因素单指标的非参数回归方程;二是实现了降维,把期权价格的多元非参数回归模型转化一元非参数回归模型;三是解决非参数回归时期权合约数据量少的问题,以及不同期限期权合约产生的非平稳性和日历效应问题。
2 非参数期权定价模型

(1)
相比各种假定的参数期权定价模型(Black 和Scholes[1],Heston[5]等),Ait-Sahalia 和Lo[16]认为期权价格与期权价格各个因素的函数关系是未知的,他们使用非参数方法估计期权价格,假定期权价格是状态变量Z=(S,κ,τ,r,δ)的非参数回归函数:
Pi=P(Zi)+εii=1,2,…,n
(2)
其中P(.)是未知的平滑函数,Z=(S,κ,τ,r,δ),S,κ,τ,r,δ分别为前面定义的期权价格的标的资产价格,行权价格,行权期限,无风险利率和股息率5个影响因素,随机误差项εi是白噪声的。
未知的非参数函数P(.)使用多元核估计(也可以使用局部多项式估计):
(3)
以上期权公式有5个变量,其中的核函数为多元核,而且多元核可以表示为5个一维核的乘积形式:
(4)
当自变量个数较多时,式(3)中有5个变量,非参数估计量的精确度会降低,所以需要降低自变量的维数,Ait-Sahalia 和Lo[16]采用的降维方法之一是根据金融原理进行的,根据远期价格Ft,τ=Ste(rt,τ-δt,τ)τ,定义价值状态m=κ/Ft,τ(mt,i=κi/Ft,τ),而且无风险利率在一定时间内保持不变,则期权价格降低为价值状态mt,i和行权期限τ的二元函数:
另外一种方法是Black-Scholes模型中的波动率是隐含波动率,称为半参数Black-Scholes模型,Ait-Sahalia 和Lo[16]是看涨期权价格,我们对应给出看跌期权价格:
PSemi-BS=e-rt,ττκN(d(Z))-S0N(d(Z)-σ(Z))
(5)

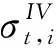
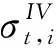
(6)
然而,二次函数不能有效的拟合隐含波动率与价值状态的关系,Fan和Mancini[18]把关于价值状态的隐含波动率函数扩展到非参数形式:
(7)
其中g(.)是未知的平滑函数,可以通过核估计、局部线性估计等非参数方法估计得到。
3 单指标非参数期权定价模型
3.1 单指标非参数定价模型的建立
假定Bt是时变的随机变量,期权标的资产价格是关于随机变量的方程:
log(St/S0)=μ(Z)+σ(Z)Bt
(8)
其中μ(Z)是漂移系数,σ(Z)是扩散系数,并且Z=(S,κ,τ,r,δ);随机变量Bt~f0(.|τ),而且f0(.|τ)可以是特定概率密度函数(如正态分布),也可以是非参数形式的概率密度函数。
从方程(8),我们可以得到状态价格St=S0exp[μ(Z)+σ(Z)Bt],以及把随机变量Bt表达为状态价格St的函数:
Bt=(log(S/S0)-μ(Z))/σ(Z)
(9)
根据随机变量代换式(9),得到期权价格关于随机变量Bt的积分函数:

(10)

从公式(10)可知,变量变换后期权价格变为关于随机变量Bt的积分函数(积分上限是单指标d(Z)),即把期权价格所有因素全部合并成单指标,实现了模型降维。


为了便于积分,做变量变换:
x=Bt-σ(Z)
=e-rτκN(d(Z))-S0e-δτN(d(Z)-σ(Z))
=PBS(f0,Z)
(11)

建立的单指标模型将通过变量变换把期权价格的五个影响因素Z=(S,κ,τ,r,δ)变换为随机变量Bt的积分函数,可以得到看跌期权价格关于单指标变量d(Z)的回归方程:


(12)
(13)
所以(12)式又可以表达为:

(14)
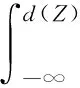
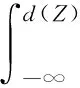
(15)
根据(15),我们可以得到如下一元非参数回归方程:
Yi=G(Xi)+εii=1,2,…,n
(16)
其中G(.)是待估计的未知函数,随机误差项εi是白噪声,即εi~i.i.d(0,σ2),并且回归方程中变量为:
根据非参数估计方程(16)得到的期权价格估计量为:
(17)
相对于Ait-Sahalia 和Lo[16]的期权价格关于标的资产价格、行权价格等因素的多元非参数模型,以及Fan和Mancini[18]的期权价格变化函数(单位行权价格内期权价格变化)关于价值状态(行权价格/远期价格)的一元非参数模型;Vogt[22]使用变换的密度代入(14)得到期权价格的封闭形式,单指标模型则是期权价格变量(期权价格的变形)关于单指标(包含标的资产、行权价格等所有因素)的一元非参数回归模型。
3.2 期权价格的局部线性估计

G(Xi)≈G(x)+G′(x)(Xi-x)
(18)
令系数β0=G(x),β1=G′(x),把泰勒展开式表示为G(Xi)≈β0+β1(Xi-x)。
使用局部加权最小二乘估计方法估计未知函数G(Xi), 即求解下式的最小化问题:
(19)

为了表达更加方便,记系数矩阵β=(β0,β1)T,最小化问题(19)表达为矩阵形式,
(20)
其中:
核函数K(z)=0.75(1-z2)I(|z|<1)。
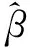
(21)
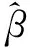
即为β的局部线性估计量,其中第一个元素为G(x)的局部线性估计量,第二个元素为一阶导数G′(x)对应分量的局部线性估计量。
3.3 局部线性估计的窗宽选择
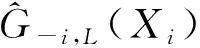

(22)
即
(23)
从而,LSCV最优窗宽为:
(24)
此外,Li和Racine[24]经过数值模拟得到,当
h=3.45σxn-1/5
(25)
时估计精确度最高,其中σx是回归变量的标准差,n是估计样本的数量。所以,这里我们选择的窗宽是h=3.45σxn-1/5。
4 实证分析
4.1 数据选取
现有研究中Ait-Sahalia和Lo[16],Fan和Mancini[18]等选取美国芝加哥期货交易所(CBOE)的S&P500指数(SPX) 欧式看涨期权数据进行实证分析,研究不同期权定价模型定价精度。上证50ETF期权是中国第一个期权产品,本文选取上海证券交易所交易的上证50ETF期权实证分析,由于看跌期权价格变化比看涨期权更难估计,所以我们对看跌期权价格进行估计。中国上海证券交易所上证50ETF期权于2015年2月9日上市,上证50ETF期权的标的物为上证50ETF,上证50ETF数据和期权合约数据从大智慧软件获得,行权价格间隔为3元或以下为0.05元,3元至5元(含)为0.1元。
选取样本为2015年3月、4月、5月、6月、7月、8月和9月共七个月的认沽期权合约,为了保持期权合约的流动性(Ait-Sahalia和Lo[16]),我们删除隐含波动率无法得到和高于70%的期权合约,期权价格低于0.05的期权合约(行权价格间隔为0.05),期权到期日(日历时间)少于1天的期权合约,一共得到3531个观测样本。无风险利率从中国人民银行货币司选取(一年存款利率),其中2015年一年期定期存款利率为r=2.25%。
4.2 期权定价求解与定价效果评估
所有的期权合约按照价值状态m的大小分为虚值期权、平值期权和实值期权,我们参照Fan和Mancini[18]的划分标准,不过本文是看跌期权(认沽期权),所以我们的划分为:如果m<0.94,期权为虚值期权(in-the-money,ITM);如果0.94≤m<1.04,期权为平值期权(at-the-money,ATM);如果1.04≤m,期权为实值期权(out-of-the-money,OTM)。
定价后使用定价误差相关指标评估定价效果,如Minimum, maximum, mean, Std. Dev是定价误差 (u=Pmodel-Pmarket) 的最小值、最大值、均值和标准差;RMSE 是均方根误差 (Root Mean Square Error),均方根误差表达式为:
(26)
MAE是平均绝对误差 (Mean Absolute Error),平均绝对误差表达式为:
(27)
4.3 样本内估计
选取样本内数据使用模型进行实证分析,表1给出了样本内数据四个期权定价模型的定价效果,从相对定价误差MAE数值可以得到,单指标非参数模型具有最好的定价效果,而且定价效果明显优于Black-Scholes模型,非参数回归定价模型和半参数Black-Scholes模型。模型单指标非参数模型有最小的MAE值(0.08450),明显优于其他模型;而Black-Scholes模型的MAE值为0.459366,非参数和半参数Black-Scholes模型的MAE值分别为0.242303,0.233587。
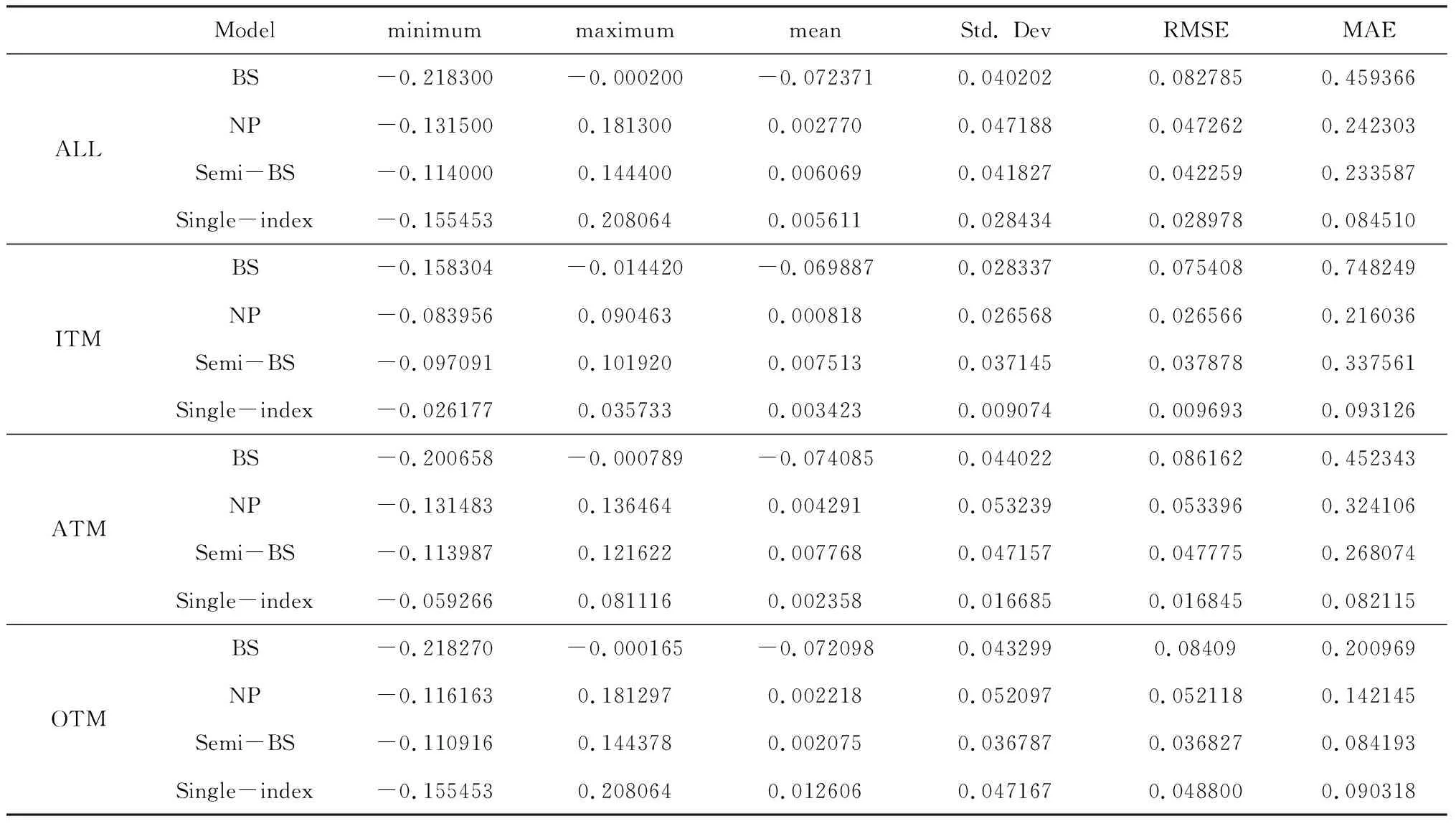
表1 样本内期权价格估计结果
图1是95%置信水平下隐含波动率的非参数局部线性估计效果图,符合常见的波动率微笑图,但是比二次函数抛物线更加精确的描述波动率微笑。图2是95%置信水平下期权价格方程的非参数估计效果图。从图1和图2中可以看出,我们选取的带宽对于非参数估计量的估计具有较好的效果。

图1 隐含波动率方程(7)的非参数估计

图2 期权价格方程(16)的非参数估计
图3~图6给出了四个模型定价结果残差直方图,从图3~图6的四个图可以看出Single-index模型定价残差图更窄,而且残差值更多集中于0附近,近似服从正态分布,进一步说明了本文建立的单指标非参数模型定价效果更好。
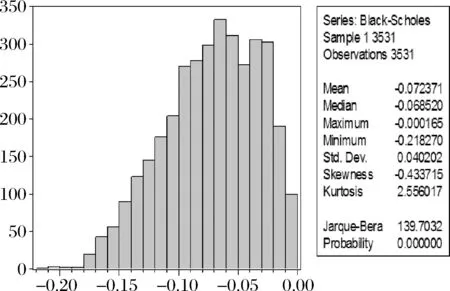
图3 Black-Scholes模型定价误差直方图

图4 NP模型定价误差直方图
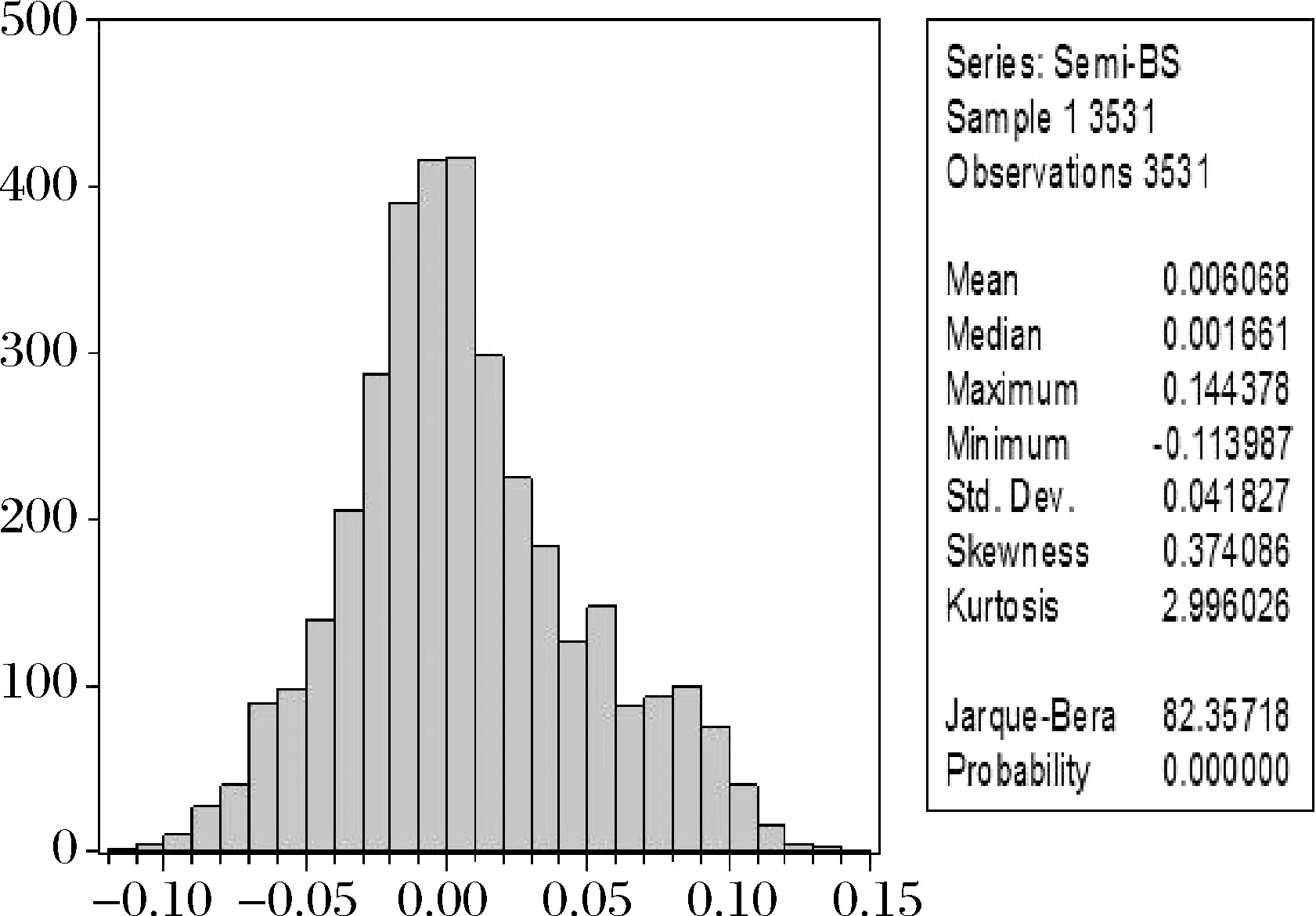
图5 Semi-BS定价误差直方图
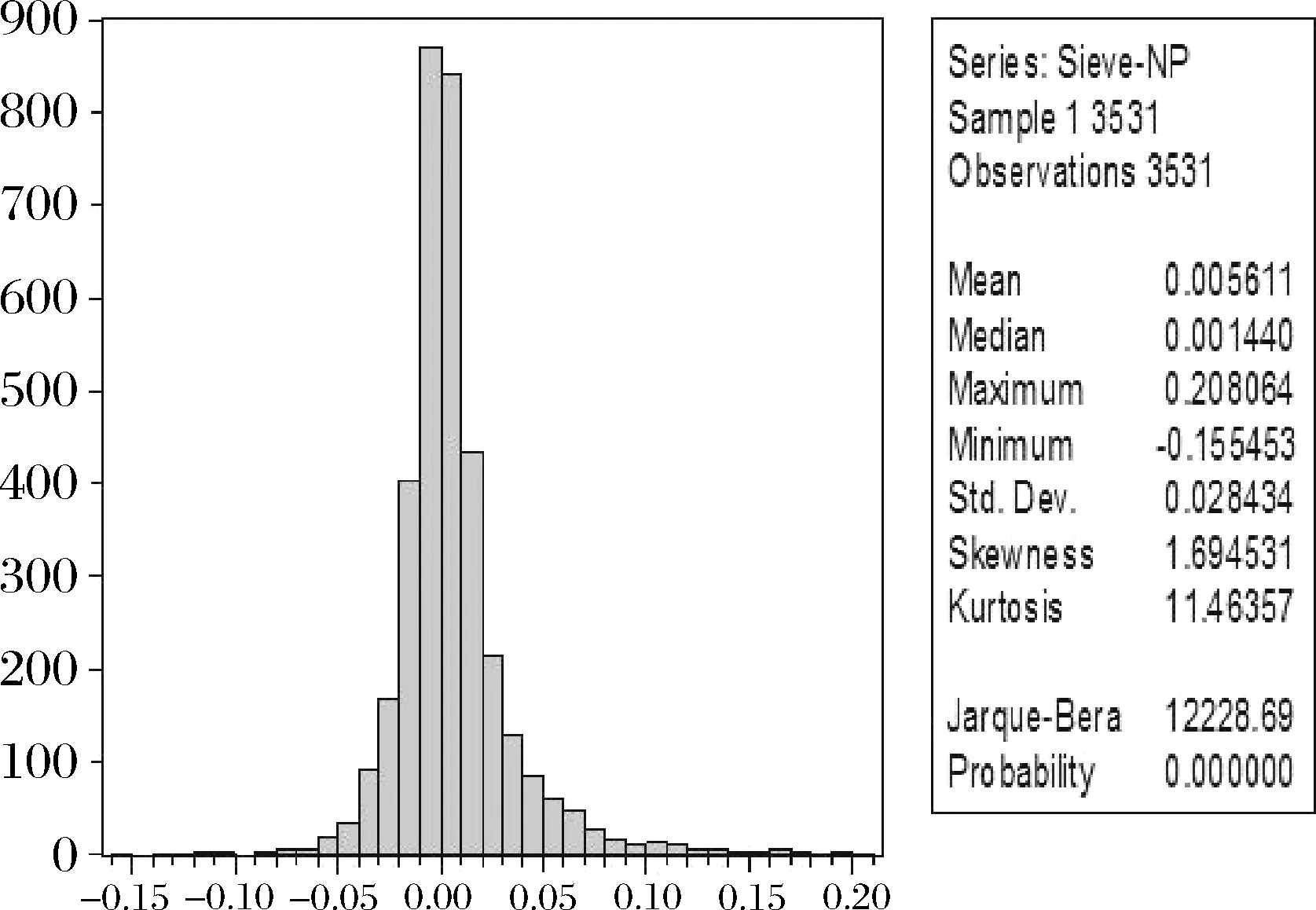
图6 Single-index模型定价误差直方图
4.4 样本外预测
为了进一步的检验模型的估计效果,我们选取样本外的期权合约数据进行。预测样本为2015年8月24日-2015年9月9日期间,2015年9月、10月、12月和2016年3月共四个月份1007个看跌期权合约样本,删除不合格样本最后剩下907个样本数据。
因为股息率无法观测到,为了预测远期价格,所以我们从期权看跌-看涨平价公式Ft,τ=(Ct-Pt)ert,ττ+κ=Ste(rt,τ-δt,τ)τ,得到隐含股息率δt,τ:
(28)
通过计算,求解股息率平均值为1.715%。
Fan和Mancini[18]使用局部线性估计方法拟合隐含波动率,这里也使用局部线性估计隐含波动率:
(29)

(30)

根据以上步骤,计算得到样本外期权价格预测值在表2,根据表2可以得到,对于整个样本,单指标非参数模型的MAE值相比其他模型更小,单指标模型的MAE值为0.390387,非参数回归和半参数Black-Scholes模型的MAE值分别为0.400953,0.449783。但是和样本内的优势相比,样本外预测值的效果优势较低,单指标非参数模型只是略微高于非参数回归模型和半参数Black-Scholes模型。

表2 样本外期权价格预测结果

续表2 样本外期权价格预测结果
5 结语
本文建立的单指标非参数期权定价模型给出了经典Black-Scholes期权定价公式的一种新的证明。这种模型相对现有非参数期权定价模型优点体现在:相比经典的Black-Scholes期权定价模型和半参数Black-Scholes期权定价模型,单指标非参数期权定价模型对随机误差项服从的正态分布的假定条件放宽,不假定随机误差服从具体的参数分布,而是使用非参数形式,更加符合实际情况;相比经典的多元非参数回归期权定价模型关于价值状态和行权期限的二维变量,本模型把期权价格五个影响因素Z=Z(S,κ,τ,r,δ)和波动率σ转化为一元变量d(Z),非参数期权定价模型转化为一维非参数回归模型,实现了估计模型的进一步降维,使得期权价格估计更加方便,减少了计算量提高了计算精确度;单指标非参数模型把期权价格五个因素归结在一起,把不同行权期限的期权合约(每个行权期限包含多个行权价格期权合约)形成组合,得到期权价格表面(行权期限和行权价格的组合),有效的拓展了可以计算的样本数量,解决非参数回归时期权合约数据量少的问题,以及不同期限期权合约产生的非平稳性和日历效应问题,最终提高了非参数估计精确度。但是,模型还可以进一步的改进,就是对于较小数值的期权价格估计偏差比较大,尤其是模型预测部分,后续的研究中我们将从两个方向对本模型进行改进,先使用参数或半参数模型定价,然后再使用本文模型进行非参数修正,进一步降低估计误差。
——基于SZH的案例研究

