基于混频数据模型的宏观经济对股票市场波动的长期动态影响研究

刘凤根，吴军传，杨希特，欧阳资生

(湖南工商大学财政金融学院，湖南 长沙 410205)

1 引言

美国30年代大危机至今一系列金融危机爆发的经验事实表明，任何外生冲击引发金融危机之后，股票价格的恐慌式下跌必然加剧金融危机。特别是2008年美国次贷危机以来，股票市场异常波动作为系统性金融风险的重要引致因素(Giglio等)[1]已经成为金融监管当局管理系统性金融风险的重要内容。近几年来，受宏观经济下行压力加大、“去杠杆”、“调结构”、中美贸易摩擦等诸多不确定性因素的影响，中国股票市场经历的多次暴涨暴跌对“牢牢守住不发生系统性金融风险”工作形成了严峻挑战。因此，准确判研宏观经济与股票市场波动的关系，减少“下行的宏观基本面”对股票市场波动的冲击，对防范化解“股票市场异常波动型”系统性金融风险的发生具有重要作用。

宏观经济与股票市场波动之间的关系是宏观金融理论研究的一个经典命题。Campbell和Cochrane[2]的习惯形成模型、Reitz[3]和Barro[4]的罕见灾害模型等经典主流理论得出基本一致的结论是，宏观经济变化通过对边际效用、资本成本和贴现率等因素的影响，最终引致股票价格变化。股票价格具有顺经济周期性，而股权溢价和股票价格波动具有逆经济周期性特征，即经济衰退时股票价格波动性更大，经济繁荣时股票价格波动性变小。来自美国等发达市场(Fama和Schwert[5]；Ferson和Harvey[6]；等等)和新兴市场(Levine 和Zervos[7]；赵振全和张宇[8]；等等)大量实证证据支持了这一结论。

传统计量方法在处理宏观经济与股票价格之间的关系时存在两个不可规避的难点：①传统计量模型关于解释变量和被解释变量数据频率的一致性要求与事实上可获得的宏观经济变量时间序列和股票价格时间序列原始数据的不同频产生了矛盾。按照统计惯例，GDP通常以季度频率进行统计并公布，CPI、PPI等其他宏观经济变量数据以月度频率进行统计并公布。而以日频率以及日内分钟为采集频率的中高频股票价格时间序列数据由于含有高度持续性的交易信息，更加准确地揭示了股票价格行为特征，为股票市场波动性研究文献所推崇。为了使这两类数据同频，学术界通常采用插值法将低频数据转换为高频数据(Chow和Lin[9]；赵进文和薛艳，2009[10])，或采用加总、替代方法将高频数据转换为低频数据(Silvestrini和Veredas)[11]。毫无疑问，这些数据变频方法都会损失原始数据本身所蕴含的有效信息并可能引起模型误设和统计偏误(Ghysels等)[12]。②传统的VAR、SVAR、GARCH、Copula等被广泛运用于宏观经济变量对股票市场波动影响的计量方法，事实上无法准确识别宏观经济变量对股票市场波动的内在影响机制。虽然自Engle和Lee[13]提出CGARCH模型之后一系列成分GARCH模型将股票收益率序列的条件方差(波动性)分解为与波动性新息短暂效应相关的短期波动及与持久效应相关的长期波动两种成分，但这类成分模型仅仅局限于股票收益率序列的波动性成分分解层面，对于不同的波动性成分特别是长期成分的驱动因素却无法识别，更无法解释其经济含义。

混频抽样(Ghysels等，2007)[12]通过引入权重多项式实现了低频数据与高频数据的有机结合，规避了传统计量模型关于解释变量与被解释变量数据频率的一致性要求。大量的混频抽样模型运用于宏观经济变量预测(刘汉和刘金全[14]；李正辉和郑玉航[15]；鲁万波和杨冬[16])并证实比传统计量模型具有更好的计量功效。Engle等[17]首次建立混频自回归条件异方差模型(GARCH-MIDAS)将股票收益率序列的高频波动分解为短期成分和长期成分并运用混频抽样实证分析了通货膨胀、工业产值增长率对股票收益率序列波动长期成分的影响，为探究宏观经济与股票市场波动的动态关系提供了一个有效的混频数据模型分析框架。郑挺国和尚玉皇[18]关于中国股票市场日波动率的样本内拟合和样本外预测、Asgharian等[19]关于美国宏观经济不确定性对股票市场与债券市场长期波动的影响、夏婷和闻岳春[20]关于中国宏观经济不确定性对股票市场长期波动的影响等研究均表明GARCH-MIDAS模型的适用性并能够提高计量功效。

鉴于当前中国经济结构性减速的“经济新常态”特征事实，本文基于Engle等[17]的分析框架，首先将上证综指日收益率的已实现波动率分解为短期波动成分和长期波动成分；其次选取生产者价格指数(PPI)、居民消费价格指数(CPI)、宏观经济景气指数(CONS)、同业拆借利率(RATE)四个主要宏观经济变量，运用混频抽样方法实证分析了宏观经济对股票市场波动长期成分的动态影响。与以往文献相比，这一研究的边际贡献是：①运用混频抽样方法实证分析了中国宏观经济变量对股票市场波动的影响，避免了因数据同频处理过程中所引起的样本信息损失、人为的信息虚增并可能引发模型误设和统计偏误，增强了计量结果的准确性和可信度；②考虑到不同宏观经济变量对股票市场波动具有不同的作用机制，而且同一宏观经济变量在水平值和波动率两个维度对股票市场长期波动也具有不同的影响效果，本文不仅单独考察了PPI、CPI、CONS和RATE四个主要宏观经济变量对股票市场波动的长期动态影响，而且运用主成分分析方法提取了第一主成分(PC1)以及构建了一个能全面反映宏观经济总体运行状况的综合指数(MACRO)进一步进行了实证分析，既探究了宏观经济总体状况对股票市场波动的影响，又克服了GARCH-MIDAS模型的滤波方程不能同时嵌入多个宏观经济变量的缺陷；③基于多因子GARCH-MIDAS模型中宏观经济变量对股票市场长期波动影响系数的衰减变化，系统地探究了各个宏观经济变量对股票市场波动的动态影响机制。

2 模型设定

2.1 股票市场波动率单因子GARCH-MIDAS模型

根据Campbell和Shiller[21]及Campbell[22]的经典分析框架，任何股票市场的非预期收益可以设定为：

(1)

其中，ri,t表示第t月第i天的股票市场收益率，di,t为第t月第i天的股票市场股利，ρ为贴现因子，Ei-1,t(·)表示给定已知的直到i-1时刻为止的信息集Ii-1,t情形下的条件期望值。

Engle和Rangle[23]认为，非预期收益可以被描述为对未来现金流或预期收益的新息，且股票市场预期收益受到新息冲击之后具有时变方差，即：

(2)

因此，股票收益率序列的波动性被分解为高频的短期成分gi,t和低频的长期成分τt。其中，gi,t表示第t月第i天的高频波动率，τt表示第t月的低频波动率，并假定随机扰动项εi,t服从条件标准正态分布，即εit|Ii-1,t～N(0,1)。

这样，股票收益率序列的总条件方差可以表示为：

(3)

假设Ei-1,t(ri,t)=μ，方程(2)可以写成：

(4)

假设股票收益率序列的短期波动成分gi,t遵从GARCH(1,1)过程，即：

(5)

长期波动成分τt为一个已实现波动率RVt的MIDAS滤波方程，即：

(6)

其中，参数θ度量的是已实现波动率RV对于股票收益率序列波动率长期成分τt的边际贡献，K为平滑滤波的最大滞后期数并依模型而定。已实现波动率定义为：

(7)

(8)

其中，N表示第t月有N天，参照Engle等[17]的做法，N=22。(6)式和(7)式分别定义的是固定窗口的已实现波动率和滚动窗口的已实现波动率。

(6)式中的φj(ω1,ω2)是通过β函数构造的权重方程并定义为：

(9)

(4)-(9)式即构成了基于已实现波动率的单因子GARCH-MIDAS模型。

2.2 纳入宏观经济变量的股票市场波动率多因子GARCH-MIDAS模型

很多主流金融理论(Schwer[24]、Kim和Nelson[25]等)研究表明，从波动性成分来看，股票市场波动中的短期成分呈现出显著的均值回复特征，对市场中突发信息非常敏感；而长期成分主要受到宏观基本面新息的驱动。根据Engle和Rangle[23]，以Xt表示宏观经济状态变量，则上述(4)式就可以修正为：

(10)

由此，上述描述股票收益率序列波动性长期成分模型修正如下：

(11)

这样，宏观经济变量的低频数据就通过MIDAS滤波的方式与股票收益率序列的中高频数据实现了有机结合。

为了充分考察宏观经济变量X对股票市场波动率的影响，本文分别从水平值XL和波动率XV两个维度测度宏观经济变量对股票收益率长期波动成分产生的影响。因此，一个同时考察已实现波动性和宏观经济变量对股票收益率序列长期波动成分τt的影响模型的具体形式设定为：

(12)

考虑到宏观经济变量的符号有正有负，对上式中的τt取对数就可以保证与总条件方差的符号始终为正相匹配。采用大多数文献的做法，具体实证实施过程中，采用τt的对数形式。

由此，单因子GARCH-MIDAS模型即被拓展为一个纳入宏观经济变量的股票市场波动率多因子GARCH-MIDAS模型，本文简称为RV+XL+XV模型。

出于模型的可识别和收敛问题，上述多因子GARCH-MIDAS模型只能考察一个宏观经济变量对股票市场长期波动的影响。为了规避多因子GARCH-MIDAS模型的这一缺陷，借鉴Asgharian等(2013)[26]的做法，本文运用主成分分析获得第一主成分PC1并构造一个能充分反映宏观经济总体状况的综合指数MACRO。假设存在q个宏观经济变量Xi(i=1,2，…，q)，则第i个主成分可以表示为：

PCi=v1iX1+v2iX2+…+vqiXq

(13)

其中，系数向量Vi=(v1i,v2i,…,vqi)为向量X=(X1,X2,…,Xq)的协方差矩阵或相关系数矩阵的第i个特征值λi所对应的特征向量，并且在各主成分中，第i个主成分PCi的方差为var(PCi)=λi，PC1的方差最大，PC2的方差次之，…，PCq的方差最小。如果主成分是通过协方差获得，则要求对Xi进行均值化处理；如果运用相关系数矩阵获得主成分，则需要对Xi进行标准化处理，如0-1标准化、正态标准化等。

一个能够有效替代q个原始宏观经济变量的综合变量的最优选择即为第一主成分PC1。但是，第一主成分作为综合指标的前提是其方差贡献率足够大，通常情况下这一条件较难得到满足，表明单纯使用PC1可能存在精确性不足的问题(林海明和杜子芳，2013)[27]。鉴于此，本文进一步构造一个宏观经济综合指数MACRO，即通过各个主成分的特征根占所有特征根之和的比例作为权重对所有主成分进行加权求和获得的MACRO指数定义如下：

(14)

这样，将(9)式中单个宏观经济变量X替代为PC1和MACRO，就可以分别建立纳入宏观经济主成分多因子GARCH-MIDAS模型和宏观经济综合指数GARCH-MIDAS模型综合考察宏观经济总体状况与股票市场波动的长期动态关系。

3 实证研究

3.1 变量选取和数据说明

本文选取上证综合指数收益率的增长率度量股票市场波动性。代表性选取生产者价格指数(PPI)、居民消费价格指数(CPI)、宏观经济景气指数中的一致指数(CONS)和同业拆借利率(RATE)四个宏观经济变量测度宏观经济基本面。实证分析中宏观经济变量的水平值和波动率分别取为各宏观经济指标的增长率及其波动率。参考Schwert[24]的研究，对宏观经济变量水平值取对数并进行一阶差分之后，进行关于12个月度虚拟变量的AR(p)自回归，将获得的残差平方作为宏观经济变量波动率的代理变量。考虑到银行同业拆借利率是中国最早实行市场化的利率，银行间同业拆借市场中7天同业拆借交易最为活跃，交易量也最大，本文采用银行间同业拆借7天加权平均利率作为同业拆借利率的代表。上证综合指数为日度数据，宏观经济变量为月度数据，数据区间为1996年1月～2018年12月。所有数据均来自Wind数据库。

3.2 GARCH-MIDAS模型的估计

在对单因子和多因子GARCH-MIDAS模型进行估计过程中，均依据准极大似然估计法(QML，Quasi Maximum Likelihood Estimation)，综合运用AIC、BIC信息准则最小和似然比函数值LLF最大原则进行选择。本文在估计过程中，对于权重函数的权重和MIDAS滤波方程的MIDAS滞后年的取值问题处理如下：遵循Engle等[17]的做法，第一个权重取值为ω1=1，而第二个权重ω2的值则通过模型估计自行选择，从而保证了滞后期数越长对应的权重越小。MIDAS滤波方程中滞后期数K或MIDAS滞后年由模型和数据自行决定，即利用信息准则最小和似然比函数值最大以及最后1期滞后权重为零(此时信息提取最完全)作为选择最佳滞后期的标准，同时结合股票市场波动的长期成分与股票市场波动的总条件方差的拟合程度进行辅助选择。实证研究发现：①当MIDAS滞后年取为1时，滞后K=12期的权重不为零，此时信息提取不完全，所以不讨论MIDAS滞后年为1的情形；②不论是固定窗口模型还是滚动窗口模型，随着MIDAS滞后年的增加，似然比函数逐渐减少，而信息准则不断增加。所以GARCH-MIDAS模型的最佳MIDAS滞后年为2或MIDAS滞后期K取值为24。最后，本文仍然综合运用信息准则最小与似然比函数值最大原则对固定窗口模型和滚动窗口模型进行选择。

(1)单因子GARCH-MIDAS模型估计

表1为参数Θ={μ,α,β,θ,ω,m}的估计结果。不论是固定窗口模型还是滚动窗口模型，度量GARCH效应的参数μ,α,β在统计意义上显著，说明中国股票市场短期波动呈现出显著的波动集聚效应，这与刘凤根和周驭舰(2018)[28]等采用传统的GARCH模型所获得研究结论一致，表明中国股票市场波动存在显著的短期尾部风险；度量已实现波动率对于股票市场波动率长期成分的边际贡献参数θ的估计值均显著为正，意味着已实现波动率增加了股票市场的长期波动。以上结论揭示了GARCH-MIDAS模型在中国证券市场中的适用性。

表1 股票市场波动率的单因子GARCH-MIDAS模型的估计结果

综合运用信息准则和似然比函数值选择的结果可以发现，滚动窗口GARCH-MIDAS模型明显优于固定窗口GARCH-MIDAS模型。从滚动窗口的估计结果来看，系数θ=0.0372，β权重函数中ω=10.0780，将赋予滞后j期的权重为φj(ω)，则已实现波动率RV对股票市场波动的长期成分τ的影响程度可以由100×θ·φj(ω)计算获得。由此可以得知，滞后1期的权重为φ1=0.3552，滞后2期权重为φ2=0.2373，权重的大小逐渐减小，滞后10期以后权重系数几乎为零，意味着已实现波动率当期增加1%，则下一期股票市场波动的长期成分将增加1.32%，滞后2期将增加0.88%，直至第10期后其影响才消失，显示出中国股票市场风险具有较强的持续效应。

(2)多因子GARCH-MIDAS模型估计

本文首先对所选取的四个宏观经济原始指标进行正态标准化处理，再运用协方差矩阵进行主成分分析。从表2列示的各个主成分与宏观经济变量间的相关系数来看，第一主成分PC1与PPI、CPI、CONS和RATE的相关系数分别为0.7369、0.6748、0.4923、0.4267，说明PC1与四个宏观经济指标高度正相关，而其他主成分仅与部分宏观经济变量高度相关。而且，从表3列示的各主成分的特征根来看，只有PC1对应的特征根的值λ1>1，其方差贡献率达到35.57%，表明选择第一主成分作为宏观经济总体状况的代理变量是恰当的。进一步地，基于主成分法的分析结果，根据公式(14)计算获得反映宏观经济总体状况的综合指数MACRO。

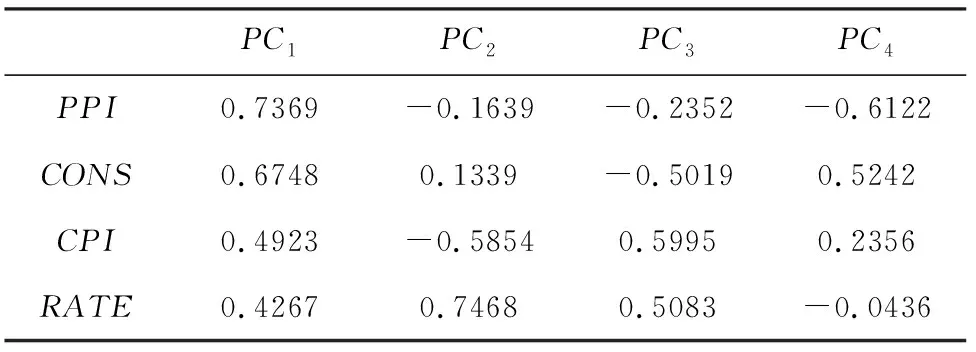
表2 主成分与宏观经济变量间的相关系数

表3 各主成分对应的特征根

纳入PPI、CPI、CONS、RATE的多因子GARCH-MIDAS模型的估计结果分别对应于表4中的模型1-4以及图1中的图(a)-(d)。纳入PC1、MACRO的多因子GARCH-MIDAS模型的估计结果具体见表4中的模型5-6以及图1中的图(e)-(f)。

表4 纳入宏观经济变量的多因子GARCH-MIDAS模型估计结果

综合比较信息准则和似然比函数值发现，总体上看，模型1-6的信息准则AIC和BIC均小于表1所示的单因子GARCH-MIDAS模型，而似然比函数值LLF均大于单因子GARCH-MIDAS模型，表明纳入宏观经济变量的多因子GARCH-MIDAS模型具有比股票市场波动率单因子GARCH-MIDAS模型更好的计量功效。在所有6个模型中，刻画GARCH效应的α+β系数均显著小于1并非常接近于1，根据Engle 和 Rangel[23]的研究，此时条件方差将会以合理的速度收敛于其均值，说明纳入宏观经济变量之后，股票市场高频波动同样具有较好的均值回复效应，宏观经济变量对股票市场高频波动并不产生影响。进一步地，图1所列示的纳入宏观经济变量的GARCH-MIDAS模型的股票市场波动的长期成分与总条件方差的拟合趋势直观地显示，股票市场波动的长期成分与其总条件方差的整体变动趋势高度吻合，意味着纳入宏观经济变量的GARCH-MIDAS模型具有较高的拟合优度。

图1 纳入宏观经济变量的多因子GARCH-MIDAS模型的条件方差与波动性长期成分拟合图

与单因子GARCH-MIDAS模型的估计结果完全一致的是，在1%的显著性水平上，所有模型1-6中的已实现波动率RV的系数均显著为正，说明纳入了宏观经济变量之后，股票市场已实现波动性对股票市场的长期波动依然具有显著的正向放大作用。

从单个宏观经济变量对股票市场波动的长期结果来看，PPI、CPI、CONS从水平值和波动率两个维度均对股票市场波动性产生了显著的长期影响。虽然水平值系数和波动率系数有正有负，但θV的绝对值均远大于θL的绝对值，显示出各宏观经济变量的变动对股票市场波动存在着不同程度的影响，其中波动率对股票市场波动的影响远远大于其水平值对股票市场波动的影响，表明来自宏观经济变量的非预期不确定性冲击对股票市场长期波动的影响远大于宏观经济变量自身的变化。

同业拆借利率波动率对股票市场波动的长期影响不显著，其水平值的影响显著但对应的θL系数值非常小，意味着同业拆借利率的变化不会对股票市场长期波动产生明显影响。虽然利率调整对股票市场产生短期影响效应已经获得孟庆斌等[29]等等研究的证实，但长期内利率调整并不会对股票市场波动产生影响。比较分析模型1-4的估计结果发现，纳入CPI的GARCH-MIDAS模型的θL和θV系数的绝对值最大，表明CPI的水平值及其波动率对股票市场波动的长期成分影响最大，CPI的波动率对股票市场波动的长期成分具有非常显著的推波助澜作用。一方面是因为CPI的变化对消费和生产甚至整个宏观经济均会产生全局性的重要影响，并最终对股票市场波动产生长期影响；另一方面，市场对CPI的预期往往存在很大的不确定性，来自非预期的CPI冲击起到了关键性的作用。

从宏观经济总体状况对股票市场波动的长期影响机制来看，纳入第一主成分和宏观经济综合指数的GARCH-MIDAS模型估计结果基本一致，即θL系数显著为负(第一主成分在1%的显著性水平上显著，宏观经济综合指数的θL系数在10%的水平上显著)且系数的绝对值非常小，表明宏观经济总体状况的水平变化虽然对股票市场长期波动会产生影响，但影响效应非常微弱。θV系数绝对值较大且显著为正值，说明从长期来看，宏观经济的非预期不确定性对股票市场波动产生了显著影响。

(3)宏观经济对股票市场波动的长期动态影响机制

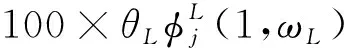
图2 纳入PPI的GARCH-MIDAS模型的滞后期系数变化

从表4模型1关于PPI的RV+XL+XV模型的估计结果来看，PPI水平值的系数为θL=-0.0039，β权重函数中ωL=43.4580，则赋予了滞后1期φ1=85.07%的权重，滞后2期φ2=12.89%的权重，滞后3期以后权重系数几乎为零，表明PPI的水平值当期增加1%，则下一期股票市场波动的长期成分将下降0.33%，滞后2期降低0.05%，第3期后影响几乎为零。PPI波动率的系数为θV=-0.0627，β权重函数中ωV=5.5916，使得权重由滞后1期的φ1=21.60%下降为滞后2期的φ2=17.61%，此后权重逐渐下降，直到15期权重为零，意味着PPI的波动率当期增加1%，将会引起下一期股票市场波动的长期成分下降1.35%，第2期降低1.10%，逐渐下降至第15期以后降为零。从图2可以直观地看出PPI的水平值及其波动率对股票市场长期波动的影响路径。由于生产者价格水平的变化最终要传递给消费者，对企业利润并不会产生显著影响，因此PPI的水平值对股票市场波动影响微弱且持续时间很短。但是，来自生产者价格指数的非预期冲击对生产者信心和生产决策所产生的影响不可忽视，并最终影响到企业利润。因此，来自PPI的非预期冲击对股票市场波动性的影响呈现出递减的负向作用，且具有较强的持续效应。

纳入CPI的RV+XL+XV模型估计结果表明，CPI水平值的系数为θL=0.0096，β权重函数中ωL=8.7039，权重从滞后1期φ1=31.54%迅速下降到滞后6期的φ6=5%左右，在第10期权重几近为零。由此表明，CPI水平值当期增加1%，则下一期股票市场波动的长期成分将增加0.30%，6期后其影响降至0.05%，10期后影响衰减为零。CPI的波动率系数θV=0.1651，β权重函数中ωV=5.9886，权重系数从滞后1期的φ1=22.94%逐渐下降，第15期几乎降为零，意味着CPI波动率的影响显著并持久，从滞后1期1%的变化引起股票市场波动长期成分增加3.79%，至滞后5期仍然为1.5%左右，此后其影响逐渐减小，15期以后逐渐趋近于零。图3显示CPI的水平值对股票市场波动性的影响表现为弱的正向作用，但CPI波动率的增加对股票市场波动性的影响显示出显著的随着滞后期缓慢递减的正向作用。比较图2和图3可知，CPI和PPI两种主要价格指数的波动率影响均显著且具有较强的持久性，但路径恰好相反，并且CPI波动率的影响系数的绝对值要大于PPI波动率的绝对值。消费者价格指数的变化是消费领域和生产领域价格变化的综合体现，所以CPI变化对股票市场波动性明显大于PPI。

图3 纳入CPI的GARCH-MIDAS模型的滞后期系数变化

中国的货币政策传导机制不通畅已经得到学术界的普遍共识。因此，同业拆借利率RATE除了滞后1期的水平值1%的变化引起股票市场波动长期成分微弱地降低了大约0.1%，其波动率对股票市场波动性的影响在长期内几乎均为零。这一结果在图4中可以清楚地看出。宏观经济景气指数CONS是宏观经济景气状况的集中体现，对消费者和生产者的信心产生直接影响。因此，宏观经济景气指数的水平值发生变化时，势必对市场产生直接冲击并引起股票市场长期波动性成分增加，但市场的适应性很快熨平这一效应，显示出很短的持续性。对市场而言，宏观经济景气状况的非预期冲击是一个利坏消息，对股票市场的长期波动产生持久效应。从图5所示的影响系数衰减情况来看，其水平值滞后1期变动将会引起股票市场波动长期成分增加0.3%，滞后2期时该影响就降至0.1%左右，此后的影响几乎接近于零。波动率滞后1期变动将会引起股票市场波动长期成分降低0.32%，但至此以后，其影响缓慢减小，直到24期才降为零，显示出很强的持续性。

图4 纳入RATE的GARCH-MIDAS模型的滞后期系数变化

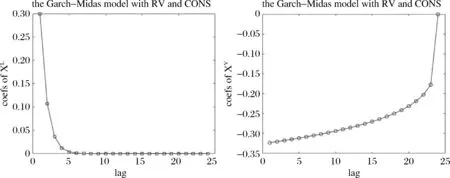
图5 纳入CONS的GARCH-MIDAS模型的滞后期系数变化

反映宏观经济总体状况的指标PC1和MACRO对股票市场波动的长期影响路径和特征基本一致。图6和图7清楚地显示了这一特征。

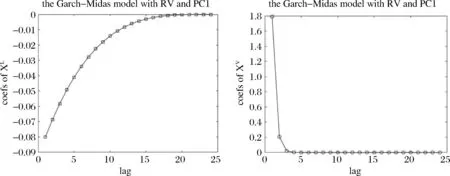
图6 纳入PC1的GARCH-MIDAS模型的滞后期系数变化

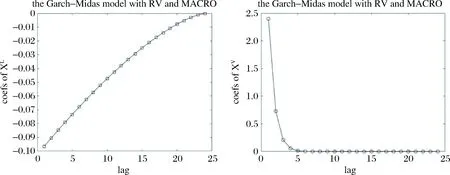
图7 纳入MACRO的GARCH-MIDAS模型的滞后期系数变化

从PC1的RV+XL+XV模型的估计可以看出，PC1水平值的系数θL=-0.0045，β权重函数中ωL=4.5047，赋予滞后1期φ1=17.80%的权重，然后权重系数呈非线性逐渐下降趋势，到第15期权重降至零，说明PC1水平值滞后1期1%的变化引起0.08%的股票市场波动性长期成分的降低，之后逐渐减弱，至第15期影响为零。PC1波动率的系数θV=0.0202，β权重函数中ωV=49.7172，赋予滞后1期φ1=88.67%的权重，2期权重仅为10.17%，5期以后权重接近于零，表明第一主成分PC1波动率增加1%，在滞后1期引致股票市场波动性长期成分增加1.79%，在滞后2期，其影响便下降为0.21%，此后影响快速下降，至第5期几乎衰减为零。

MACRO的RV+XL+XV模型估计结果揭示，MACRO水平值的系数θL=-0.0096，β权重函数中ωL=2.4361，赋予滞后1期φ1=10.05%的权重，然后权重系数呈线性下降趋势，到24期才降为零，意味着MACRO水平值1%的变化降低了0.08%的股票市场波动性长期成分，然后逐渐减弱，至第24期影响降为零，显示了较强的持久效应。MACRO波动率的系数θV=0.0341，β权重函数中ωV=27.8350，赋予滞后1期φ1=70.34%的权重，但权重系数迅速下降，滞后5期降到1%以下，意味着MACRO的波动率增加1%，使得滞后1期的股票市场波动性长期成分增加了2.40%，滞后2期以后迅速下降，从0.73%一直降到滞后5期为0.05%，5期以后的影响几乎变为零。

图6和图7中PC1和MACRO水平值与股票市场波动之间的关系是股票市场波动逆周期性特征的集中体现。即宏观经济繁荣则股票市场波动性小，宏观经济萧条则股票市场波动性大。而且来自宏观经济总体状况的非预期冲击对市场影响很大，以至于引起了股票市场巨大波动，但由于这种非预期冲击具有很大的随机性特征，市场对该新息快速的消化吸收导致这种效应的持续性不强。

4 结语

鉴于股票价格时间序列与宏观经济变量时间序列原始数据的不同频，传统计量模型在处理宏观经济波动与股票市场波动的关系相关问题过程中，由于数据变频处理而容易导致信息失真、模型误设和估计偏误等诸多问题这一客观事实，本文以上证综指日度数据为被解释变量，选取PPI、CPI、宏观经济景气指数和同业拆借利率四个宏观经济变量的月度数据为解释变量，运用GARCH-MIDAS模型从水平值和波动率两个维度实证分析了宏观经济变量对股票市场波动的长期动态影响。同时，为了系统考察宏观经济总体状况对股票市场波动的影响，本文进一步运用主成分分析获得第一主成分并构建了一个宏观经济综合指数并进行了实证分析。研究结论如下：

首先，单因子GARCH-MIDAS模型和多因子GARCH-MIDAS模型的实证结论均表明，中国股票市场短期波动呈现出显著的均值回复效应和波动性集聚效应，股票市场自身的已实现波动率显著加剧了股票市场的长期波动性。该结论与现有相关文献的结论一致，揭示了GARCH-MIDAS模型在中国证券市场中的适用性。

其次，PPI、CPI、宏观经济景气指数从水平值及其波动率两个维度对股票市场波动性均有显著的长期影响。其中PPI在两个维度上均呈现出负向影响效应，CPI则具有双维度的正向放大效应，宏观经济景气指数的影响相对复杂，其水平值对股票市场长期波动性成分具有放大效应，波动率则具有负向影响。同业拆借利率的波动率影响不显著，其水平值的影响显著但影响程度很微弱，意味着同业拆借利率的变动几乎不会对股票市场长期波动产生显著影响。而且，PPI、CPI、宏观经济景气指数的波动率对股票市场波动的长期影响效应显著大于其水平值。其中CPI对股票市场波动的长期成分影响最大，PPI的影响次之。虽然单个宏观经济变量对股票市场长期波动性具有不同的影响机制和影响效果，但纳入宏观经济第一主成分和宏观经济综合指数的多因子GARCH-MIDAS模型获得的结论一致，即宏观经济总体状况的水平值对股票市场波动性的影响作用虽然显著但相对微弱，宏观经济总体的波动率对股票市场长期成分的波动具有显著的正向放大作用。

再次，单个宏观经济变量、表征宏观经济总体状况的第一主成分和宏观经济综合指数对股票价格长期波动具有各自不同的动态影响机制。PPI的水平值对股票市场长期波动性具有瞬时的负向影响效应，显著作用一期以后迅速衰减为零，PPI的波动率对股票市场长期波动性起到了负向作用具有较强的持续性。CPI的影响路径较之于PPI恰好相反，CPI的水平值和波动率对股票市场长期波动性均表现为随滞后期缓慢递减的正向放大效应，具有较强的持久性。宏观经济景气指数CONS的水平值对股票市场长期波动性成分的持续效应小，但其波动率则呈现出很强的持久效应。同业拆借利率的持续性几乎可以忽略。度量宏观经济整体运行情况的第一主成分和宏观经济综合指数具有大致相同的影响机制。宏观经济总体水平值的变动对股票市场长期波动性呈现出很强的持续效应，其波动率变动对股票市场长期波动性的影响持续时间相对较短。

在当前中国经济正处于结构性减速的经济背景下，来自国内国外的不确定性因素明显增加，“稳增长、调结构、防风险”已经成为当前乃至未来一段时间中国经济工作的核心。学术界关于经济周期与股票价格之间的关系的一般共识是“股票价格具有顺周期性，股票价格波动具有逆周期性。”本文关于宏观经济对股票市场长期波动影响机制的研究结论实际上是对这一观点的深化：生产、消费、金融市场等宏观经济的变化对股票市场价格的确起到基础性的作用，但这种作用有限；更重要的是来自宏观基本面的非预期冲击对股票市场价格波动产生了重要影响。

但宏观基本面的非预期冲击对股票市场价格波动的作用机制是什么？限于篇幅，本文并没有深入研究，也是一个暂新的研究方向，今后可以从经济不确定性(包括经济政策不确定性)、投资者情绪等视角，通过DSGE建模等方法展开深入的理论研究。