基于遗传算法的装备采购决策优化研究

雷绍雍，刘靖旭

(1.战略支援部队信息工程大学研究生院，河南 郑州450001；2. 战略支援部队信息工程大学地理空间学院，河南 郑州450001)

1 引言

装备采购，指军队选择购买军事装备的有关活动。它是装备建设的重要内容，是装备从提出需求到形成作战能力之前的整个生成过程中的最后一个环节。这项工作的成败，直接关系到装备购置费能否发挥其应有的效益，关系到部队装备的质量，在军队现代化建设中占有重要的地位[1]。许多装备采购决策问题都具有多目标、多约束、规模较大、结构复杂等特点，传统的依赖决策者阅历、知识和偏好的经验型决策已经不能满足装备采购的需要，必须分析采购决策的特点，利用信息手段、智能算法构建决策模型，对信息繁杂、内容丰富、目标多元的装备采购决策问题作出精确判断和科学定量，运用智能优化算法对装备采购决策问题进行求解，实现装备采购保障的优化决策。

目前，在装备采购决策方面，国内外学者有一定的研究，主要可以分为以下几类：一是线性权重法，它的思想是按照一个选择准则配备一个权重，各项选择准则的得分与相应权重的乘积的和是该供应商定量结果，最后，对各供应商定量选择结果进行比较得出最佳供应商。常见的线性权重法有德尔菲法、熵值法、分类比较法、蒙特卡洛法等。比如文献[2]、[3]都运用了德尔菲法对装备采购决策进行了分析研究，文献[4]Gregory 运用分类比较法给出供应商每个准则的基本判断，然后计算供应商的总积分；文献[5]、[6]采用的蒙特卡洛法,建立了多属性决策模型,并给出了求解方法。此方法局限性在于只能解决单目标决策问题，对于多目标决策想应用此方法必须先转化为单目标决策问题，而上述研究并没有给出多目标决策如何转化成单目标决策的方法。二是综合成本法，主要内容是对符合条件要求的供应商的采购报价进行比较，价格低的供应商为最佳供应商。比如Timmerman[7]通过计算各分项占总成本的百分比，来确定最终供应商；Roodhooft 和Konings[8]则提出了ABC成本法，通过明确采购的主要矛盾，分清重点与一般，有区别地计算直接成本和间接成本，最终对比总成本来确定供应商。而在现实装备采购中并不仅仅追求低成本，决策属性中装备安全性、可靠性以及装备运达的及时性等要素同样相当重要，所以成本法对于装备采购决策并不完全适应。三是数学规划法，包括线性规划、多目标规划、整数规划，混合规划等，其局限性在于对问题性质有着一些特殊要求，大大限制了方法的应用范围，而且决策变量局限于一个连续的空间内，当出现非凸集时不一定能求得最优解。如文献[9]提出了模糊随机动态规划研究模型，利用随机数模拟方法进行求解；文献[10]针对多属性多阶段决策问题，运用极大熵原理建立多目标优化模型，利用拉格朗日乘子法进行求解；文献[11]利用临界值策略给出了凸情形下该类问题的一种解法。

装备采购决策核心就是供应商评选，这是一个多准则决策问题。文献[12]采用模糊分析法对医疗设备供应商进行排序，使其与理想解相似。文献[13]建立了一个犹豫模糊集模型用于选择供应商。文献[14]利用三角模糊信息对供应商绩效进行了评价。文献[15]采用改进的直觉模糊优次排序方法解决了供应商选择问题。文献[16]采用一种综合的多准则决策方法对绿色供应商进行评价。文献[17]分析了供应商选择的失败风险、数量和业务量折扣。文献[18]提出了一种新的具有两级准则的混合MCDM方法来寻找最优供应商。文献[19]提出了一种结合AHP和TOPSIS的混合模型来选择最合适的供应商。文献[20]提出了不同决策目标下受资金约束零售商在采购策略上的差异性。文献[21]提出了基于商业信用的供应商选择策略。文献[22]针对集团采购供应链中信息共享的协调作用展开研究，从信息共享角度提出供应商选择的优化策略。

本文将装备采购问题转化为指派问题，构建多约束条件下的多目标模糊指派模型，该模型能够很好的弥补上述方法的局限性。近年来，智能算法常被用来解决多目标决策优化问题，由于遗传算法具有群体搜索的特性，具备自组织、自适应、可扩展和自学习性等特点，以目标函数作为搜索信息，不需要详细的函数解析式，所以本文选择一种改进的遗传算法对该模型进行求解，并给出了算例及仿真示例结果。

2 问题描述及数学建模

实际装备采购活动可以抽象为：从m个装备供应商采购n种装备(m≥ n)，考虑L个约束条件(比如采购成本不能超过采购预算；采购任务有时限要求等)，实现P个目标(如价格低廉，可靠性高，安全性好等)的综合效益最大问题。此类问题其实可以归为多约束条件下的多目标模糊指派问题[23-24]。

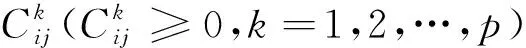
(1)

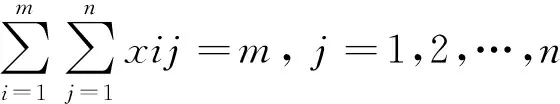
xij=0,1i=1，2，…m;j=1，2，…，n

j=1，2，…，n；k=1，2，…，p

(2)

对于多目标优化问题，一般采用的方法是将目标进行整合转化为单目标最优化问题，具体步骤如下：

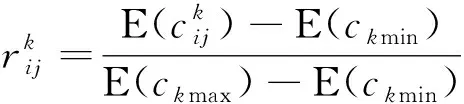
(3)

(4)

上式中，E(ckmax)和E(ckmin)表示矩阵E(Ck)中的整体期望值的最大和最小值。从而得到在目标k下属性值对优的隶属矩阵：

(5)

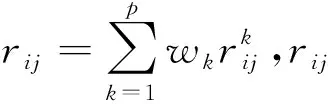
(6)

至此，多目标非平衡指派问题数学模型就转化为：

i=1，2，…，m；j=1，2，…，n

(7)

j=1,2,…,n

(8)

求解非平衡指派问题的数学模型一般将其等价转化为平衡指派问题进行处理，也就是添加m-n件虚拟装备，凑成m件装备。虚拟装备是不存在的，其产生的效益值为0，因此其不会改变问题的实质。扩展后的合成效益矩阵和约束矩阵分别变为Q、S，则：

对应的模型就变为：

(9)

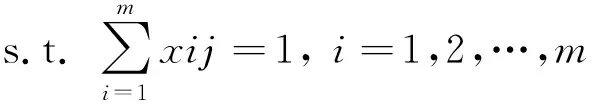
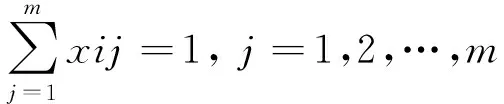
xij=0,1，i,j=1,2,…m

3 基于遗传算法的问题求解

3.1 遗传算法的描述

遗传算法[25-27]是将问题的解编码为“染色体”，组成编码的元素称为“基因”。在算法迭代过程中，按照“适者生存”的规律，选取适应度高的染色体进行复制，并对它们进行杂交和变异的操作，产生出生存能力更强的新染色体群。通过这样不停反复的进化，直到产生出生命力最强的染色体产生为止，这个生命力最强的染色体就是问题的最优解。

遗传算法执行的基本流程如下：

Step1：编码。

Step2：种群初始化。

Step3：适应度计算。一般将目标函数值作为个体的适应度函数。

Step4：选择。计算种群中每个个体的适应度，选取其中适应度较高的一些个体作为种群。

Step5：交叉。在种群个体之间进行交叉操作，得到新一代种群。

Step6：变异。在新群体中选取少量个体进行变异操作。

Step7：判断是否满足终止条件，满足则输出最优解，否则跳到执行Step3。

图1 算法基本流程图

3.2 遗传算法设计

遗传算法本身也有一些缺陷，主要表现为快要接近最优解时在最优解附近左右摆动，收敛较慢；容易得到结果是局部最优解而不是全局最优解。结合实际问题，本文对基本遗传算法进行了优化改进，

详细步骤如下：

第一步：编码。这里通过符号对基因进行编码，染色体串长度为需采购的装备套数m,每个基因就代表一个目标，等位基因是提供装备的供应商，这样每一个染色体就代表一种分配方案。例如，某染色体串为“423615”表示共需采购6套装备，第1套装备从供货商4采购，第2套装备从供货商2采购，依次类推其余目标。

第二步：种群的初始化。首先确定种群规模和最大遗传代数，而后采取适当的方法确定符合要求的初始种群。

第三步：适应度值计算。针对装备采购的遗传算法模型，适应度值为每个基因个体矩阵与效益矩阵q、s中相对应单元乘积的最大值，其中基因个体矩阵中基因值为行标、基因位为列标。

第四步：选择。每次一个代内求得的最优解，可以直接进入下一代的群体中，其余个体按照“轮盘赌”方法进行选择，并参加交叉与变异。个体的选择概率Pi为：

(10)

式中，fi表示适应度,i=1，2，…，n。

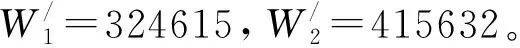
第七步：按照终止条件判断输出结果，如果满足终止条件则输出最优解，否则跳到第三步。

4 仿真验证

4.1 示例仿真

按照演习任务需要，急需采购三种装备，其中A装备83套，B装备31套，C装备52套；从装备采购信息平台里选出5家优秀供应商参与此次竞标采购，各公司关于三种装备单套报价如表1；同时，根据各供应商竞标文件的陈述，综合考虑供应商规模、资质、业界地位以及产品市场占有率等各方面因素，由专家组以模糊数的形式给出从各供应商采购装备的时间、质量、性能如表2、3、4所示。要求此次采购任务48小时内完成，采购金额不能超过500万，力求最佳质量和性能，假定价格、时间、质量和性能等权重。

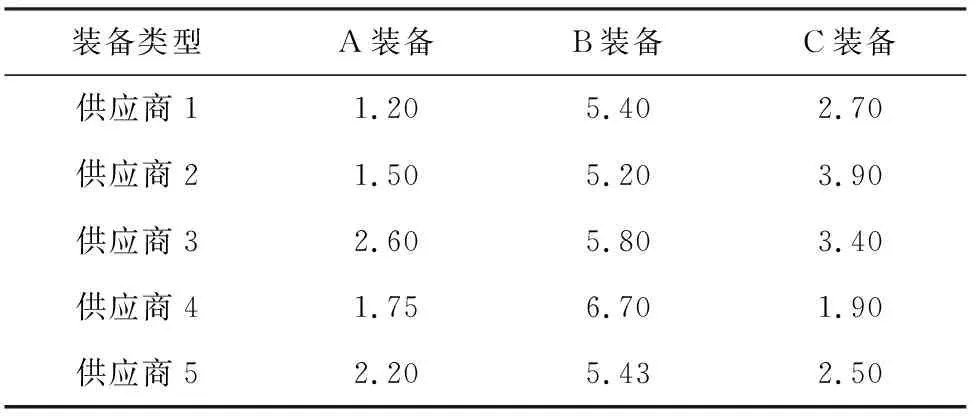
表1 供应商对各装备的报价(单位：万元/套)

表2 供应商送达装备的耗时(单位：小时)

表3 供应商提供装备的质量(百分数表示)

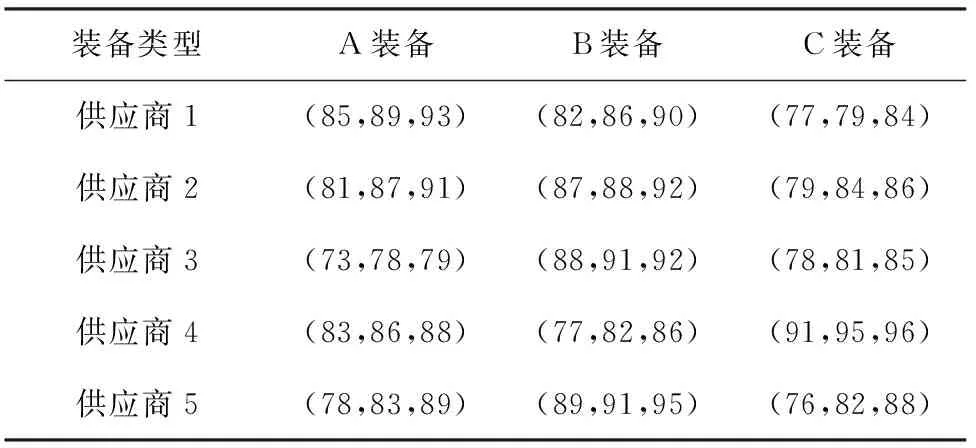
表4 供应商提供装备的性能(百分数表示)

设定种群规模为50，最大遗传代数为50，用MATLAB2016进行求解，得出目标从第五代开始收敛于1.007，最优解为34251，即从供货商3采购A装备，从供货商4采购B装备，从供货商2采购C装备，其余2个供应商为虚拟任务，无现实意义。仿真结果见图2。

图2 仿真结果图Fig.2 The initial distribution map

由仿真结果可以看出，仅用了5次迭代，耗时0.237秒，就可以得出函数最优解，证明遗传算法在上述装备采购问题中应用效果较好，具备收敛速度快和较好的全局搜索能力，验证了该算法的有效性和实用性，能够满足决策的实时性要求，可以为装备采购决策提供依据。

4.2 算法对比实验

匈牙利算法是求解指派问题的一种经典算法。本实验针对上述示例，逐步增加供应商数量(m)和采购装备种类(n)，分别运用遗传算法和匈牙利算法进行求解，并作出对比。

实验中包含20个示例，实验环境为一台3.20 GHz AMD Ryzen 5 1600 Six-core Processor处理器、16GB内存的计算机，MATLAB2016软件。算法实验结果如表5。从表中可以看到，遗传算法找到最优解的效率总是优于匈牙利算法，而且随着供应商数量和采购装备种类的不断增加，匈牙利算法所需的时间呈指数增长，而遗传算法的求解时间远远小于匈牙利算法，这充分证明了遗传算法的优越性。因此，针对本文所提问题及模型，遗传算法的求解效率要远远优于匈牙利算法。

表5 指派问题实验结果

5 结语

本文根据装备采购问题，构建了多约束条件下的多目标模糊指派模型。同时,详细阐述了数学建模过程，并设计出遗传算法对该模型进行求解。最后通过案例验证和算法对比实验，证明该算法收敛速度快，容易得出最优解，在实际问题中应用效果较好，对装备采购决策优化具有较高实用价值，同时该模型对构建与求解其它指派问题，也有一定的参考价值。