考虑定价和需求关系的供应链网络优化研究
胡鸿韬,边迎迎,郭书源,王帅安,严 伟
(1. 上海海事大学物流工程学院,上海 201306;2. 香港理工大学物流及航运学系,香港 999077)
1 引言
经济的不断发展使得当今世界的竞争变成了供应链之间的竞争。供应链网络是由供应链中的制造商、供应商、零售商以及消费者所构成的网络[1]。在现有的供应链网络研究中,一般假设产品的需求量是已知的。但是,在产品质量、市场环境等条件相同的情况下,需求量在很大程度上是由产品价格决定的。如果价格超过消费者的估值,即使高质量的产品也很难打开市场,进而影响企业利润。因此,在供应链网络研究过程中考虑产品价格对消费者需求的影响具有理论意义和实际价值。
当前,供应链网络优化问题已经被国内外许多学者研究。Fattahi等[2]用模拟退火算法研究具有产能限制的动态供应链网络设计问题。陈芳等[3]和郭传好等[4]研究了乳制品的供应链网络设计及成本优化问题。王熹徽等[5]研究了社会损失最小化的救灾物资供应链网络设计优化问题。也有部分学者研究了供应链网络的复杂性对消费者需求的影响。通过研究供应链的复杂性和运作过程的不确定性,万仲平等[6]指出激烈和复杂的市场竞争导致了消费者需求的不确定性。
此外,针对存在竞争关系的供应链网络结构设计问题,Zhang Shuzhong[7]提出价格是影响消费者是否选择产品或服务的唯一因素。Shen[8]认为制定合理的价格是保证市场竞争力的有效手段。Ahmadi-Javid和Ghandali[9]也指出供应链网络中价格敏感型消费者的需求取决于产品价格。之后的学者在研究动态的供应链网络问题中考虑了产品的价格和需求量。例如,Ahmadi-Javid和Hoseinpour[10]在考虑价格敏感型需求的基础上研究了多商品供应链网络优化问题,并对配送中心的容量限制进行分析。Talluri 和Van Ryzin[11]提出不同的产品,其定价和生产量不同,并且其价格会随时间而变化。然而,在合理地引入价格和产量决策的同时,对需求的描述是及其困难的。例如,杨道箭等[12]将需求用一个确定的随机函数来表示。Sahling和Kayser[13]假设在动态供应链网络中,消费者需求服从正态分布(参数已知),根据产品生产量的变化解决未满足的订单量和累计的库存量。徐家旺和黄小原[14]采用已知确定概率的离散情景并结合鲁棒性来描述供应链网络中需求的不确定性。然而以上并没有动态的描述供应链网络中的价格和需求的关系。
针对价格敏感型消费者,本文引入价格-需求函数来动态描述产品价格变化对消费者需求的影响。由于动态定价会导致数学模型的非线性,对于模型中的非线性部分,将价格离散化是最常见的处理方式[9-11],例如,Fattahi等[2]为了便于求解复杂供应链网络优化问题,在引入价格-需求函数后将定价水平离散化,但由此增加的整数决策变量,在一定程度上会降低模型的求解规模和求解速度。Du Yuquan等[15]在研究考虑油耗和排放的泊位安排问题时,用二阶锥规划求解非线性问题。Wang Shuaian等[16]研究班轮运输中在需求对运输时间敏感的前提下集装箱船的排班问题,针对非线性项用二次曲线和分支定界法求解。
综上,本研究构建了考虑定价和需求关系的供应链网络优化模型,并通过不同规模的算例验证了模型的可行性和有效性。首先在供应链网络优化设计中引入价格—需求函数,刻画产品定价和消费者需求的关系。由于引入价格-需求函数,目标函数中产生非线性项,使用外部近似法将其近似成有限条切线并添加线性约束,使其可以用数学商业优化软件求其最优解,确定产品的定价和需求。
本文余下部分结构如下:第二部分对研究的问题进行描述,并对相关符号进行说明;第三部分建立考虑定价和需求关系的供应链网络优化模型;第四部分使用外部近似法对目标函数中的非线性项进行处理,使得可以直接求解,并通过不同规模的算例验证了模型的可行性和有效性;相关的结论在第五部分展示。
2 问题描述及符号说明
2.1 问题描述
如图1所示,本文针对价格敏感型消费者,建立了一个由单一制造商、多个仓库、单一顾客群组成的三级供应链网络。在该供应链网络中,考虑单产品在多周期内进行生产运输。制造商生产产品且全部运至仓库,产品从仓库直接运至消费者进行销售。消费者端引入价格-需求函数[2]描述产品定价和需求量的关系,从而在对定价进行决策的同时动态描述需求的不确定性。
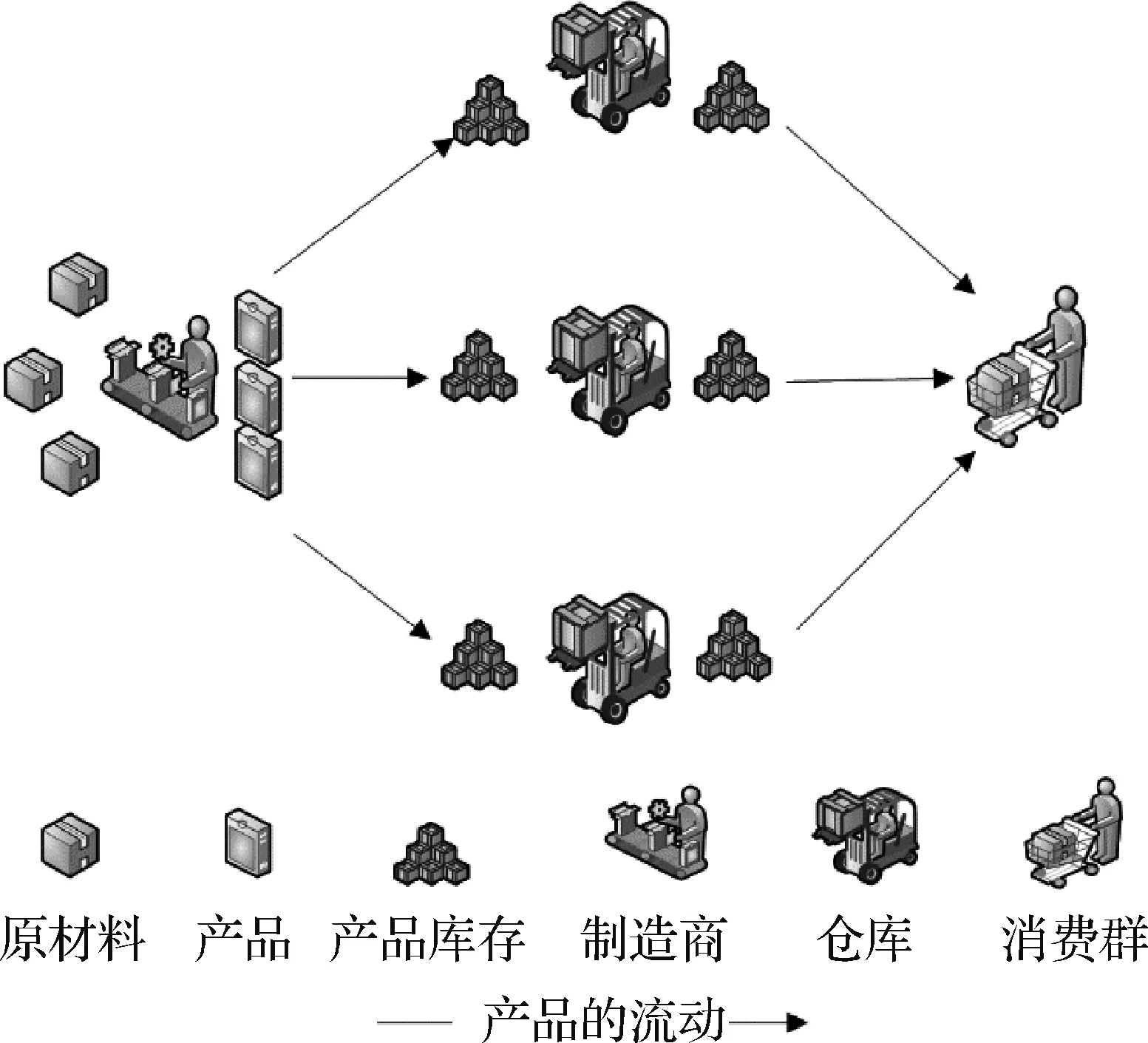
图1 供应链网络结构图
2.2 符号说明
集合:
T周期的集合,t∈T,T={1,2,…,|T|}
W仓库的集合,w∈W
参数:
Rw仓库w投入运营的固定成本
Gt周期t内原材料的单位采购成本
Mt周期t内制造商生产单位产品的生产成本
It周期t内制造商处原材料的单位库存成本
Iwt周期t内仓库w中单位产品的库存成本
Vwt周期t内制造商将单位产品运往仓库w的运输成本
Cwt周期t内仓库w将单位产品运往顾客的运输成本
A单位产品需要的原材料数量
h0期初原材料的库存量
hw0期初仓库w中产品的库存量
Hmax制造商处原材料的最大库存水平
Ωmax制造商的最大生产能力
Kmax制造商车队运输产品的最大运输能力
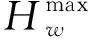
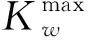
a价格-需求函数中的参数,当价格小于a时,需求为D
b价格-需求函数中的参数,当价格大于b时,需求为0
D需求的最大值
决策变量:
pt周期t内产品的价格
dt周期t内产品价格确定后的需求量
yw0-1变量,当且仅当仓库w投入运营时为1,否则为0
qt周期t内,制造商处对原材料的采购量
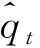
ht周期t内,制造商处原材料的库存量
hwt周期t内,仓库w处产品的库存量
kwt周期t内,制造商将产品运往仓库w的运输量
swt周期t内,仓库w将产品运往顾客群的运输量
3 数学模型
3.1 基本假设
(1)不考虑供应链网络中同级间的竞争。
(2)制造商所需的原材料是单一的,且不考虑原材料采购的提前期。
(3)采用(t,Hmax)策略进行原材料的补货,即周期t检查库存并把现有库存补充到最大库存水平Hmax。
(4)生产的产品只需满足一种类型的顾客需求。
3.2 价格-需求函数
一般来说,顾客的需求量是与产品当前定价相关的,在此引入价格-需求函数[2](图2)来描述其间的关系。即产品价格pt小于a时需求dt为最大值D;产品价格在a和b之间时,需求与价格线性相关且随着价格的变大而变小;价格大于最大值b时需求为0。
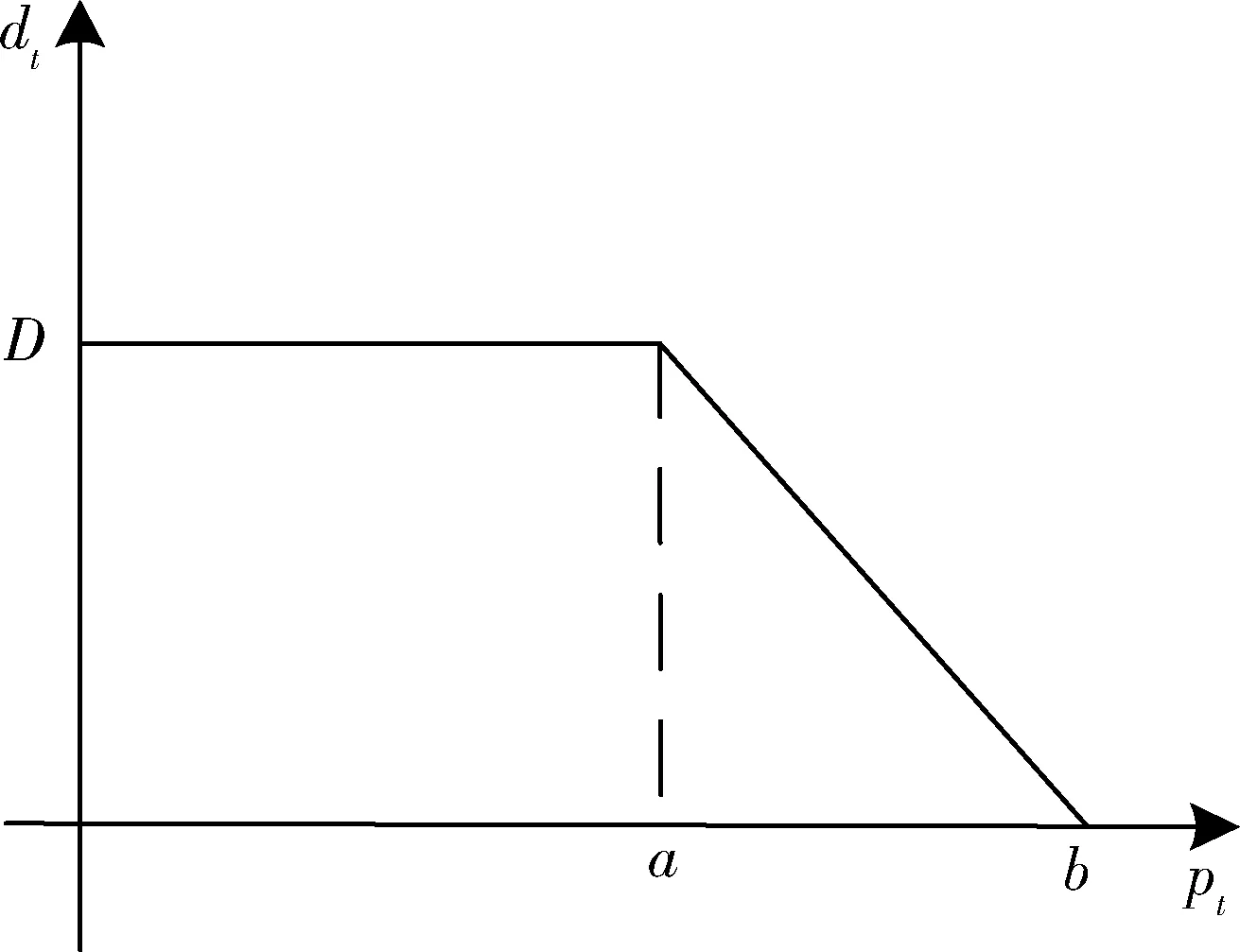
图2 价格-需求函数
根据图2,可以写出价格-需求函数的关系式:
(1)
3.3 数学模型
本文以最大化供应链总利润为目标、以生产量和定价为决策变量,建立了混合整数非线性规划(MINLP)模型。由于产品生产量影响顾客需求量,制造商处需要保证原材料的库存确保产品的生产。对于企业仓库而言,它的选择和运营不仅需要考虑多方面的因素,也需要投入大量的人财物。因此仓库的选择会在整个计划期初进行决策且只决策一次。因为价格在不同周期可能不同,而需求会受价格的影响,所以需求量也会相应发生动态变化。模型[P]如下:
(2)
s.t.qt+ht=Hmax∀t∈T
(3)
(4)
(5)
kwt≤Kmax·yw∀w∈W,∀t∈T
(6)
(7)
(8)
(9)
(10)
(11)
(12)
hw(t-1)+kwt=hwt+swt∀w∈W,∀t∈T{1}
(13)
hw0+kw1=hw1+sw1
(14)
yw∈{0,1}
(15)
(16)
目标函数(2)表示供应链网络的总利润。其中,第一项表示销售产品的总收入;第二项为仓库的建设成本;第三项表示原材料的采购成本;第四项表示制造商的生产成本;第五项表示制造商处原材料的库存成本;第六项表示仓库中产品的库存成本;最后两项表示产品的运输成本。约束(3)表示任意周期t内的原材料采购量。约束(4)表示制造商生产的产品全部运至下一级仓库w中。约束(5)为产能约束,表示制造商的生产水平不超过它的最大生产能力。约束(6)表示产品由制造商到仓库w的运输量不能超过它的最大运输能力。约束(7)表示仓库w中产品的库存量不能超过它的最大库存能力。约束(8)表示产品由仓库w到消费者的运输量不能超过它的最大运输能力。约束(9)表示从仓库运输产品的量要满足消费者的实际需求。约束(10)是价格-需求函数表达式。约束(11)和约束(12)表示产品生产的流平衡。约束(13)和约束(14)表示产品运输的流平衡。约束(15)和约束(16)阐明了0-1变量和非负变量的数值定义。
4 求解及数值分析
4.1 目标函数近似线性化
因为[MINLP]中目标函数是连续函数,所有的约束都是线性的且都是“≤”、“=”和“≥”连接的,没有“<” 和“>”约束,所以[MINLP]的可行域是闭的。由于约束(10)(16)的限制,所以[MINLP]的可行域是有界的。因此,可行域是一个紧集。又因为当所有的决策变量为0是问题的一个可行解,所以可行域非空。即,[MINLP]存在最优解。针对目标函数中存在的非线性项ptdt,现有的商业规划求解软件(如CPLEX)无法直接求解。所以本文使用外部近似法把非线性项转化为线性项并添加线性约束求解。
定义Pt为周期t内的收入,即Pt=pt·dt,由约束(10)可知:
(17)
模型[P]变为[P1]:
(18)
s.t. (3)-(9),(11)-(17)
由于函数Pt在[a,b]是一个凸函数,此时可以使用外部近似法对函数Pt进行近似。
由公式(17)可知,当pt∈[a,b]时,函数Pt是非线性的,所以只需对[a,b]上的曲线进行近似。函数Pt在[a,b]上存在以下两种情况:
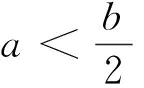
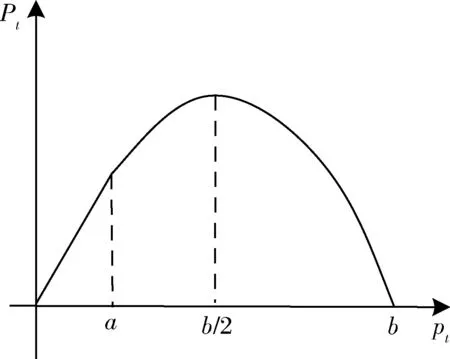
图3 时的收入函数
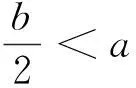

图4 时的收入函数
下面本文将以第(1)种情况为例对曲线进行近似。
由于函数Pt是一个凸函数,此时可以使用外部近似法对函数Pt进行近似。对∀pt∈[a,b],用线段近似Pt并控制其近似误差,设计算法生成分段线性函数。定义公差ε,定义Ψ为切线集合,ψ={1,2,…,|Ψ|}。切线表达式为:rtψ×pt+etψ,其中,rtψ表示切线ψ的斜率,etψ表示切线ψ的截距。那么,分段线性近似函数可表示为:
(19)
(20)
综合公式(19)(20)可得:
Pt≤rtψ×pt+etψ, ∀t∈T,∀ψ=1,2,…,Ψ
(21)
因此,模型[P1]可以写成[P2]:
(22)
s.t. (3)-(16),(21)
由于CPLEX的特长是求解混合整数线性规划模型。经过转换,虽然约束数量有所增加,但是增加的约束仍然是“≤”连接,且目标函数及约束的性质并没有发生改变。故由线性处理前存在最优解可知,通过外部近似法处理后的模型[P2]仍然存在最优解。
为了便于理解,分段线性近似函数的切线生成步骤如下,图5(以t期产生的4条切线为例)所示:
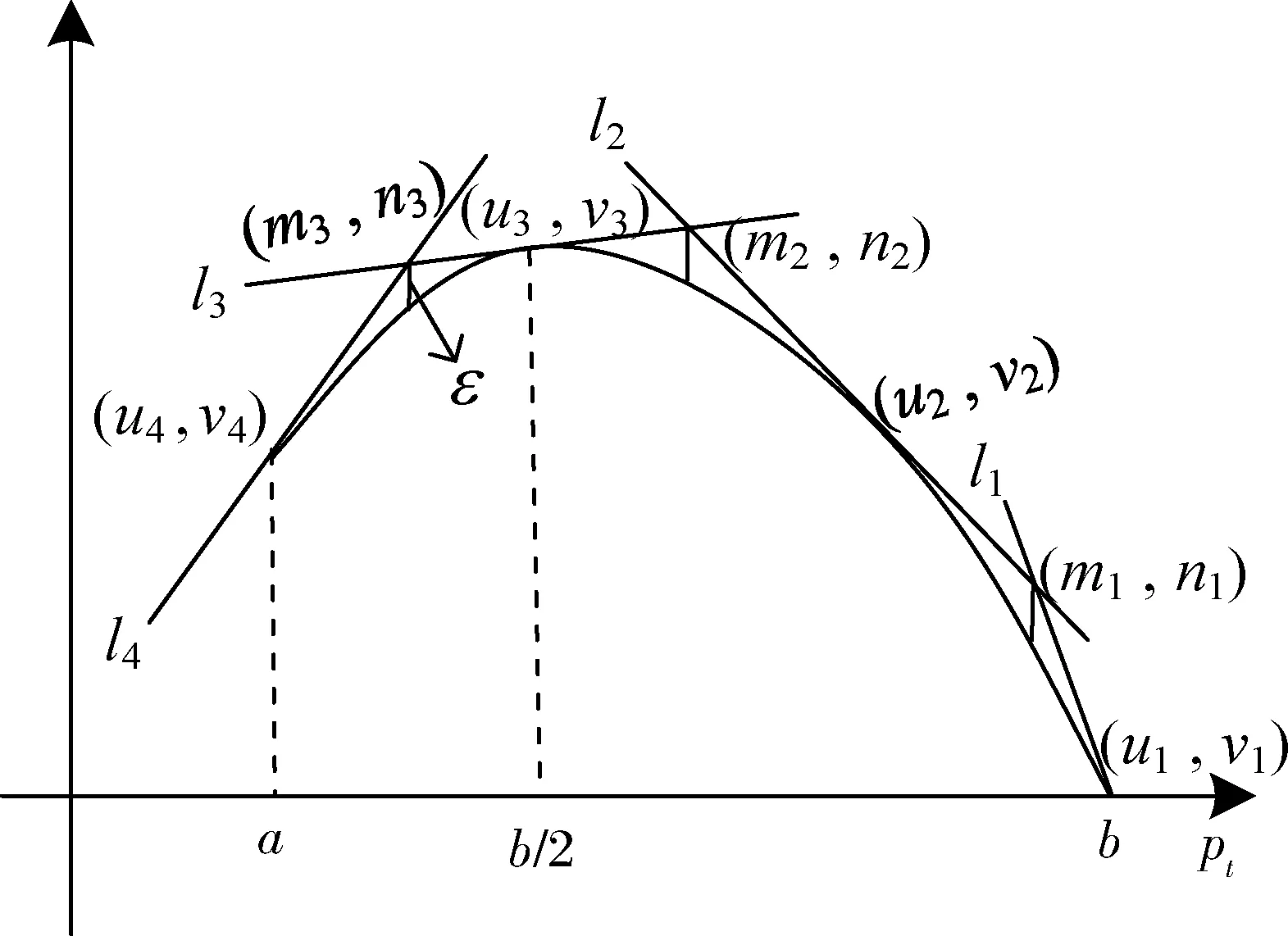
图5 t期切线生成步骤
Step 0:设置切线ltψ和曲线Pt之间的误差ε,定义切点的坐标为(utψ,vtψ),切线交点即误差值点的坐标为(mtψ,ntψ);
Step 1:令ψ=1,此时切点(utψ,vtψ)=(b, 0),过点(utψ,vtψ)作曲线Pt的切线ltψ;
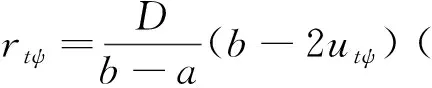
Step 3:令切线ltψ和曲线Pt之间的差值为ε,得出误差值点(mtψ,ntψ),其中ntψ=rtψ·mtψ+etψ;
Step 4:判断mtψ≥a,若是,令ψ=ψ+1进入Step 5;否则计算结束,输出一组直线的斜率和截距;
Step 5:过点(mt(ψ-1),nt(ψ-1))作曲线Pt的切线ltψ,跳转到Step 3;
4.2 数值分析
为了证明前面所建模型和算法的有效性,借助计算机(12 GB,i7-4790,3.60 GHz)用数学规划求解软件CPLEX(12.5.1)分别比较不同规模和不同误差下的求解效率。参数设置和求解结果分别见表1和表2:
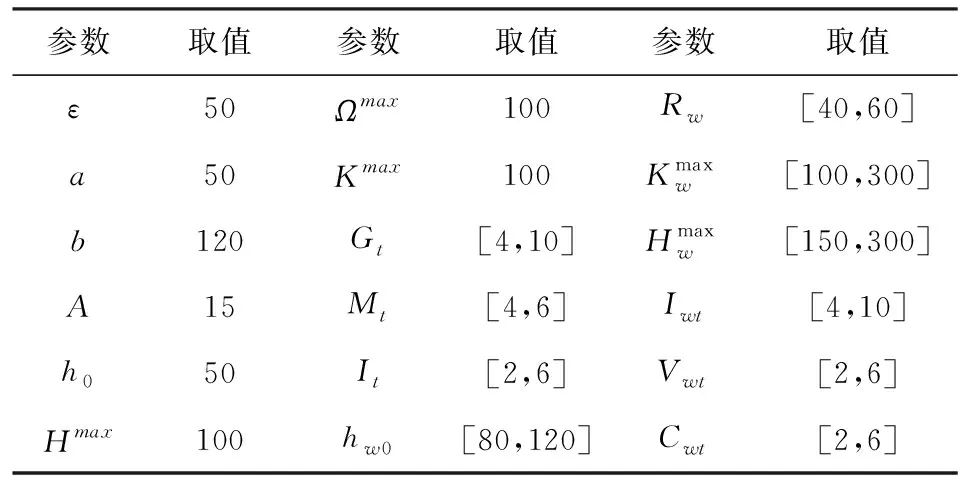
表1 参数设置
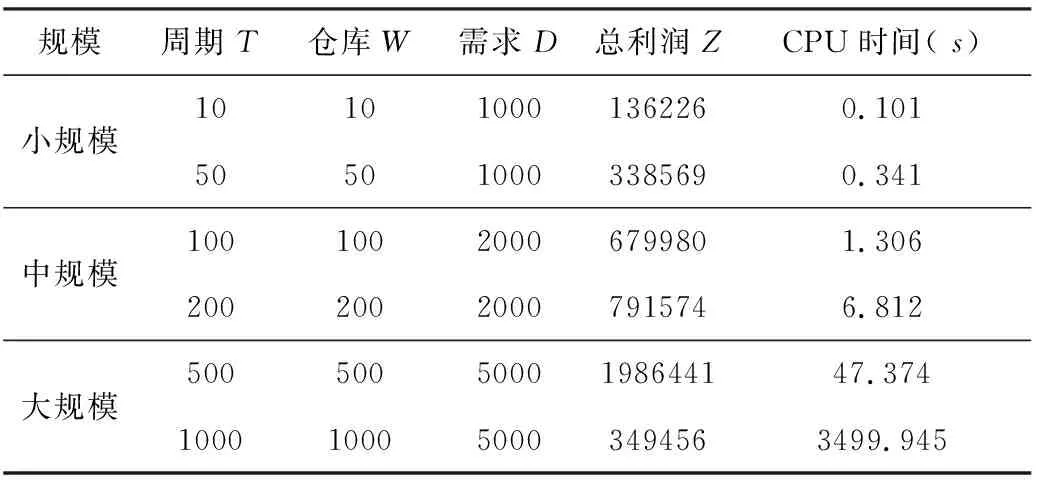
表2 不同规模算例求解结果
通过比较我们可以看出,算法在求解大规模情况时,虽然时间明显加长,但仍可以有效地解决问题。
此外,通过改变误差ε的取值,对同一规模观察求解时间的变化。当T=50,W=50时,不同ε值对求解结果的影响如表3所示:
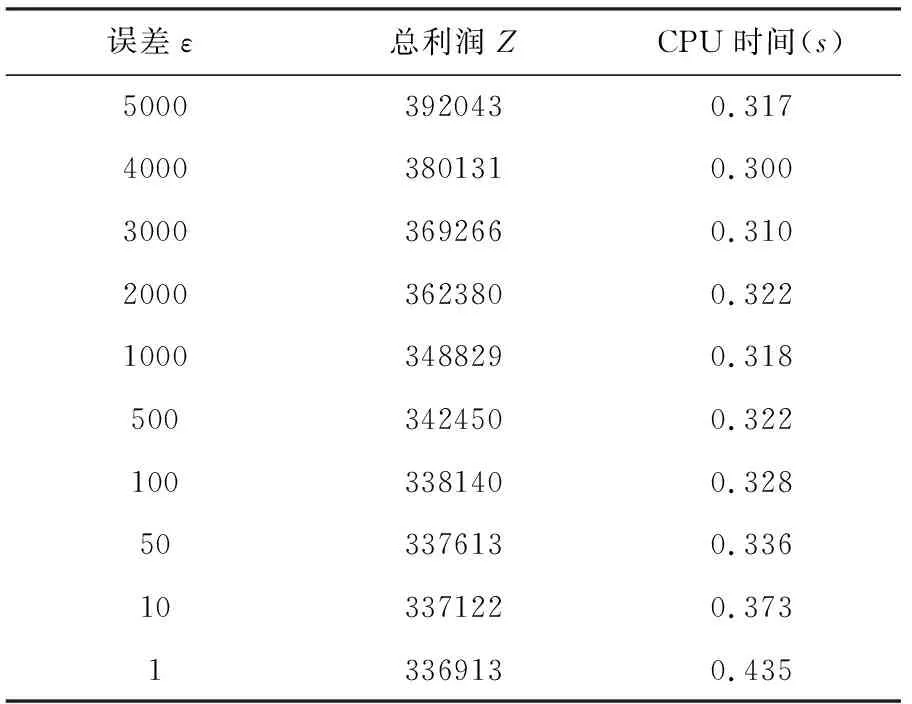
表3 误差值灵敏性分析表
通过表3可以得到:随着误差值ε的逐渐减小,总利润变得越来越小,求解时间不断增加。
5 结语
本文构建了一个价格与需求相关的三级动态供应链模型。该模型采用(t,Hmax)库存策略,以价格敏感型消费者为中心。根据模型非线性的特点,用外部近似法把非线性项转换为线性项。最后通过算例给出了模型的应用并对切割的误差值进行灵敏性分析。可以得到以下结论:(1)文章所建立的模型和求解方法可以有效的解决此类供应链的问题,也可以求解大规模问题;(2)在利用外部近似的方法求解模型时,不同误差值的设置对求解的结果和速度影响较大,误差值越小,求解的速度越慢,精度越高。因此,本研究不仅为此类供应链确定合理的价格提供了借鉴和帮助,还有效地指导供应链网络中的企业权衡其成本和收益,提高顾客的满意度。
此外,本文的研究也存在一定的不足之处,例如,假设生产的产品只需满足一种类型的顾客需求,而现实生活中顾客的需求通常多种多样,这就要求供应链可以提供多种类型的产品。再者,大规模算例的求解时间明显变长,可以进一步设计相关算法提高求解效率。

