资产泡沫、技术创新与经济增长

王升泉，陈浪南，刘人豪

(1.中山大学国际金融学院，广东 珠海 519082； 2.中山大学岭南(大学)学院，广东 广州 510275；3.拉夫堡大学商学院，莱斯特 英国 LE11 3TU)

1 引言

“新常态”下我国经济的基本特征之一是经济增长动力的转换，即由过去长期依赖的积累资本与大规模劳动力的模式向技术创新与人力资本提升的模式转变[1]。如何促进技术创新成为政策制定者和学术界广泛关注的话题，创新被认为是发展的第一动力。与此同时，经济泡沫化构成了我国经济的另一个缩影，资产价格的迅速上涨引起了政策当局关于泡沫触发系统性金融风险的担忧[2]。在此背景下，资产泡沫是否可以通过技术创新对经济增长产生影响是个值得深入研究的话题。

纵观文献，资产泡沫的经济增长效应的研究经历了从负效应到正效应的转变过程。Tirole[3]首先研究了资产泡沫产生的条件。为研究资产泡沫的经济增长效应，学者们开始将标准的经济增长模型与Tirole[3]的模型结合。认为泡沫对经济增长不利的有以下代表性文献。Saint-Paul[4]基于新古典的增长模型，认为由于经济的动态无效性，公共债务(泡沫)是可以存在的，且公共债务的存在虽然会在当期实现帕累托改进，但对未来经济增长不利。Grossman和Yanagawa[5]研究了一种生产性储蓄和非生产性储蓄互动的经济。在该互动的经济下，经济增长内生决定于劳动生产率的提升；当经济动态无效时，资产泡沫会产生，且泡沫对经济增长有负向作用以及会降低泡沫之后出生的所有人的福利。King和Ferguson[6]研究了一个完全竞争的边做边学的经济。由于这种经济的外部性，经济体会处于动态无效状态，也为资产泡沫产生创造了条件，因而不利于经济增长。Wang Shengquan等[7]构建了银行持有资产泡沫的局部均衡模型，并实证检验发现资产泡沫发生通过恶化银行业稳定对经济增长产生不利影响。陈彦斌和刘哲希[8]构建了一个含有市场预期内生变化的DSGE 模型，认为资产泡沫会挤出对实体经济的投资，导致经济“脱实向虚”。

认为泡沫对经济增长有利的有以下代表性文献。Farhi和Tirole[9]将企业融资约束引入动态经济，认为经济即使处于动态下效泡沫也可能存在，且泡沫有放松融资约束的作用，因此可以促进经济增长。Martin和Ventura[10]观察到资产泡沫与经济波动的同步性，在Tirole[3]的基础上引入金融摩擦和资产泡沫的随机生成和破灭，表明资产泡沫与经济增长有正相关关系。Kunieda和Shibata[11]在一个无限生存的模型中证明了资产泡沫的可存在性，并且发现在不完美的金融市场上资产泡沫有助于异质性产率的投资者获取更多的信贷资金，因此有益于经济增长。Hirano和Yanagawa[12]在一个内生经济增长的模型中引入金融摩擦和异质性个体，证明当抵押贷款率很高及很低时资产泡沫不能存在，只有抵押贷款率介于中间时才会存在，且进一步证明当抵押贷款率相对较低时泡沫可以促进经济增长，但当抵押贷款了相对较高时不利于经济增长。

进一步，技术创新与资产泡沫两者间存在双向互动关系[12]。首先，技术创新会影响到资产泡沫产生的条件。Scheinkman[13]认为由于技术创新是促进经济增长的重要因素，经济增速上升会导致经济动态无效的概率上升，因此会增加泡沫存在的概率，相反泡沫会对由于技术创新带来的投融资产生影响。Shiller[14]和Lansing[15]认为技术创新发生后，投资者会对技术的真实进展情况做出过度反应，因此导致投机性泡沫。Comin等[16]、Kung和Schmid[17]也认为技术创新及其扩散是产出和资产价格变动的源泉。

其次，泡沫会对技术创新产生影响。Miao Jianjun和Wang Pengfei[18]提出一个信贷驱动的股票泡沫理论，认为股票泡沫可以使资源配置更有效，有助于全要素生产率的提升。Takao[19]在一个内生经济增长的框架下研究认为，资产泡沫会对市场结构产生影响；资产泡沫会利于大企业的产生，因此有增加研发支出的激励，从而利于经济增长。

综上，现有文献已从多个渠道研究了资产泡沫对经济增长产生的影响，但鲜有基于技术创新渠道的研究。此外，现有文献以理论研究为主，所得结论缺乏实证分析的支持。本文试图从以上两个角度弥补现有文献的不足。

本文所构建的理论模型提供了不同于现有文献的资产泡沫作用于经济增长的机制。在Aghion[20]的熊彼特经济增长模型基础上，引入融资约束。于此同时，本文使用2000-2016年我国的月度数据，结合使用新近发展的基于遗忘因子估计的时变参数和时变波动率的向量自回归(FF-TVP-SV-VAR)模型[21]和门限向量自回归(TVAR)模型对于资产泡沫发生、技术创新与经济增长之间的关系进行研究，实证分析的结论与理论分析的结论一致。

本文与现有文献相比，有以下几点贡献：第一，研究视角的创新，与现有文献强调泡沫对资源的再分配作用不同，本文借住熊彼特的创新性破坏增长理论，强调了研发部门在资产泡沫作用于经济增长中的重要作用。因此，本文是对泡沫的经济增长效应研究的有益拓展。第二，研究方法的创新。本文使用了新近发展的时变实证模型，能够捕捉经济机制的变动，从而弥补了该领域实证研究的不足。

本文的结构安排如下：第2部分刻画了我国经济的两个典型事实，第3部分构建了理论模型，第4部分是实证分析，最后一部分总结全文并提出政策建议。

3 中国经济的典型事实

本文理论模型的构建是建立在这两个典型事实的基础上：资产价格与技术创新存在较强的正相关关系；中国企业面临的融资约束问题较为突出。

2.1 资产价格与技术创新正相关

如前所述，资产价格波动与技术创新水平两者存在密切的关系。本文以上证综指和国内外专利受理量分别表示我国资产价格和技术创新水平，如图1所示，样本期内上证综指表现出较强的波动性，如2007-2009年和2014-2015年的大涨大跌，同样国内外专利受理量表现出明显的增长趋势和波动性。通过计算可得两者的相关系数为0.549，表明两者存在较强的正相关关系。

数据来源：国内外专利受理量数据来源于国家知识产权局发布的历年专利统计年报；上证综指来源于中经网统计数据库，经X2季节调整并取对数。

数据来源：国内外专利受理量数据来源于国家知识产权局发布的历年专利统计年报；上证综指来源于中经网统计数据库，经X2季节调整并取对数。图1 上证综指收盘价和国内外专利受理量的变动情况

长期来看，上证综指和国内外专利受理量均表现了增长趋势，也即伴随着资产价格的增长，我国技术创新水平也在不断提升。短期来看，上证综指和国内外专利受理量的波动是同步的，当上证综指处于上升期时，专利受理量也会经济偏离长期趋势的上涨，反之，则会出现专利受理量低于长期的趋势的情况。

对于资产价格和技术创新的正向关系的直观解释是，当资产价格处于上升通道，企业面临的抵押约束会得以放松，企业将更加便利为技术研发融资，从而专利数量也会增加，反之当资产价格处于下降通道，企业的抵押约束收紧，用于研发的资金相应减少，导致专利数量随之减少。

2.2 中国企业面临较严重的融资约束

参考陈彦斌和刘哲希[8]的做法，本文使用微观调查和宏观数据测算两种方式来反应我国企业面临的融资约束情况。

微观调查方面，本文采用中国人民银行企业家调查统计的资金周转指数，反映企业家对本企业本季资金周转情况判断的扩散指数。如图2所示，微观调查显示，从2010年开始，我国企业融资约束的难度进入波动中收紧的趋势。

图2 我国企业融资约束的变动情况

宏观数据方面，根据王国静和田国强[33]的方法，用国内贷款在全社会固定资产投资到位资金中的比重作为全社会企业面临融资约束程度的测度。该指标越大，表明固定资产到位资金中更多的来源于国内贷款，说明企业面临的融资约束越宽松。如图2所示，整体来看，国内贷款占固定资产投资到位资金的比重处于波动中下降趋势，即我国企业面临的融资约束处于收紧态势，企业融资越来越难。综上，无论是从微观调查还是宏观数据测算，均表明我国企业面临的融资约束程度较高，且处于不断收紧的态势。

4 理论模型

在Aghion[20]基础上，本文构建了一个简单的含有融资约束的熊彼特增长模型。考虑一个封闭的经济体，只存在一种最终产品，被称为一般性商品。该商品既可用于消费，也是中间品和研发部门的投入，且该商品在完全竞争的企业生产。假定工人生存在一个两周期的世代交叠模式中，且风险中性并最优化老年时期的预期消费。年轻时，他们在一般性商品生产部门工作，在完全竞争的劳动力市场获取工资。经济增长源于中间品生产部门产率的提升。在第二期期初，ε比例的工人有机会成为中间品部门的创新企业家，一旦创新成功，新型中间品就会被创造出来。这些创新企业家通过其自己的工资以及贷款来为创新活动融资。成功的企业家会支付贷款利息，第二期期末消费并且死去。总人口标准化为1。

3.1 一般性商品部门

一般性商品通过以下技术进行生产：

(1)

其中，α∈(0,1)，t表示时间，Lt表示劳动力投入，xt(i)是最新一代的中间投入品，At(i)是与之对应的生产率。出于简化，将劳动力正规化Lt=1，并将一般性商品作为计价物，可得中间投入品的价格等于其边际产出：

pt(i)=αAt(i)1-αxt(i)α-1

(2)

3.2 中间品部门

对每个中间品部门i，每期会有一个创新者出生。在t-1期出生的创新者会在第t期从事中间品的研发工作。令μt(i)为创新者研发成功的概率，因此中间品部门的生产率动态可表示为如下：

(3)

At=μtγAt-1+(1-μt)At-1

(4)

数据来源：资金周转指数来源于中国人民银行；固定资产投资资金各项数据来源于国家统计局，经X12季节调整。

因此，技术创新率为：

(5)

中间品生产的唯一投入品是一般性商品，且采用线性生产技术，成功的创新者i可以将一单位的一般性商品转化成一单位最新类型的中间品i。因此，可得成功创新者的利润为：

πt(i)=πAt(i)

(6)

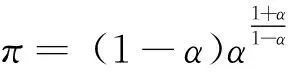
Gt=φAt

(7)

3.3 研发部门

创新成功的概率采用如下形式：

(8)

(9)

为进行创新活动，创新者需要为研发支出进行融资，贷款额为：Dt=Nt-ωt-1。由于道德风险的存在[8]，创新者的贷款上限为其预期收益的一定比例。即研发支出满足如下不等式：

(10)

其中，q<1为信贷乘数。由制度环境决定，该值越大表明融资约束越弱。当该约束成立时，该约束决定了最大的研发支出额。创新者通过选择研发支出Nt或创新概率μt以最大化其预期利润：

(11)

满足式(10)的约束，Rt表示利率。进一步可分为融资约束成立和融资约束不成立两种情况进行分析。首先，当融资约束不成立时，创新者最大化(11)式，可得无融资约束下创新成功的概率为：

(12)

结合式(9)，可得无融资约束下的研发支出为：

(13)

(14)

结合式(8)和(14)，可得受约束下的创新成功概率为：

(15)

3.4 资本市场

时间t时，贷款的供给量为非创新人群的工资额之和，贷款的预期回报是μtNt，机会成本即为储藏回报1。因此可得资金的总供给曲线为：

(16)

资金的总需求曲线为：

(17)

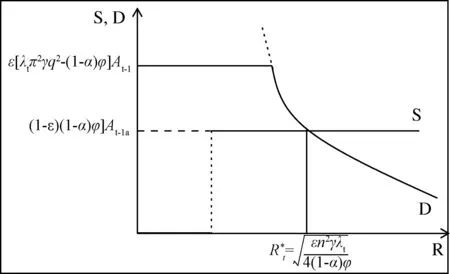
图3 无融资约束下的资本市场均衡

(18)

结合(6)、(12)、(18)，可得无约束的经济增长率为：

(19)

图4 受融资约束下的资本市场均衡

(20)

综上可见，存在两种方式应对融资约束下资本供给过度问题，即降低供给曲线和提高需求曲线。引入泡沫资产是降低资本供给曲线的方式之一，而研发部门的生产率冲击则是提高资本需求曲线的方式之一。

3.5 泡沫

很明显，无融资约束下，不存在过度的资本供给，因此理性资产泡沫是不可能存在的。然而，在有融资约束下，存在资本过度供给情况，理性资产泡沫的存在利于经济增长。考虑一种情形，在约束经济下，存在一种泡沫资产，该泡沫资产将δ比例的储蓄从年轻人转移到创新者，因此资本供给曲线(非零部分)将下降Bt=δ(1-ε)(1-α)φAt-1，假设泡沫资本在创新者间均等分配，则泡沫下每个创新者的研发投入为

3.6 生产率冲击

假设存在对研发部门的外生的生产率冲击，λt的上升会带来两种效应。一方面，由式(17)可知，资本需求曲线向下倾斜的部分会向外移动；另外，由式(8)可知，创新成功的概率将会提升，结合式(10)，预期收益增加，抵押品价值增加，起到了放松融资约束的效果，资金需求曲线的水平部分会上移。

3.7 理论模型的结论

从3.5和3.6的分析可以看出，正向的生产率冲击会增加创新成功的概率，会对经济增长产生推动作用。但是如果经济体面临较严重的融资约束，其经济增长很大程度上依赖于泡沫驱动。此时，正向的生产率冲击则会通过增加资本需求以减少资本供求的差距，从而限制了资产泡沫的产生，对经济增长产生负向作用。同样，当负向的生产率冲击发生，为泡沫资产的产生创造了条件，因此可能促进了经济增长。我们的分析类似于熊彼特的创新性破坏增长理论[22]。

4 实证分析

4.1 FF-TVP-SV-VAR模型和TAR模型

理论分析表明，资产价格泡沫通过技术创新对经济增长产生影响，但该机制发挥作用的前提是企业面临较强的融资约束，实证分析将对该结论进行检验。为达到此研究的目的，本文采取以下的实证策略。首先，使用Koop和Korobilis[21]提出的基于遗忘因子进行估计的TVP-SV-VAR模型。该模型的优点在于，可以刻画资产泡沫经济增长效应的时变性。该时变性的理论基础是企业面临融资约束的变化。与Primiceri[23]提出的MCMC估计方法不同，基于遗忘因子的估计方法能显著提升估计速度，尤其在模型维度较高时优势明显。其次，为进一步明确企业融资约束的门限值，即融资约束多大时资产泡沫促进经济增长的科技创新渠道才能发挥作用，本文使用TVAR模型对门限值进行估计。

TVP-SV-VAR模型可表示为：

Yt=Ztβt+εt

βt+1=βt+ut

(21)

βt-1|Yt-1～N(βt-1|t-1,Vt-1|t-1)

βt|Yt-1～N(βt|t-1,Vt|t-1)

(22)

其中，Vt|t-1=Vt-1|t-1+Qt，此处是Qt进入Kalman滤波的唯一地方。但如果将Vt|t-1表示成：

(23)

式(23)就没有必要对Qt进行模拟。此时，0<λ≤1被称为遗忘因子，可见当λ=1时，模型变为常系数模型。第j期的观测值在βt的滤波估计中的权重为λj。本文基准估计中，参考Raftery等[25]的设定，令λ=0.99。与以往基于后验模拟算法估计Σt不同，Koop和Korobilis[21]使用了几何加权移动平均过程来刻画波动率的变动，即：

(24)

TVAR模型可表示为：

(25)

其中，Wt为门限变量，既可以是Yt中的某个变量也可是外生的其它变量，τ为待估的门限值，I(·)为示性函数，括号内为真则取1，否则取0。参考石建勋等[27]，该模型的估计一般采用两步估计法：首先，给定τ的一个取值，利用线性回归法对(25)进行估计，得到残差平方和(SSR)，此时残差平方和为τ的函数；其次，将函数 SSR(τ)关于τ最小化，即可得到τ的取值。另外，可将(24)延伸至包含多个门限值的模型。

4.2 变量选取及数据

本文实证分析中应包括资产价格泡沫、技术创新、经济增长和融资约束四个变量。本文使用上证综指的波动率(sv)作为资产价格泡沫的代理变量。具体计算是，基于日度上证综指收盘价计算日历月度内的标准差，作为该月度上证综指的波动率。以波动率作为资产价格泡沫的代理变量是因为，现有研究表明，波动越大说明股权资产价格变动越剧烈，股市泡沫发生的概率越大[28]。除此之外，Iraola和Santos[29]认为基本面信息(如分红、利润等)波动往往较小，因此股价高波动无法由基本面信息的变动所解释。Lansing[15]认为投机行为会放大经济和金融变量的波动性。这些证据可以支持使用股价波动作为泡沫代理变量的合理性。图5绘制了上证综指波动率变动情况，可见存在两个明显的高波动区间，即2007-2009年和2015-2016年，前者是金融危机时期，后者则是我国股市“2015年的疯狂”时期。显然，这两个时期股市泡沫化较为严重。因此，本文认为资产价格波动率是资产价格泡沫的良好代理变量。

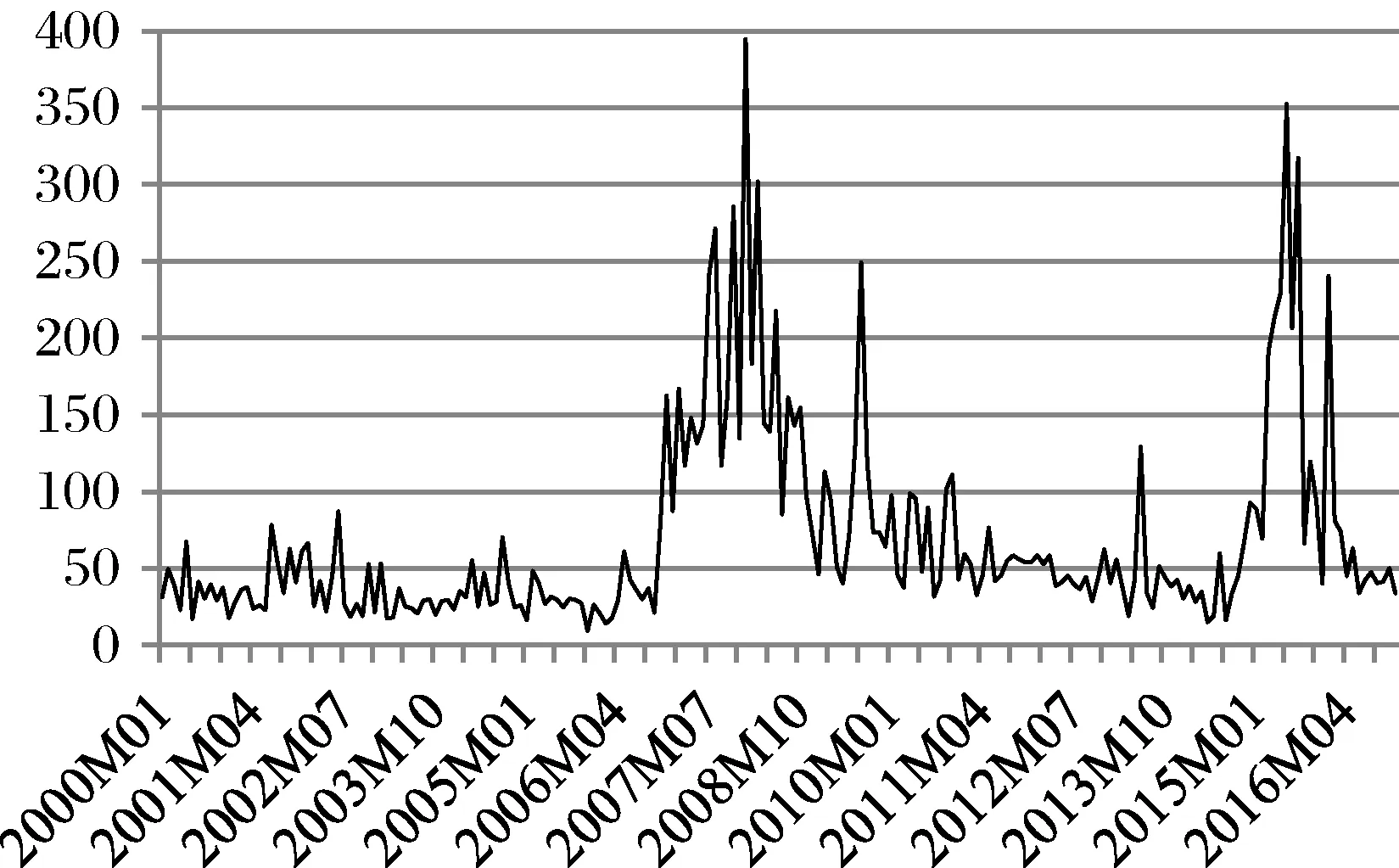
图5 上证综指波动率变动情况

参考Dosi等[30]、李苗苗等[31]和周煊等[32]，本文使用专利数据作为技术创新水平的代理变量，考虑到数据的可得性，具体使用国内外专利受理量(ti)。与研发数据相比，专利数据更能反映企业的技术创新水平，因为技术创新是资源投入和使用效率的最终体现，代表创新产出的专利数量能更好地体现企业的创新能力。本文使用工业增加值的实际环比增长率(og)最为产出增长率的代理变量。参考王国静和田国强[33]，本文使用国内贷款在全社会固定资产投资到位资金中的比重(fc)作为全社会企业面临融资约束程度的测度。数据来源方面，上证综指日度收盘价数据来源于WIND数据库，国内外专利受理量数据来源于国家专利局发布的历年专利统计年报，工业增加值的实际环比增长率数据和社会固定资产投资到位资金各相关数据来源于中经网统计数据库。数据长度为2000年1月至2016年12月，共计204个观测值。

4.3 数据检验与描述

在实证研究前需要对使用的数据进行处理与统计检验。首先，对四个变量进行X12的季节性调整，以消除季节性变动趋势对实证结果的干扰，另外对科技创新变量通过HP滤波去除趋势项成分。其次，在VAR框架下做实证研究，需要保证所用数据的平稳性，以避免“伪回归”问题的出现。本文使用ADF 统计量对各变量进行单位根检验，结果如表1 所示。股价波动率、科技创新、融资约束三个变量分别在1%、1%和5%的置信水平下拒绝存在单位根的原假设，即股价波动率、科技创新、融资约束均平稳，而产出增速不能拒绝单位根存在的原假设，经一阶差分后在1%显著水平下平稳。因此，在模型估计时本文使用的是股价波动率、科技创新、融资约束的水平值和产出增速的一阶差分值(改变变量顺序，实证结果不变)。

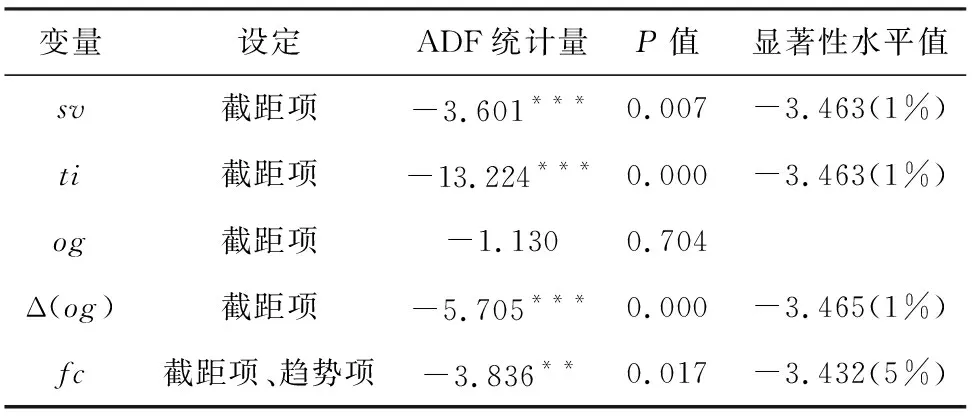
表1 各变量单位根检验结果

表2报告了各变量的统计描述。可见，股价波动明显，标准差达65.771，最小值与最大值相差约43倍，且分布呈现出右偏且高尖峰特征。科技创新波动程度最小，标准差为0.150，呈现出左偏且高尖峰的分布特征。产出增速的变动和融资约束的波动类似，标准差分别为4.283和4.584，前者呈现左偏且高尖峰的分布特征，后者则呈现出轻微左偏且低尖峰的分布特征。

表2 各变量描述性统计

进一步，可通过如表3所示的相关系数矩阵初步确定各变量之间的相关性。首先，股价波动率与技术创新的相关系数为-0.004，这与Hirano和Yanagawa[12]的观点一致，即技术创新与资产泡沫两者间存在双向互动关系。其次，融资约束与股价波动率的相关系数为-0.249，该关系的可能解释是，资产泡沫源于金融市场的不完美性[34]，融资约束放松(fc值上升)自然会降低泡沫发生的概率，即资产价格波动率下降。再次，融资约束与技术创新的相关系数为-0.016，表明当企业面临的融资约束越高(fc值越小)时，专利受理量越多，即科技创新水平越高，这符合前文理论分析的结果。

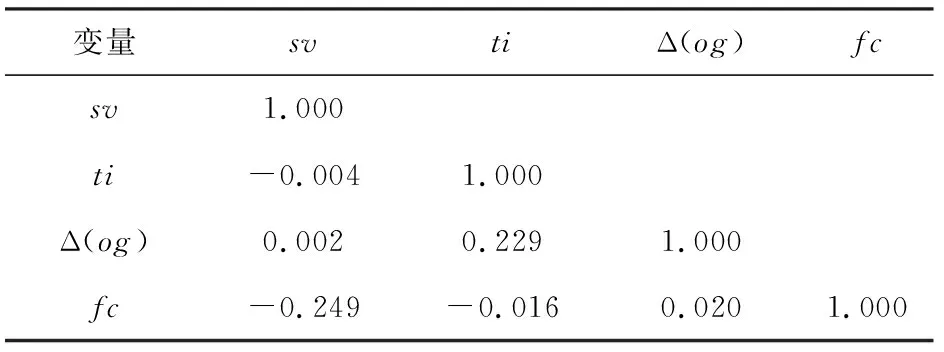
表3 各变量相关系数矩阵

需要指出的是，全样本来看，股价波动与产出增速的一阶差分相关系数为0.002。但若按照融资约束大小分段来看，2000M1-2008M12期间，平均融资约束为22.403，此时相关系数为-0.060，表明资产价格波动会对产出增速变动产生负向影响。2009M1-2016M12期间，平均融资约束为14.605，此时相关系数为0.057，表明资产价格波动对产生增速变动产生正向影响。造成这样结果的可能原因可由前文的理论分析解释，即只有当企业面临较为严重的融资约束时资产泡沫才能通过促进技术创新的渠道对产出增速产生正向效应。

4.4 实证结果与分析

首先，使用FF-TVP-SV-VAR模型分析资产泡沫冲击的经济增长效应和技术创新效应。根据SIC，确定模型的最优滞后阶数为2。

图6绘制了当发生正向的股票价格波动率冲击，即资产价格泡沫发生概率上升，产出增速变动的脉冲响应。由图6-A可见，产出增速变动对股价波动率冲击的脉冲响应表现出时变特征，不同时间点上脉冲响应的程度、持久性甚至方向都表现出异质性。根据脉冲响应的表现特征可将股价波动率冲击对产出增速变动的影响分为三个阶段，第一个阶段(2000-2007年)，该阶段股价泡沫的发生对经济增长产生了负向影响，如图6-B中2002年4月的脉冲响应，一个标准差的股价波动率冲击会导致下一期产出增速变动偏离均衡状态-0.04，产出增速的变动在约八个月后回复至均衡状态；第二阶段(2008-2014年)，该阶段股价泡沫的发生对经济增长产生的作用可能为正也可能为负，如图6-B中的2009年6月和2010年6月的脉冲响应，前者表明股价波动率冲击利于产出增速的变动，而后者则产生了轻微的负向影响；第三阶段(2015-2016年)，该阶段资产泡沫发生对经济增长产生了促进作用，如图6-B中2016年2月的脉冲响应，股价波动率冲击导致产出增速变动偏离均衡状态约0.032，该影响在第八期后逐渐消失。

图6 产出增速变动对股票价格波动率冲击的脉冲响应

图7绘制了股价波动率冲击发生对技术创新造成的影响。如图所示，技术创新对股价波动率冲击的脉冲响应基本为正，即资产泡沫的发生通过抵押约束放松渠道对放松了企业为技术创新的融资，因此泡沫发生利于技术创新，这与前文的理论分析一致。另外，可以看到，样本期内脉冲响应表现出明显的时变特征，基本的趋势是技术创新对股价波动率冲击的反应变得越来越强烈。如前文的分析，我国企业面临的融资约束程度在不断加深，而随着融资约束的收紧，资产泡沫的发生越能起到放松融资约束的作用，因此技术创新得了更多的实现，具体来看，在样本初期，企业面临的融资约束相对宽松，此时发生股价波动率冲击会导致技术创新偏离均衡状态约0.005，在第二期达到最大，在第八期逐渐消失，但在样本期末，企业面临的融资约束相对紧张，此时发生股价波动率冲击会导致技术创新偏离均衡状态约0.025，是前者的5倍。

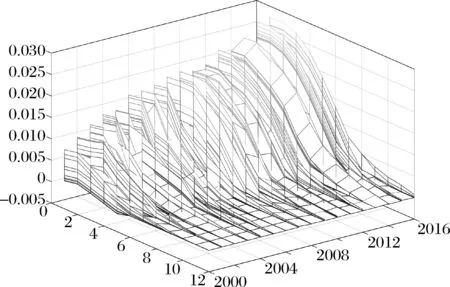
图7 技术创新对股票价格波动率冲击的脉冲响应

结合图6和图7可表明在资产价格泡沫影响经济增长的过程中“技术创新”渠道发挥着重要的作用。在样本初期，企业面临的融资约束相对宽松，此时发生资产泡沫对技术创新的正向作用较弱，资产泡沫通过其他渠道，如陈彦斌和刘哲希[14]提出的泡沫挤出投资渠道，对经济增长产生的负面影响超过了技术创新的正面效应，表现为图6所示的脉冲响应为负值。

在样本末期，企业面临的融资约束相对紧张，此时资产泡沫发生会对技术创新产生较强的正向促进作用，即企业融资约束的变化改变了资产泡沫发生与技术创新的关系，这与现有研究认为企业融资约束与创新绩效之间存在显著的倒U型关系的观点一致[34]。虽然资产泡沫可能通过其他渠道对经济增长产生负向作用，但资产泡沫的正向技术创新效应大过其他渠道的负向效应，因此表现出如图6所示的脉冲响应为正值。而介于两者之间时，资产泡沫的经济增长效应的正负取决于其他渠道和技术创新渠道对经济增长产生作用的相对大小，结果表现为图6所示的脉冲响应时负时正。

为进一步确定“资产泡沫通过技术创新对经济增长产生作用”该机制所依赖的融资约束的临界值，本文使用TVAR模型对此进行识别。根据SIC确定最优的滞后阶数为2。本文以融资约束为门限变量，分别进行了一个门限值和两个门限值的识别，识别过程如图8所示。在一个门限值的模型中可以看到(图8-A)，当融资约束>12.697时，此时融资约束相对宽松，资产泡沫发生并不能对企业技术创新产生促进作用。

相反，当融资约束≤12.697时，此时融资约束相对紧张，资产泡沫发生起到了放松企业为技术创新融资的约束。在两个门限值的模型中(图8-B)，识别出的两个融资约束的门限值分别为12.697和18.561，与一个门限的模型不同的是此时识别出了一个模糊的区域，即当融资约束介于两个门限值之间时，资产泡沫发生对技术创新的影响是不明确的。总之，TVAR模型的使用进一步检验了本文的理论结论，通过门限值的识别也是对研究结论进一步丰富。根据上文两个门限值的设定，将样本划分为三个子区间，但由于子区间在时间上的非连续性，因此无法对变量之间进行Granger因果检验，但可通过观测TVAR模型中各变量系数的变化来确定融资约束的高低对“资产泡沫通过技术创新对经济增长产生作用”机制产生的非对称影响。表4分区间汇报了TVAR模型的回归结果。表明资产价格泡沫的产生利于科技创新成果的增加，同样对产出增速变动的影响系数为1.875，表明此时发生资产泡沫是对经济增长有利的。在区间3上，此时企业面临较为宽松的融资约束，股价波动率的滞后一期对科技创新和产出增速变动的影响系数分别-0.544和-0.102，表明此时发生资产泡沫不利于企业科技创新，会对经济增长产生负向作用。在区间2上，此时企业面临中等的融资约束，在本样本内，资产泡沫发生会对企业科技创新和经济增长产生轻微的负面影响。因此，该回归结果与前文的理论结论一致。

图8 融资约束门限值的识别过程

4.5 进一步检验

进一步，我们使用转移概率时变的马尔科夫区制转移向量自回归(TVTP-MS-VAR)模型[35]检验资产泡沫发生、技术创新与经济增长之间存在的区制转移关系。如TVAR模型的结果表面，三者关系至少存在三个区制，即高融资约束、中等融资约束和低融资约束。TVTP-MS-VAR模型的回归参数估计结果与表4基本一致，在此不再赘述。图9绘制了每个时间点三者关系所处的区制概率。如图9可见，在样本前期(2007年之前)，三者关系大多数情况下处于区制1，对应于前文中的低融资约束期间；样本中期(2008-2012年之间)，三者关系所处区制变动较大，意味着三者关系不明确，对应于前文中的中等融资约束期间；样本后期(2013年之后)，三者关系大多数情况下处于区制3，对应于前文中的高融资约束期间。因此，使用MS-VAR模型检验出资产泡沫发生、技术创新与经济增长三者关系存在区制转移特征，证明了前文实证研究的稳健性。

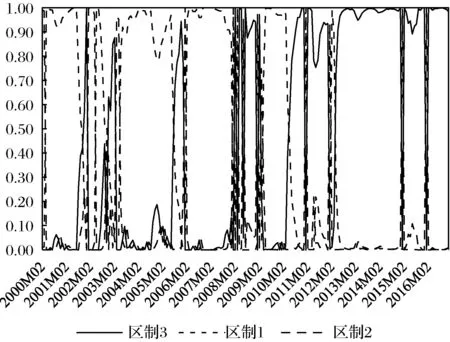
图9 区制概率变动情况

表4 TVAR模型的回归结果

5 结语

当前，我国经济正在发生着增长动力的转换。在此背景下，本文从理论和实证两方面研究了资产价格泡沫发生通过技术创新渠道对经济增长产生影响。理论方面，本文基于Aghion[12]模型构建了符合我国实际的熊彼特增长理论的分析框架。该框架融合了我国经济的两个典型事实，即技术创新与资产价格正相关、我国企业面临较为严重的融资约束。企业家为研发进行融资。由于融资约束的存在，资本市场会出现资金供给大于需求的情况，此时企业家可通过生产泡沫资产的形式获取资金，最终达到资本市场的均衡。显然，企业家得到了研发所需资金，增加研发投入，研发成功的概率上升。因此，有泡沫时的经济增速会高于无泡沫时的经济增速，即资产泡沫可通过“技术创新”效应促进经济增长。

基于以上的理论分析，本文使用了新近发展的基于遗忘因子估计的TVP-SV-VAR模型和TVAR模型，并结合我国2000-2016年月度数据开展实证研究。首先，实证分析的结论与理论研究一致，即资产价格泡沫可促进企业技术创新，进而利于经济稳增长。其次，实证研究表明，资产泡沫的技术创新效应的强弱取决于企业面临的融资约束程度，表现出时变特征，企业面临融资约束越紧，资产泡沫的技术创新效应越强。再次，借住TVAR模型，本文识别了样本期内我国融资约束的两个门限值，即12.697和18.561，低于12.697时，资产泡沫可通过技术创新效应促进经济增长，高于18.561时，资产泡沫的技术创新效应较弱，资产泡沫通过其他渠道对经济增长产生负向作用。进一步，使用TVTP-MS-VAR证明了以上研究结论的稳健性。

本文研究有丰富的政策含义。首先，资产泡沫可以发挥促进经济增长的作用，尤其在当前我国企业面临较为严重的融资约束的情况下，政府部门应监控企业融资约束的变化，积极引导资金流入研发部门，实现“创新驱动”发展战略。其次，资产泡沫在一定条件下虽然能促进经济增长，但资产价格不能过度膨胀，严重的泡沫将触发系统性风险，不利于稳增长。因此，政府部门应及时对过度泡沫化的资产价格进行有效调控。