基于黎曼流形的MIMO 雷达目标检测方法

周美含, 姜 宏, 孙 帅

(吉林大学 通信工程学院, 长春130012)

0 引 言

多输入多输出(MIMO: Multiple-input Multiple-output) 雷达是2004 年提出的一种新兴雷达系统[1],它能将MIMO 通信与雷达领域相结合, 而目标检测作为MIMO 雷达系统中的重要领域[2-4], 引起了学者们的广泛关注。 目前, MIMO 雷达的目标检测方法包含广义似然比检测[5]、 奈曼皮尔逊检测[6]、 压缩感知检测[7]和恒虚警检测[8]等, 这些方法虽然可以提高目标检测性能, 但当存在信噪比较低、 快拍数较少甚至单快拍的情况时, 检测结果将存在较大误差。

近年来, 考虑拓普利兹-厄米特正定(THPD: Toeplitz Hermitian Positive Definite)矩阵会在信号空间中形成流形[9-11]现象, 将黎曼流形应用于各个领域已经成为学术界的一个研究热点, 如水声通信[12]、物理学[13]、 神经网络[14]、 图像处理[15]和通信编码[16]等领域。 文献[17] 利用黎曼流形理论设计了一种信号分类方法; 文献[18]以黎曼流形为数学理论, 研究了对称正定矩阵的黎曼距离。 文献[19]进一步扩充了黎曼距离及黎曼均值的计算方法。 当快拍数较小时, 样本协方差矩阵则不能代替统计协方差矩阵,假设接收信号和噪声的协方差矩阵位于黎曼流形上的两点, 则可利用流形上的最短距离即黎曼距离判断它们的相似性。 笔者在文献[19]的基础上, 提出一种基于黎曼流形和burg 递推法的单基地MIMO 雷达目标检测新方法, 即通过burg 递推法分别生成单快拍下接收信号和噪声的THPD 协方差矩阵, 并求解噪声THPD 协方差矩阵的黎曼均值, 将其与接收信号THPD 协方差矩阵间的黎曼距离作为检测统计量, 并根据虚警概率以及噪声的统计分布推导出判决阈值, 从而实现低信噪比和单快拍下的目标检测。

1 单基地MIMO 雷达信号模型

考虑一个收发阵元均为均匀线阵的单基地MIMO 雷达系统, 分别采用M 和N 个发射阵元和接收阵元同时发射和接收信号。 假定有一个远场窄带目标, 其收发方向角均为θ, 则接收信号矩阵可表示为

其中ar( θ) = [1, e-j2πsin(θ)d/λ,…, e-j2πsin(θ)(N-1)d/λ]T表 示 接 收 导 向 矢 量, at( θ) = [ 1, e-j2πsin(θ)d/λ, …,e-j2πsin(θ)(M-1)d/λ]T表示发射导向矢量, d 和 λ 分别表示阵元间距离和信号波长, β 为单快拍下的目标散射系数, S 为M 个发射波形组成的归一化正交矩阵, 且SSH=IM, Z 是高斯噪声矩阵。 对接收信号矩阵X 进行匹配滤波和矢量化处理后, 可得到单快拍下的观测信号矢量

其中a =at(θ)⊗ar(θ)为MN×1 维发射-接收联合导向矢量, ⊗为Kronecker 积; z 为处理后的MN×1 维的噪声矢量。

2 THPD 协方差矩阵

在计算协方差矩阵的过程中, 传统方法通常用样本协方差矩阵代替统计协方差矩阵, 但当快拍数较小甚至为单快拍时, 这种方法将不再适用, 笔者采用burg 递推法对观测信号矢量y 的统计协方差矩阵进行估计。 首先, 将y 表示为

则y 的统计协方差矩阵R 为一个THPD 矩阵, 可表示为

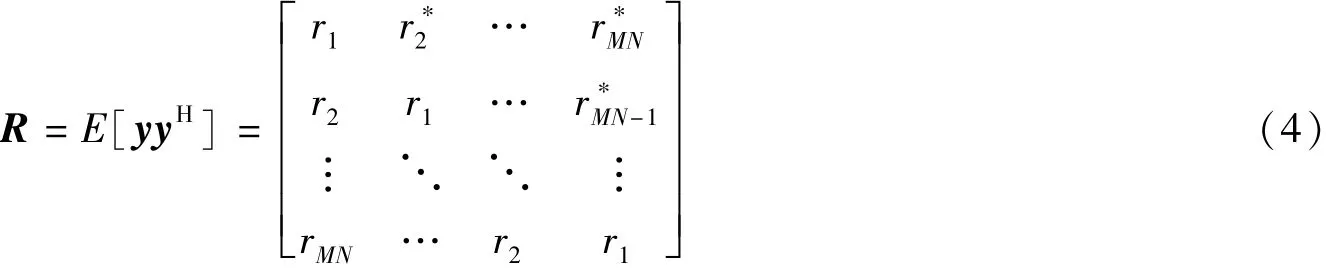
其中rm=E[y1y*m], m=1,…,MN。

对R 的每个元素进行burg 计算, 设前、 后向预测误差以及预测误差功率的初始值分别为

则对阶次m=1,…,MN, 前向误差fm和后向误差bm的递推关系分别为

其中km为反射系数, 其计算方法为[20]

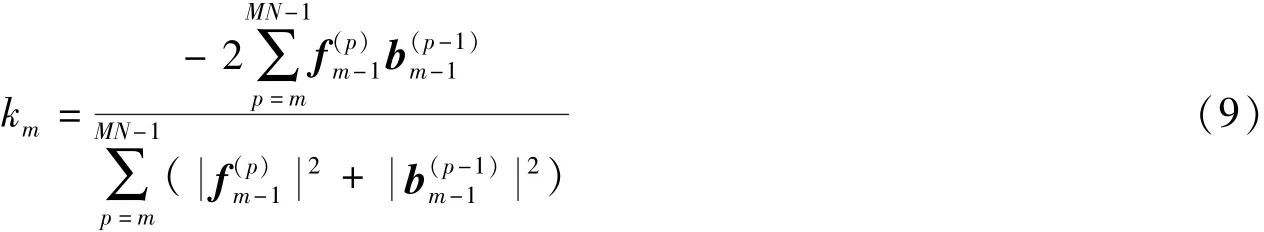
其中f(p)m-1、b(p)m-1分别表示fm、bm从第p 行开始截取的子矢量, 根据反射系数及Levinson-Durbin 公式, 得burg 递推法模型系数为

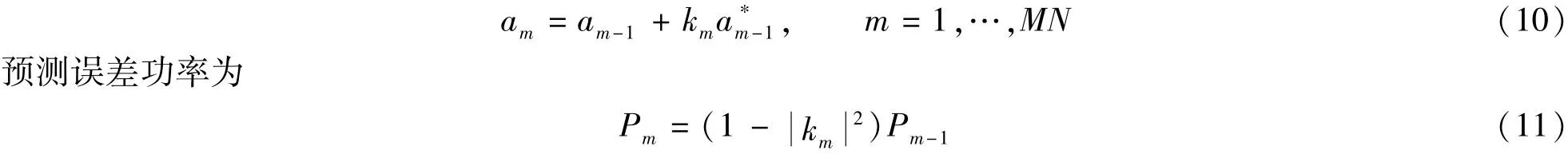
最后, 利用如下burg 递推方法估计R 中的每个元素

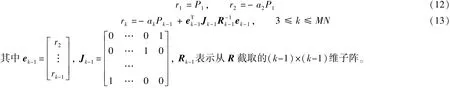
3 基于黎曼流形的目标检测方法

3.1 黎曼距离

笔者方法的目标是增加接收信号与噪声间的差异性。 由于THPD 矩阵会在信号空间中形成黎曼流形, 分别使用如下两种黎曼距离[19]进行度量

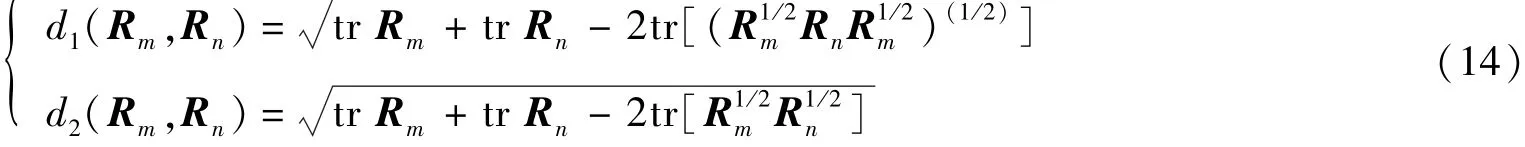
其中Rm和Rn是黎曼流形上存在的任意两个THPD 协方差矩阵。

3.2 黎曼均值

实际环境中得不到确切的噪声均值, 所以需要计算多次观测噪声THPD 协方差矩阵的黎曼均值, 作为后续目标检测的噪声均值。 假设单快拍下的观测噪声矢量为

由d1推导黎曼均值MR1: 收集L 个噪声矢量的THPD 协方差矩阵, 用Rlz(l=1,…,L)表示, 则L 个噪声THPD 协方差矩阵的算术平均矩阵为

根据黎曼流形的等距映射, 定义函数

对(Rlz)1/2M1进行奇异值分解, 并将左、 右奇异值矩阵Ul、Vl与噪声矩阵相乘, 得

其中d1(M′,M)表示M′与M之间的黎曼距离。 设局部阈值为ε, 若h＞ε, 用M″代替M继续迭代; 若h＜ε, 迭代中止, 此时得出黎曼均值为MR1=M′。

由d2推导黎曼均值

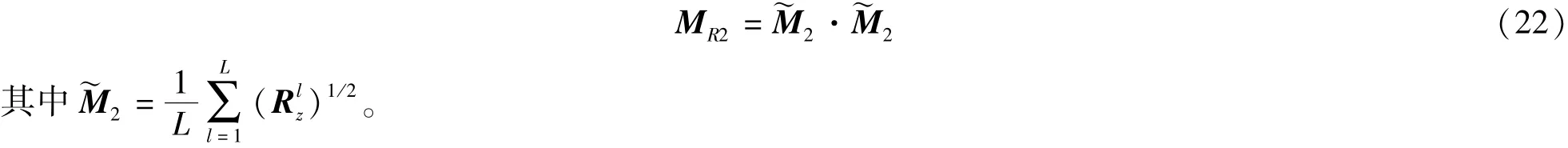
3.3 目标检测的二元假设检验模型

将y的THPD 协方差矩阵R与噪声的黎曼均值MR之间的黎曼距离作为检测统计量T, 即

为得到判决阈值, 分别用H0和H1表示目标存在和不存在的情况, 根据噪声的黎曼均值得出统计分布, 并定义虚警概率Pfa与阈值rα的关系为

4 仿真结果及分析

对笔者所提算法的有效性进行验证。 考虑高斯白噪声背景, 发射和接收阵元数分别为M= 8,N= 3,收发方向角为θ=20°, 进行1 000 次蒙特卡罗实验。

图1 和图2 分别为MR1和MR2两种黎曼均值情况下, 采用和不采用burg 处理方法的检测概率与信噪比(SNR: Signal-to-Noise Ratio,RSNR)关系曲线。 仿真中, 虚警概率为Pfa=0.1。 仿真结果表明, 在单快拍数时, 利用burg 递推法对协方差矩阵进行处理是可行的, 即预先经过burg 处理可有效提升目标的检测性能。

图1 MR1情况下采用和不采用burg 处理方法对比Fig.1 Comparison of methods with MR1 and without burg under

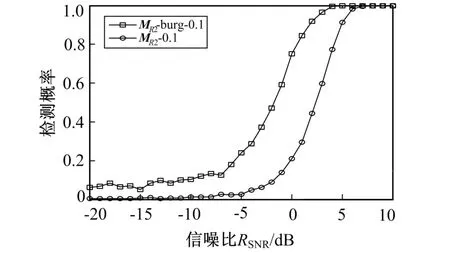
图2 MR2情况下采用和不采用burg 处理方法对比Fig.2 Comparison of methods with MR2 and without burg under

在验证了burg 递推法的合理性后, 将笔者提出的基于黎曼距离和黎曼均值MR1和MR2的两种检测方法与传统基于欧几里得距离和均值ME的检测方法进行了性能对比, 在采用和不采用burg 递推法的情况下, 分别得出Pfa=0.01 时检测概率与SNR 关系曲线, 如图3 所示, 其局部放大图如图4 所示。 其中MR1-burg、MR2-burg 和ME-burg 分别表示基于MR1,MR2和ME并结合burg 递推的目标检测方法。

图3 和图4 的仿真结果表明, 这6 种方法的检测概率都随信噪比的增加而增加。 其中,MR1-burg 方法的检测性能最优, 其次是MR2-burg 方法, 而ME方法最差。 尤其是在RSNR=0 时,MR1-burg 方法检测概率仍接近100%, 而此时ME方法的检测性能严重下降。 因此, 笔者所提出的基于黎曼流形和burg 递推的检测方法始终保持优越的检测性能, 且适合于低SNR 和单快拍环境。

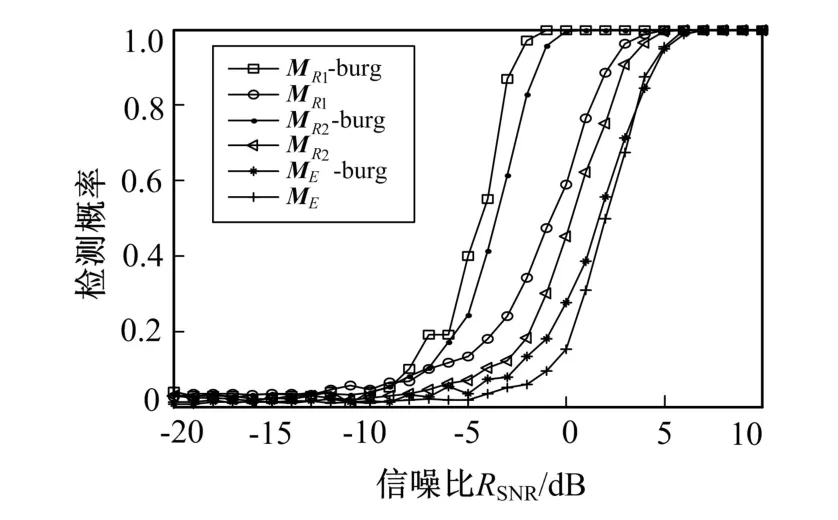
图3 Pfa =0.01 时不同方法的性能对比Fig.3 Performance of different methods when Pfa =0.01

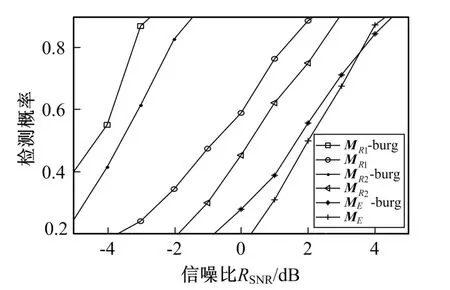
图4 对图3 的局部放大图Fig.4 Partially enlarged view of Fig.3

5 结 语

笔者提出了一种基于黎曼流形的单基地MIMO 雷达目标检测方法, 该方法通过burg 递推法分别生成单快拍下接收信号和噪声的THPD 协方差矩阵, 并充分利用THPD 矩阵在信号空间中形成的黎曼流形,基于黎曼均值和黎曼距离实现目标检测, 解决了低信噪比下目标检测性能较差的问题。 仿真结果表明,与传统利用欧几里得均值和距离进行检测的方法相比, 在低信噪比和单快拍的MIMO 雷达环境中, 笔者所提出的方法具有更好的目标检测性能。