近空间飞行器机翼动态可靠性分析

周泽宇, 王玉惠, 吴庆宪

(南京航空航天大学 自动化学院, 南京210006)

0 引 言

执行近空间高超声速飞行任务时, 随着飞行高度、 速度的增加以及飞行姿态的不断改变, 近空间飞行器与大气相互作用产生复杂气动力, 使作为主要受力面的机翼表面存在复杂的气动载荷分布。 除此之外, 高超流的激波干扰、 结构部件的受力变化以及复杂的气动热, 导致飞行器机翼更容易产生结构疲劳。因此, 为保证飞行器的结构可靠和飞行安全, 开展近空间飞行器机翼结构动态可靠性分析和寿命预测是十分必要的。

关于结构可靠性的研究, 主要包括静态和动态可靠性分析。 静态可靠性分析主要针对结构受力和材料强度为定值时的可靠度的计算, 文献[1-5]针对不同结构的可靠度计算取得了一定的成果; 而对动态可靠性的研究则考虑了结构受力或材料强度的变化[6-10]。 文献[6]给出了多种载荷作用下的可靠性预测模型, 但主要针对等幅载荷作用时的可靠性分析, 否则结果误差会偏大。 文献[7-8] 考虑了多次载荷作用下结构可靠性问题, 但未考虑结构强度由于振动等原因而造成的退化问题。 文献[9-10]研究了动载荷下的结构动态可靠性问题, 建立了结构动态可靠性预测模型, 并通过算例验证了模型符合工程实际。 在文献[6-10]的动态可靠性的研究基础上, 文献[11-12]开展了机翼强度的可靠性研究, 但进行寿命分析时, 未考虑到参数的随机性对分析结果的影响。 实际上, 由于近空间飞行环境恶劣、 飞行器飞行动态复杂及其材料特性误差和机械结构疲劳等因素, 使飞行过程中的机翼强度和载荷的作用次数都存在随机分散性。 因此, 为保证飞行安全, 需要探索新的适合近空间飞行器机翼的动态可靠性的研究方法。

综上分析, 笔者考虑随机载荷和强度变化, 基于近空间飞行器机翼动态模型和受力分析, 给出了机翼动态可靠性研究的一种新方法。 受文献[13]启发引入泊松随机过程表征载荷作用次数, 在机翼强度干涉理论的分析结构强度的基础上[14], 结合近空间飞行器飞行环境以及飞行状况, 提出截尾正态分布描述气动载荷的新方案, 对近空间飞行器的机翼强度可靠性进行了全面地分析, 建立了动态可靠性模型, 并分析了强度退化和飞行速度、 高度、 迎角对可靠性的影响, 给出了保证飞行器结构可靠性的基本要求,为今后的结构可靠性控制器设计提供重要参考。

1 机翼应力分析

由于近空间飞行器在高超声速飞行过程中受到复杂气动力的作用, 加上机翼本身结构复杂, 很难对其受力进行准确分析。 为此, 笔者将从分布力和表面受力入手, 分析某一截面的受力情况。 不失一般性, 视机翼为薄翼型。

近空间飞行器执行飞行任务时, 机翼的受力主要包括机翼重力Gw, 升力Lw和阻力Dw。Lw与Dw可表示为

其中1/2ρV2为动压, 用¯q表示,ρ为空气密度,V为空速,Sw为单个机翼参考面积,CL为机翼升力系数,CD为机翼阻力系数,CL和CD都是关于Ma(马赫数)、 迎角α和气动舵面的函数。 考虑升力、 阻力和重力引起的压强分别为: 平均翼面升力压强、 平均翼面阻力压强PDW=DW / SW以及平均翼面重力压强PGW=GW / SW。

为分析机翼的受力情况, 需研究某一截面上的受力分析[15]。 首先选取一目标截面Sd(见图1),Sd受到的弯曲力矩为由翼尖到此截面的各面对其的合力矩。设其中某一截面为Sx, 其受到的合力通过压强PLW、PDW、PGW在迎角α下计算求得, 则截面Sd绕机体x轴的弯曲力矩Mblx和绕机体z轴的弯曲力矩Mblz为

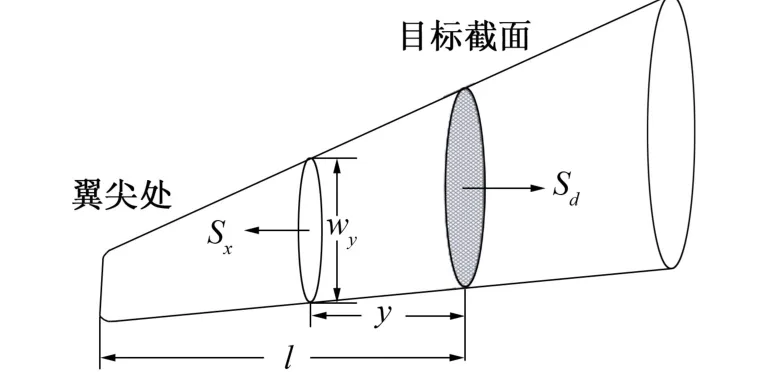
图1 计算截面弯矩的示意图Fig.1 Schematic diagram for calculating section bending moment

其中wy是Sx的截面宽度, l 是翼尖到Sd的距离, γ 为飞行器的航迹倾斜角。

1) 拉压应力。 基于结构力学, 绕两个机体轴目标截面的拉压应力可分别表示为

其中Ilx和Ilz分别是关于中性轴x 轴和z 轴的惯性矩。 认为机翼截面为椭圆形, 截面的宽度、 高度与翼尖的距离成正线性关系, 其任意截面的惯性矩可表示为

其中wl和hl分别是距离翼尖l 处截面的宽度和高度。

2) 剪切应力。 类似于计算弯曲力矩的思路, 目标截面Sd沿机体轴x 轴和z 轴的剪切力可表示为

则沿两个机体轴的剪切应力为

其中Sl是截面Sd的面积。

3) 相当应力。 基于应力叠加原理, 目标截面所受的拉压应力和剪切应力的合力为

其中相当应力σl即为目标截面受到的载荷应力。

2 近空间飞行器机翼可靠性建模

文献[14]模拟了高超声速飞行器在高超声速巡航飞行时机翼截面的损伤演化情况, 结果表明飞行器在翼根截面累积损伤最为严重。 因此, 结合文献[14]的结论, 笔者在应力分析的基础上, 着重计算翼根截面处的应力, 并进行可靠性分析。 为了分析不同飞行动态时机翼可靠性的动态变化, 需要考虑飞行器的气动动态。 根据NASA 报告[15], 给出气动系数表达式为

其中CL,α,CD,α分别为基本升力系数和基本阻力系数; δe,δα分别为左、 右升降副翼舵; CδeL,CδαL分别为左、右升降副翼舵引起的升力增量系数; CδeD,CδαD分别为左、 右升降副翼舵引起的阻力增量系数。

将式(16)、式(17)代入式(1)和式(2), 便可计算出不同飞行动态时机翼受到的升力Lw和阻力Dw。给定单个机翼参考面积Sw=167.36 m2, 以及平均气动弦长c=24.38 m, 考虑机翼为薄翼型可近似计算出单个机翼翼展为Sw/ c=6.864 64 m。 此外, 根据空气动力学基础[16], 其中在近空间(20 ～35 km)飞行时大气密度与高度的关系如图2 所示。

在给定飞行速度、 高度的情况下, 基于¯q =1 / 2ρV2则可计算出动压大小。

图2 近空间(20 ～35 km)的大气密度变化Fig.2 Variation of atmospheric density in near space (20 ～35 km)

再由式(5)、 式(6)、 式(13)得到近空间飞行器飞行时机翼翼根截面处所受到的拉压应力σbl; 同理,由式(11)、 式(12) 和式(14) 可计算机翼翼根的剪切应力τQl; 合力的相当应力σl由式(15)计算。 具体计算结果如表1 所示。

由表1 可知, 拉压应力σbl, 剪切应力τQl以及合力的相当应力σl变化趋势一致, 飞行指标的变化导致两种应力同时增大或减小, 此外, 两种应力对结构可靠性影响等效于σl对飞行器机翼的影响, 因此以下的可靠性理论着重分析合力的相当应力σl即可。对比表1 中的应力数据可知, 应力随着马赫数的增加而增加, 随着高度的增加而减小, 随着迎角的增加而增加。 与实际飞行试验结果[17]对比可知, 表1 的计算结果是合理的, 且对照数据, 这里考虑近空间飞行器在高超声速飞行过程中翼根受到的应力载荷服从参数为μs=110.34 Mpa,σs=46.27 Mpa 的截尾正态分布。

表1 近空间飞行器机翼翼根的应力Tab.1 Stress of wing root of near space vehicle

参考X-43A 以及X-51A 项目, 目前进行的实际飞行试验的高超声速飞行器机翼的主体承力结构所用材料多为Haynes 镍基合金, 并在机翼表面覆盖碳-碳、 碳化硅等热防护材料。 文献[18]给出了不同温度下Haynes230 合金的力学性能和Haynes230 合金蜂窝夹层板室温力学性能, 表明随着温度提高抗拉强度和名义屈服极限逐渐减小, 延伸率在逐步提升。 从文献[19]可知, 当温度高于800 ℃时, 力学性能会随着温度升高有明显下降趋势, 一般情况下, 认为该合金在800 ℃以内的力学性能较为稳定。 因此, 这里考虑翼根截面的温度在500 ℃左右[20]。 结合镍基合金强度特性计算得到, 在500 ℃左右, 材料的名义屈服强度服从参数为μδ=283.51 Mpa,σδ=12.51 Mpa 的截尾正态分布。

笔者用δ表示镍基合金强度, 令其累积分布函数为Fδ(δ), 概率密度函数为fδ(δ); 用S表示翼根截面处所受到的相当应力σl, 其累积分布函数为FS(S), 概率密度函数为fS(S)。 从上述分析可知δ和S均为正值, 且都服从均值方差不同的截尾正态分布, 其分布函数如下所示

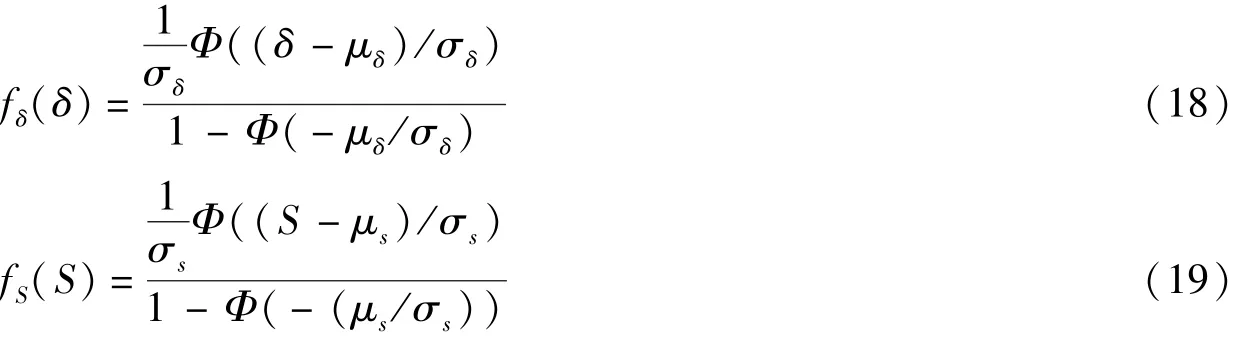
其中Φ(·)为标准正态分布的累积分布函数。 根据应力-强度干涉理论, 当应力S和强度δ相对独立时,结构可靠度计算公式为

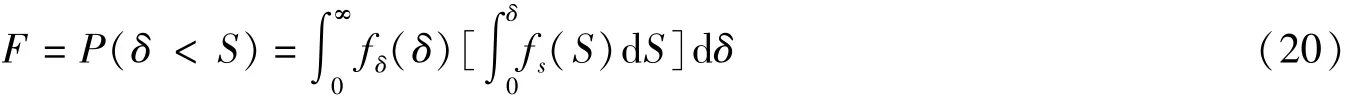
在执行飞行任务时, 机翼受到的气动力大小可通过式(1),式(2)计算。 在环境相差不大的情况下,气动载荷的作用过程可以用随机过程描述, 这里考虑泊松随机过程进行描述载荷作用次数随时间的变化过程。

令N(t)为时间(0,t)内载荷出现的总次数, 而且满足条件: 随机过程N(t)的状态只取非负整数值, 且N(0)= 0; N(t)为纯不连续的马尔科夫过程, 而且是一个独立增量过程。 考虑执行飞行任务时间为[t0,t1]的区间中载荷作用次数服从均值为λt 的泊松分布, 即对一切满足k≥t0, k+t≤t1的非负数k,t 都有

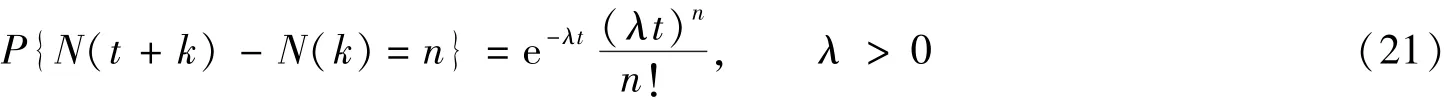
成立。 其中k 表示初始时间, t 表示作用时间, n 表示可能出现的载荷作用次数, 计数过程{N(t),t＞0}为满足速率为λ 的泊松随机过程。 载荷作用过程可用时齐泊松随机过程描述。 结合近年来的实际飞行数据分析, 当测试时间定在650 ～700 s 范围内时, 每次飞行过程中机翼受到的载荷作用总次数服从λ≈77的时齐泊松随机过程。

下面考虑在机翼强度退化明显时可靠性模型的建立。 假设有足够大的飞行器样本空间M, 每个样本无差, 且同时执行相同飞行任务。 由于载荷作用过程独立, 在确定初始强度后, 任意时刻的强度也确定,考虑执行飞行任务时间t, 可靠度为R(t)。 由于R(t)逐渐减小, 则在时刻t 可继续执行飞行任务的样本数量可表示为MR(t); 同理, 在t+Δ t 时刻能继续执行飞行任务的样本数量为MR(t+Δ t)。 在Δ t 足够小的情况下, 可以近似认为随机载荷在[t,t+Δ t)内出现的概率近似为二项分布, 所以载荷出现的概率近似为期望λΔ t。 根据可靠度定义可得

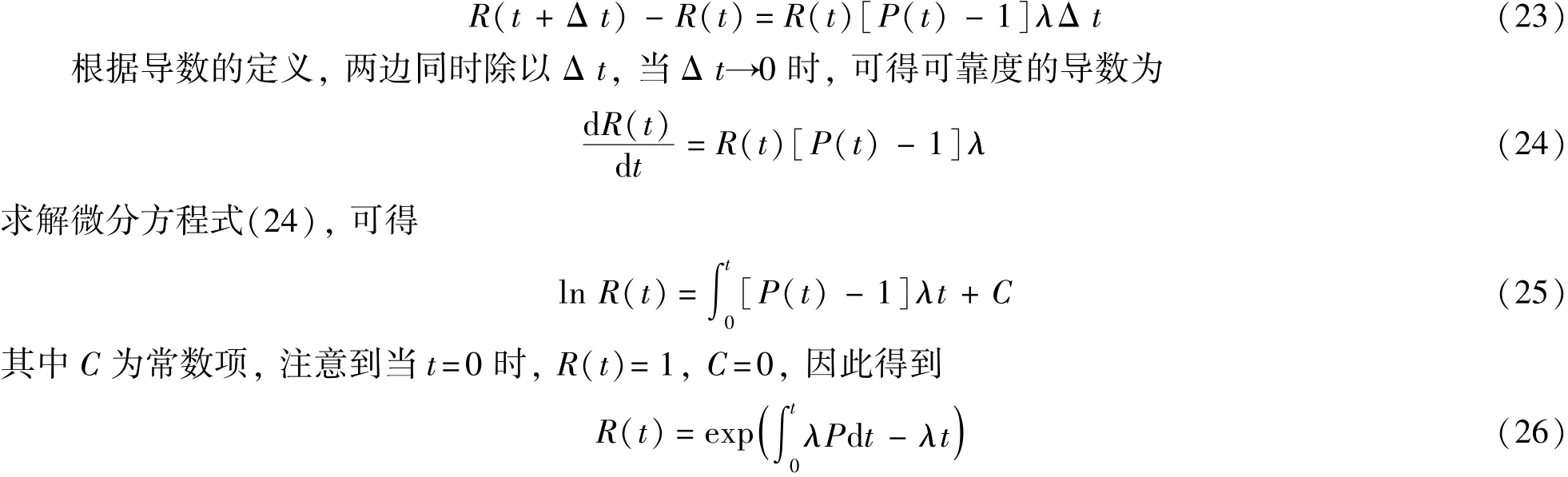
由于每个样本无差且相互独立, 根据无偏性理论可以得到单个样本的可靠度为式(26)。 式(26)可重写为

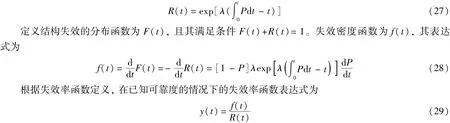
其为可靠度变化程度的函数, 将式(27)、 式(28)代入式(29), 可得在考虑材料退化率下机翼失效率函数为

平均失效间隔是可靠性模型的指标之一, 记为MMTBF, 指相邻两次故障之间的平均工作时间, 其数值与可靠度大小成正相关, 具体计算如下

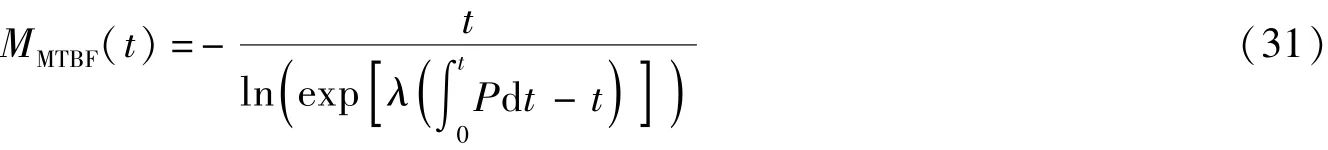
其数值伴随着强度退化而变化, 其反映了结构的时间质量, 是体现结构在规定时间内保持功能的一种能力。

综合R(t),f(t),y(t)和MMTBF即得到了机翼动态可靠性的模型, 也分别表征了动态可靠性的4 个指标。

3 近空间飞行器机翼可靠性分析

为验证所建模型的正确性和合理性, 笔者对计算结果进行仿真分析。 考虑近空间飞行器的高超声速飞行过程: 载荷作用总次数服从λ≈77 的时齐泊松随机过程; 机翼翼根受到的应力载荷服从参数为μs=110.34 Mpa, σs=46.27 Mpa 的截尾正态分布; 镍基合金材料(500 ℃)的名义屈服强度服从参数为μr=283.51 Mpa, σr=12.51Mpa 的截尾正态分布。

考虑强度退化模型为指数退化形式, 则有δt,r=δexp(-ζt), 其中ζ 是退化指数。 根据镍基合金手册计算得到, 规定剩余强度为初始强度的90% 为临界寿命, 在载荷μs=110.34 Mpa, σs=46.27 Mpa 作用下材料临界寿命为138 000 次, 计算得到ζ=0.000 000 8。

1) 考虑强度退化与不考虑强度退化, 进行可靠性指标的对比分析(见图3)。

从图3 中可看出, 当考虑强度退化时, 机翼翼根的可靠度(见图3a)和失效概率密度(见图3b)较未考虑强度退化时下降更快, 失效间隔更短(见图3c), 失效率更大(见图3d)。 由于在实际飞行中, 结构强度退化由于激波干扰、 气动热等因素是不可避免的, 因此这里考虑强度退化的可靠性分析更符合实际, 若未考虑强度退化, 可靠性分析的结论可能是不准确的, 甚至是错误的。

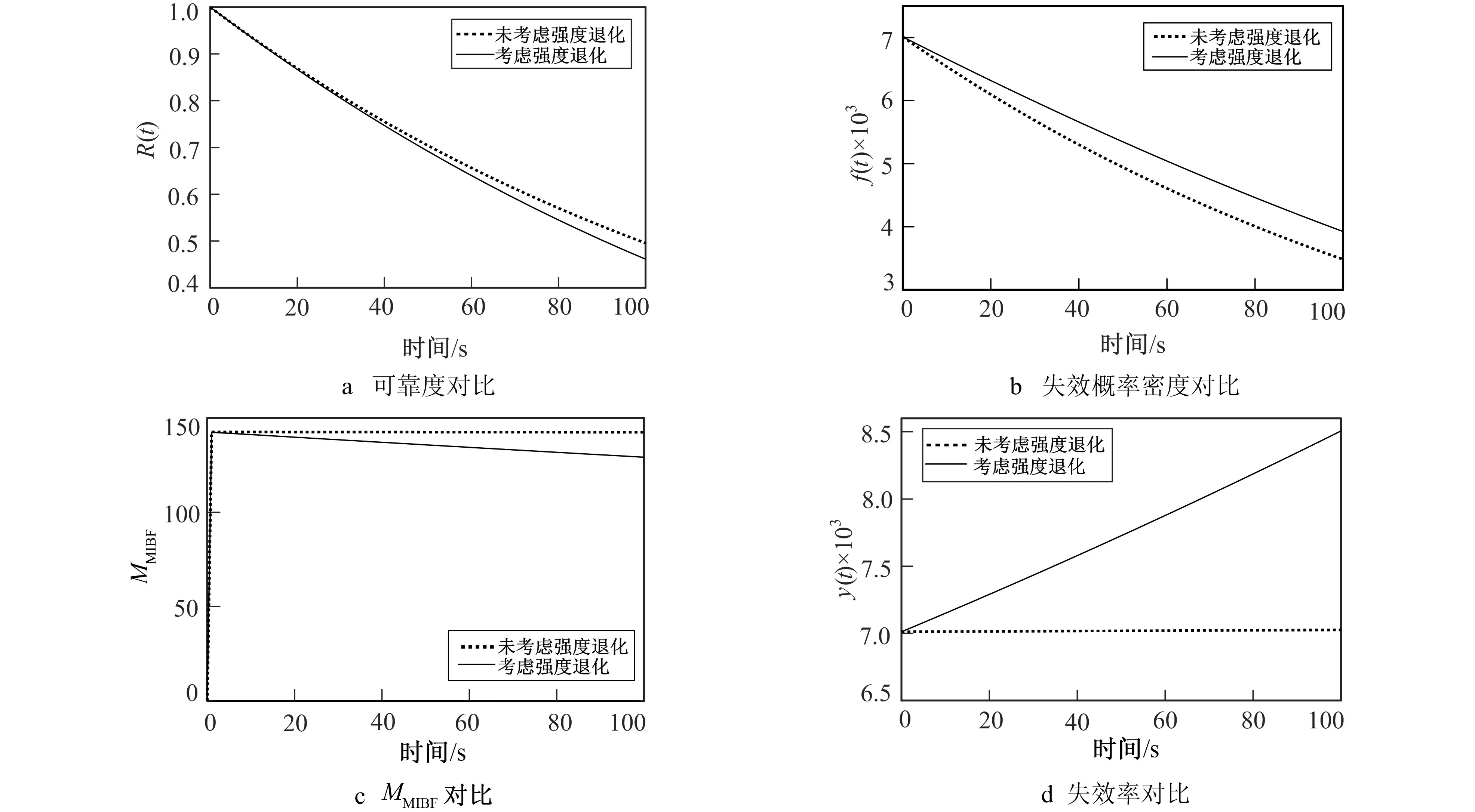
图3 考虑强度退化与未考虑强度退化可靠性指标分析对比Fig.3 Comparison of reliability indexes with and without strength degradation

2) 在考虑强度退化的基础上, 分析飞行动态对可靠度的影响。

首先进行MMach=7 和MMach=10 时的可靠度的对比分析, 其中α=5°,H=30 km。

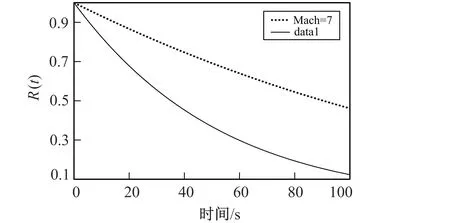
图4 马赫数变化时的可靠度的对比分析 Fig.4 Comparative analysis of reliability with Mach number change

马赫数、 高度和迎角变化时的可靠度的对比分析分别如图4 ～图6 所示。 从图4 中对比看出, 随着马赫数的增加, 近空间高超声速飞行器机翼翼根的可靠度有明显的下降。 仿真表明, 飞行速度的增加将降低飞行器结构的可靠度, 这与AIAA ( American Institute of Aeronautics and Astronautics)发布的实验数据[20]也是一致的。

其次, 分析高度H= 25 km,30 km 和35 km 时对可靠度的影响, 其中α=0°,MMach=7。

由图5 所示, 随着高度增加, 机翼翼根的可靠度也在逐步增加。 主要原因在于随着高度的增加, 大气密度逐渐下降, 使气动力Lw,Dw逐渐减小, 从而使机翼受到的载荷应力变小。

最后, 分析迎角α=-5°,2°,5°和10°时的可靠度的变化, 其中MMach=7,H=30 km。

从图6 可知,α=-5°和α=10°时机翼的可靠度下降得更快。 这说明在实际飞行中, 要尽量避免负迎角的出现和更大的迎角。 这主要是由于迎角的正负和大小与气动力密切相关, 负的迎角表征气动受力方向的改变, 而更大的迎角意味着结构所受的气动力和应力数值的增加, 因此负迎角和大迎角都会降低机翼可靠度。

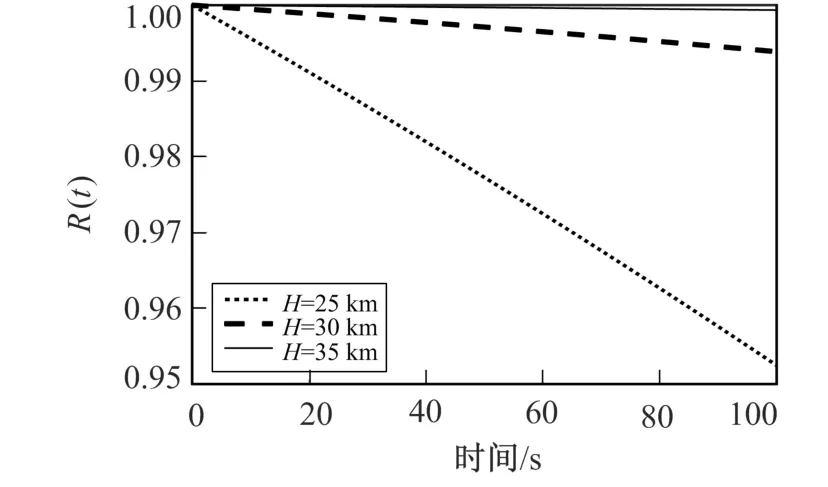
图5 高度变化时的可靠度的对比分析Fig.5 Comparative analysis of reliability with height change

图6 迎角变化时的可靠度的对比分析Fig.6 Comparative analysis of the reliability when the angle of attack changes

除此以外, 舵面偏转角、 滚转角和侧滑角等飞行动态都会对可靠度有一定的影响, 但与马赫数、高度和迎角相比, 它们的影响较小。 因此, 综合上述分析, 在实际飞行中若要保证飞行器的结构可靠性,应尽量避免飞行速度过快增加以及负迎角和大迎角, 条件允许的情况下适当增加飞行高度。

4 结 语

笔者对近空间飞行器机翼进行了受力分析, 并在此基础上建立了动态可靠性模型。 为验证所建模型的合理性, 分别分析了强度退化和飞行动态对可靠性的影响。 分析结果表明, 考虑强度退化得到的动态可靠性更符合飞行实际。 在近空间飞行范围内, 更快的飞行速度会降低机翼可靠度, 较低的飞行高度也会降低机翼可靠度, 而过大的迎角或负迎角的出现都会降低机翼可靠度。 通过对机翼可靠性的影响因素与动态特性进行定性地分析, 不仅可以为可靠性控制提供基础, 还可以为飞行器结构可靠性设计提供有价值的参考依据。