冰雪条件下高速公路可变限速方法

姚冬冬, 马 林, 陶鹏飞, 于丽梅, 吴 丛, 孔彩华

(1.吉林省交通科学研究所 科研开发中心, 长春130012; 2.吉林大学 交通学院, 长春130022;3.云南开放大学 教务处, 昆明650599)

0 引 言

我国北方地区冬季高速公路常受到冰雪天气影响, 运行效率严重下降。 现阶段我国高速公路管理部门在应对冰雪天气时, 常用措施是封路和通告限速。 封路会造成路段封闭并丧失功能, 通告限速通常是以固定限速方式执行, 这种管理模式难以满足大范围、 交通状态变化较快的道路环境需求。 在冰雪条件下, 路面状态变化较快, 为提升行车安全性的同时提高道路通行效率, 需依据实时路况准确及时调整限速值。

关于冰雪天气对道路通行影响的研究成果较为丰富。 李松龄等[1]运用车辆动力学理论对不同平曲线上车辆进行仿真分析, 并给出限速建议值。 朱兴琳[2]研究了包括冰雪天气的冬季灾害天气对高速公路的影响, 建立了基于安全距离的限速模型。 Tsapakis 等[3]对比了不同程度雨雪天气对城市路网各区域行程时间的影响, 并提出应急管理方法。 Xing 等[4]以快速路雪天数据拟合自由流速度, 并得出速度和流量的关系模型。 Rakha 等[5]研究了冰雪路面的货车特性, 采用仿真软件建立货车爬坡性能曲线, 给出爬坡车道临界坡长指标。 此类研究为冰雪条件下道路管理控制提供了理论依据。

可变限速作为一种较新的控制手段, 近年来较多出现在高速公路管理的研究中。 张存保等[6]对高速公路关联施工区交通特性进行分析, 建立了关联施工区可变限速协调模型。 吴德华等[7]针对宏观交通流模型(metanet)在预测交通拥堵路段时的缺陷, 提出高速公路可变限速修正模型, 有效降低了交通事故率。 王磊等[8]建立了基于事故损失的高速公路可变限速控制方法, 有效改善了高速公路运行状态。 张珊等[9]针对高速公路在雾天环境下的可变限速进行研究, 提出考虑交通流运行状态和驾驶员遵从度等因素的可变限速方法, 有效提高了雾天环境高速公路运行效率。 这些研究说明了高速公路在特定条件下实施可变限速的重要性与必要性。

综上所述, 对冰雪条件下道路的研究主要集中在影响分析与特定环境限速值的选取, 而对高速公路可变限速研究的重点放在了施工瓶颈区等特殊区段上, 总体尚缺乏针对我国冬季寒冷地区高速公路特点的可变限速研究。 笔者在上述研究基础上, 针对冰雪条件高速公路提出可变限速方法, 根据冰雪条件道路特性动态调整限速值, 从时间和空间角度对限速值进行优化, 从而达到提高冰雪条件下高速公路通行效率和安全性的目的。

1 冰雪条件高速公路可变限速机理

可变限速基本原理如图1 所示。 根据实际路况划分出限速区段, 并布设检测器与可变限速指示牌。主控系统根据检测器检测到的实时交通状态数据, 生成各个区段限速值, 并通过可变限速标志牌显示。当可变限速应用于瓶颈区段优化时, 检测系统一般以流量检测为主, 在本文中, 考虑到冰雪条件对道路交通状态的影响, 检测器主要用于检测雪况。 现阶段已存在用于检测路面雪况的检测器, 包括温度、视频和红外光谱检测等, 通过检测道面状态、 温度与气象条件等, 判断路面冰雪状态。

图1 高速公路可变限速示意Fig.1 Variable speed limit control in freeway

冰雪条件可变限速框架如图2 所示, 包括冰雪检测、 主控和指示系统。 主控系统是实现可变限速的核心部分, 由4 个模块组成: 1) 最大安全速度生成模块; 2) 限速值生成模块; 3) 限速值校正模块;4) 冰雪条件路况预测模块。 它们分别负责最大安全速度与限速值生成、 可变限速值校正以及冰雪天气路况预测。 冰雪条件路况预测的作用是保证限速值在时间维度校正环节的完整性, 以及检测系统出现故障时的数据补充, 可变限速值生成主要依靠实时检测数据源。

图2 可变限速系统框架Fig.2 Variable speed limit system framework

2 冰雪条件高速公路可变限速模型

2.1 最大安全速度

最大安全速度指行驶车辆在保证安全性前提下所能提供的最大速度。 高速公路车流为连续流, 其最大安全速度主要取决于道路线形与路面状态。 在冰雪条件下, 路面附着系数随雪况变化而改变, 道路线形则取决于实地条件, 同时由于道路附着系数降低, 车辆行驶稳定性下降, 制动距离大幅上升, 因此必须低于常速行驶。 不同雪况对应不同道路附着系数如表1 所示。

表1 冰雪路面对应附着系数Tab.1 Adhesion coefficients in different road conditions

车辆附着系数分为横向与纵向系数, 分别保证车辆行驶时的横向与纵向稳定性, 前者应用于平曲线道路的速度计算, 后者应用于直线道路的速度计算, 二者关系为

其中u为附着系数,uh为横向附着系数,uv为纵向附着系数。 根据文献[1]取uv=0.8u, 则uh=0.6u。直线道路以车辆停车视距为标准进行最大安全速度计算, 停车视距为

其中S为停车视距,lr为反应距离,ld为制动距离,ls为最小安全距离, 取ls=5 m。lr与ld分别为

其中vs为最大安全速度,tr为反应时间, 取tr= 2.5 s, g 为重力加速度, 取g = 9.8 m/ s2,i为纵坡。 由式(2) ～式(4)可得速度为

平曲线道路上, 以车辆转弯稳定性为标准进行最大安全速度计算, 临界稳定时

其中R为圆曲线半径,m为车辆质量, G 为引力常数,ih为超高。

特别地, 缓和曲线曲率介于相邻直线及圆曲线之间, 其限速值也介于二者之间, 在实际工程中可将缓和曲线与相邻圆曲线部分划归相同限速段。

2.2 合理限速值选取

直线道路安全速度由停车视距得到, 确保车辆在发现障碍物时安全停下, 因此可直接作为限速值。考虑到驾驶员特性, 限速值应取10 的整倍数, 则直线限速值为

其中mod 为求余运算。

曲线道路安全速度基于侧向力得出, 它仅确保车辆在临界条件不发生侧滑, 但无法保证车辆稳定舒适的行驶, 因此曲线道路限速值须要在安全速度基础上进行折减。 曲线道路最大安全速度是保证车辆横向稳定的临界值, 在减去速度余量后可认为是允许行驶的最大速度, 但该速度仍不适合作为限速值。 研究表明, 85% 位车速作为限速值事故率最低, 故将85% 位车速其作为限速标准, 限速值为

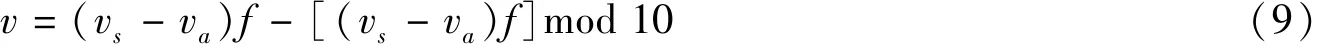
其中va为安全速度余量, 取5 km/ h, f 为85% 位车速与最大速度之比。

笔者采用Whitemud Drive 高速公路可变限速数据进行f 值获取。 Whitemud Drive 是加拿大Edmonton市内一条高速公路, 长28 km, 基本限速为80 km/ h。 路段装有检测器并采用可变限速控制。 由该数据集获取最大速度与85% 位车速的关系如表2 所示。 可以看到, 可变限速控制条件下, 不同点位与车道的f在0.65 上下波动, 笔者取数据集均值f=0.664 4 作为默认值, 实际应用中, 该值可由可变限速控制路段实测数据得出。

表2 高速公路实测f 值Tab.2 Measured f value in freeway

2.3 基于时空特性的可变速度校正

可变限速时空关系如图3 所示。

图3 可变限速时空关系Fig.3 Variable speed limit time-space relationship

为保证车辆行驶的稳定性, 相同时段内, 相邻限速段的速度差必须保持在一定范围内。 同一限速段在相邻时段的速度差也必须保持在一定范围内, 则时段t 路段i 的速度约束为

其中vi(t),vi(t-1),vi(t+1)分别为路段i在时段t-1,t,t+1 的速度(vi(t+1)属于未知量, 需要通过预测求得,预测方法见2.4 节),vtu,vtd,vsu,vsd分别为相邻时段速度增加、 减少阈值和相邻限速段增加、 减少阈值。 根据文献[10], 分别取20 km/ h、20 km/ h、10 km/ h、20 km/ h。 速度校正步骤如图4 所示。

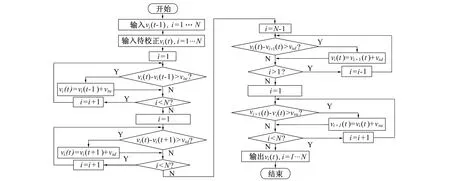
图4 速度校正流程Fig.4 Speed correction process

2.4 模糊控制冰雪路况预测

在时段限速校正时, 未来时刻限速只能通过预测得到, 以预测值为参考, 对当前时段限速值进行校正,防止其与预测值之差大于vtd。 笔者通过模糊控制器预测未来路面雪况, 进而预测限速值。 模糊控制是以模糊数学为基础的控制方法, 对于复杂、 变量过多且难以准确描述系统状态的问题具有较好的效果。 主要包括: 定义变量、 模糊化、 知识库、 逻辑判断及反模糊化。 笔者采用3 个状态变量与一个控制变量, 状态变量的定义与模糊化如表3 及图5 所示。 控制变量, 即预测雪况的参数与当前雪况状态变量相同, 仅存在变量符号的差异, 控制变量符号首字母由X 转换为P。 知识规则库如表4 所示, 反模糊化采用重心法。

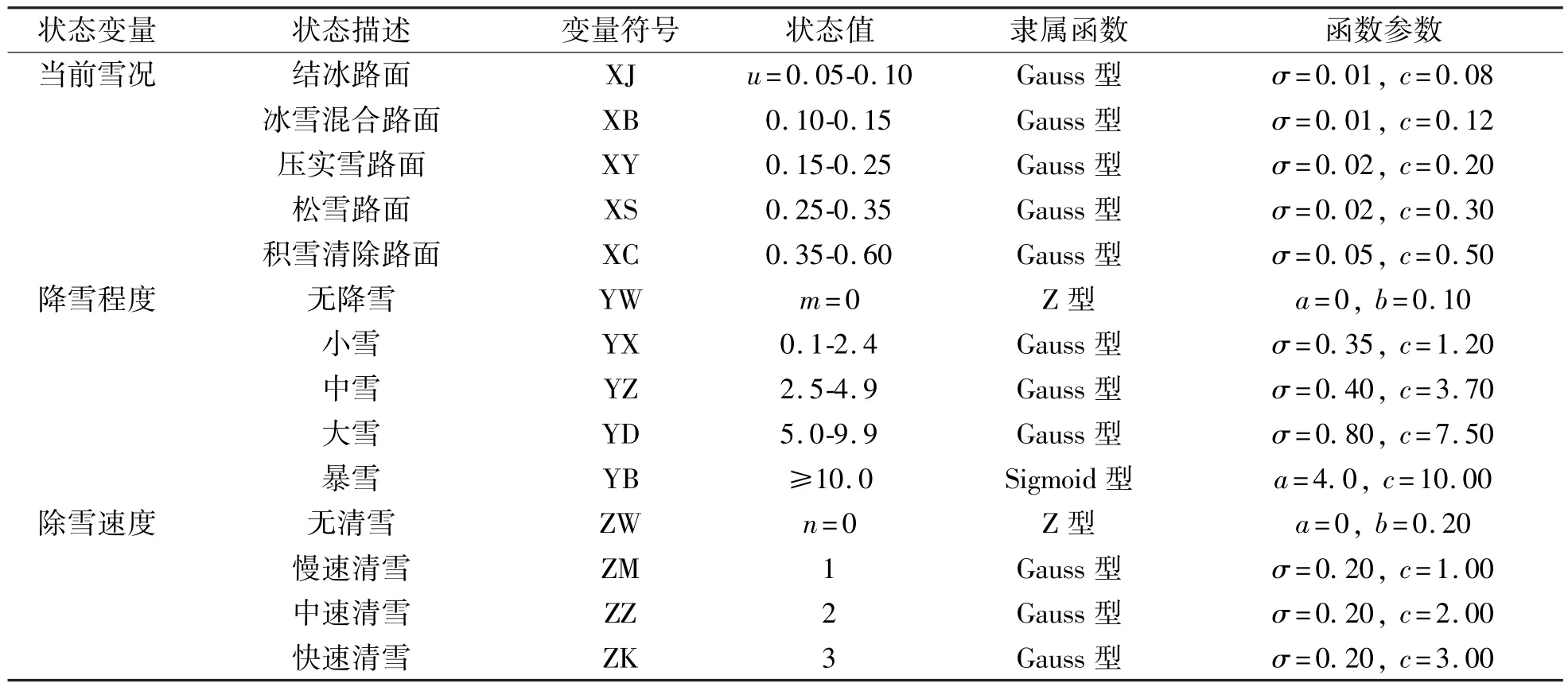
表3 变量定义与模糊化Tab.3 Variable definition and fuzzification

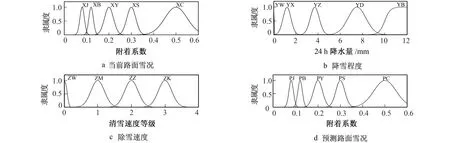
图5 隶属度函数Fig.5 Membership functions

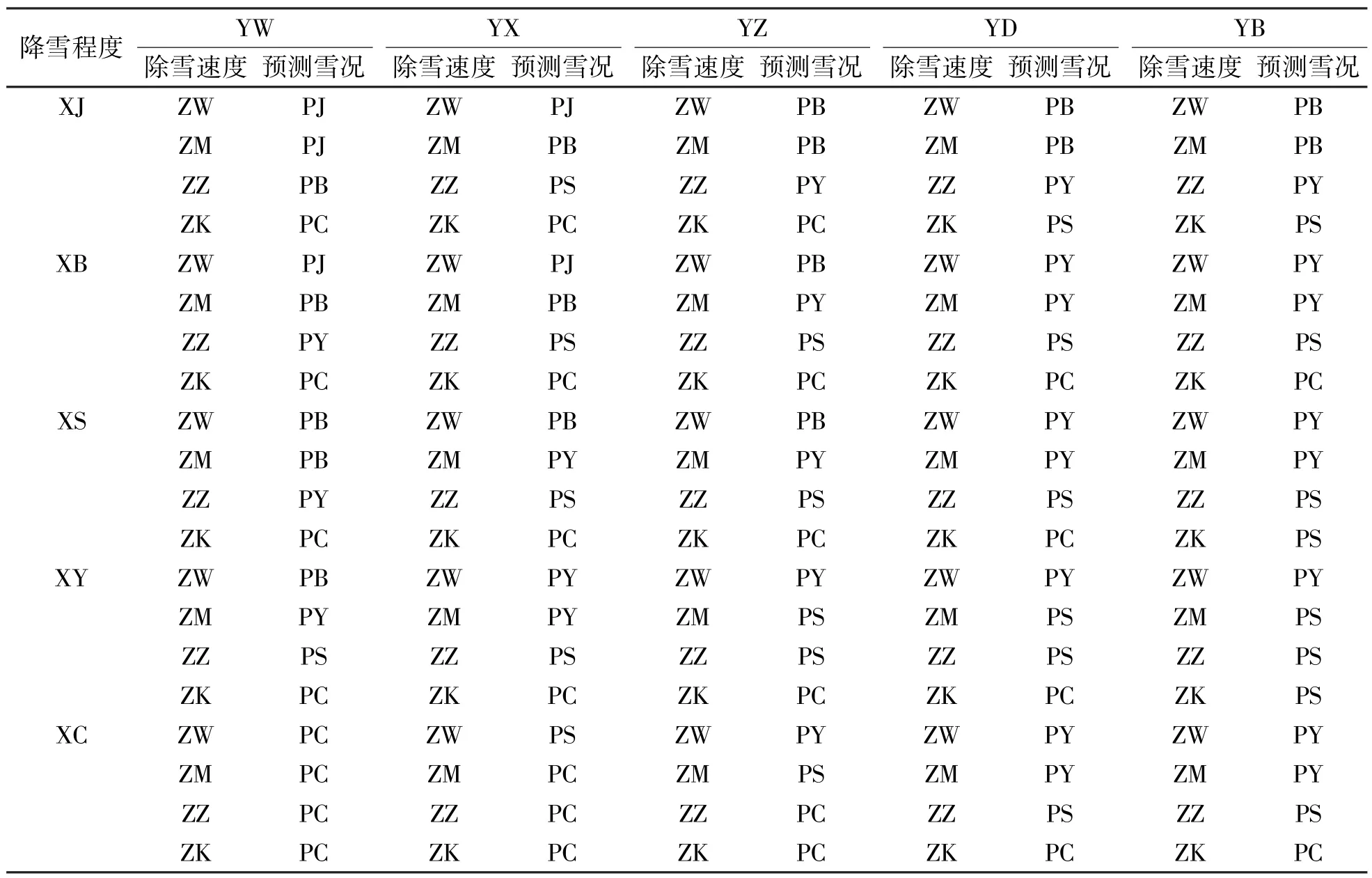
表4 模糊规则库Tab.4 Fuzzy rule base

3 仿真验证

3.1 仿真说明

现阶段我国高速公路尚不具有系统的可变限速控制段, 可变限速效果需要仿真实验验证。 仿真段采用上述Whitemud Drive 公路, 如图6 所示。 行驶方向由西向东, 首段为缓冲段, 用以车辆常速驶入。 限速段A 与D 无急弯, 可近似看作直线, 限速段B 与C 分别有一明显转弯, 其曲线半径分别为400 m与300 m, 超高均为0.05。

仿真通过Vissim 软件com 接口实现, 以6 h 为仿真时间, 第1 h 为仿真预热期, 后5 h 天气仿真状态设定如表5 所示。 根据仿真条件与上述模型计算所得可变限速方案如表6 所示。 数据采集间隔为1 h。 仿真采用两个对照组, 对照组Ⅰ为全线30 km / h 限速, 对照组Ⅱ为全线40 km / h 限速,实验组Ⅲ为可变限速。 由上述安全速度可知, 组Ⅰ与组Ⅲ限速不超过安全速度, 而组Ⅱ在第5 h中有限速段的速度超过安全速度, 因此该时段为封路清雪期, 在清雪期后, 即第6 h 全线恢复基本限速。

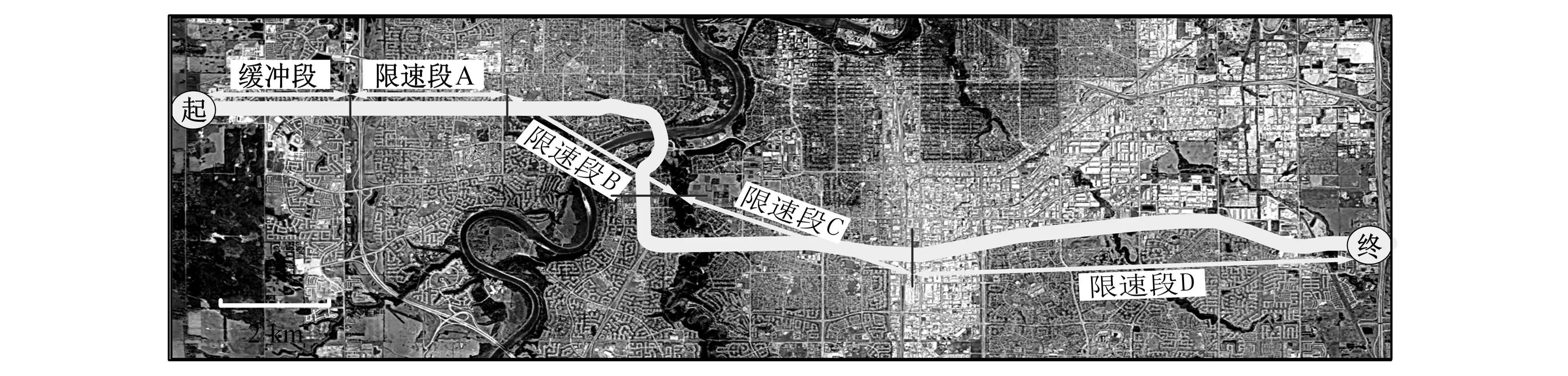
图6 仿真路段示意Fig.6 Simulation section

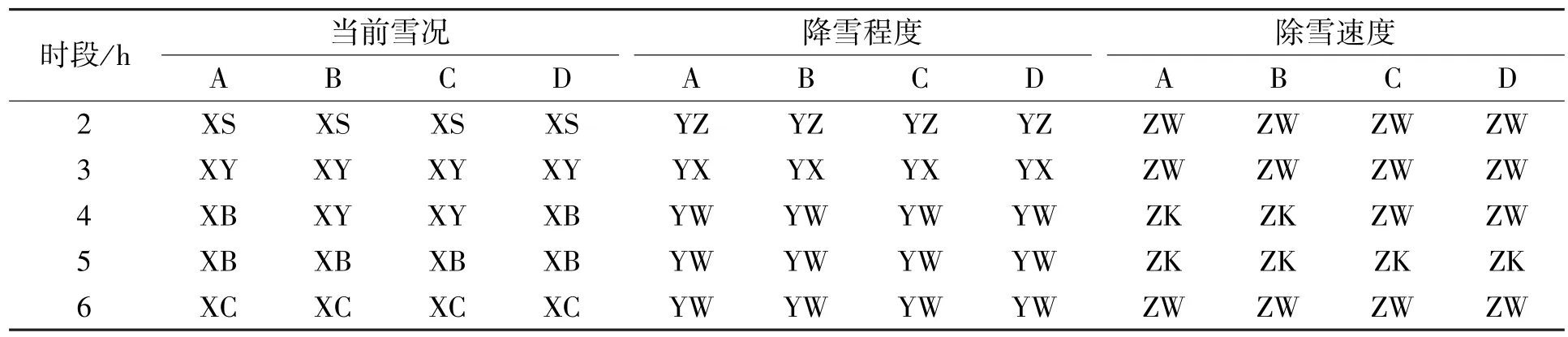
表5 仿真路段天气状态Tab.5 Weather conditions in simulated road

表6 可变限速方案Tab.6 Variable speed limit scheme 单位: km/ h

3.2 仿真结果对比与分析

由表7 可知, 在各个时段, 实验组Ⅲ的各个限速段延误均明显低于对照组Ⅰ, 说明可变限速相对于全线固定限速, 对延误具有明显的优化作用。 对照组Ⅱ在除雪前期, 部分限速段上延误略低于组Ⅲ, 但整体上延误高于组Ⅲ并低于组Ⅰ, 说明较高限速值的固定限速可以一定程度上降低延误, 但延误优化效果仍低于可变限速。 组Ⅱ在第6 h 时延误低于组Ⅰ与组Ⅲ, 说明在封路除雪后, 道路通行状况得到改善。但是, 封路除雪期间会造成车辆无法通行, 从另一角度降低道路运行效率。

表7 仿真路段延误对比Tab.7 Delay comparison in simulation section 单位: s/ veh

由表8 可知, 组Ⅰ与组Ⅲ在仿真期间通过车辆数相近, 且均高于组Ⅱ, 这是由于组Ⅱ封路期间禁止通行, 封路除雪结束后通行能力才转变为三者最高。 由此可见, 冰雪条件下可变限速相对于全线低限速而言, 对延误具有明显降低作用; 相对于全线较高限速而言, 可以在总时段内通过更多车辆, 具有明显的优化作用。

表8 仿真路段流量对比Tab.8 Traffic flow comparison in simulation section 单位: veh

4 结 语

针对冰雪条件下高速公路车辆通行效率及安全性降低的问题, 建立考虑冰雪条件与线形条件的可变限速模型, 通过仿真与日常限速手段进行比较, 验证了可变限速方法对高速公路延误与通行能力的优化效果。 笔者提出的可变限速框架中, 路面雪况的模糊控制逻辑库主要依靠专家决策, 这需要对冰雪路面特性更加深入的研究以提高其准确性。