构造圆解决数学问题例析

福建 童其林

《普通高中数学课程标准(实验)》的总目标中提出“提高提出问题、分析和解决问题(包括实际应用问题)的能力”，《普通高中数学课程标准(2017年版)》新增加了“发现问题的能力”，并且整体上升到问题解决“四能”的层面，这是目标上的一个变化，也给高中数学教学带来了新挑战.例如发现问题是指发现什么问题呢？是发现变化中的不变量，还是发现几何问题可用代数的方法解决，等等.下面笔者针对一些数学问题中通过发现隐性圆可以快速求解问题，或突破解题瓶颈的方法和大家进行分享.

一、向量问题中构造圆

( )

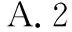
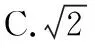
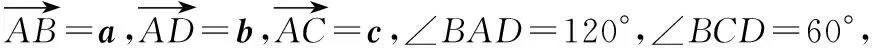
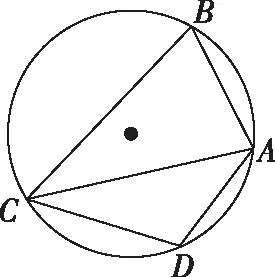
点评：向量是有方向的量，有明显的几何意义.构造适合已知条件的直线、三角形、圆等，是快速求解的一个方法.

二、解析几何中构造圆

例2过点(0,2)作直线x+my-4=0的垂线，垂足为Q，则Q到直线x+2y-14=0的距离最小值为

( )

A.0 B.2

解法一：设P(0,2),R(4,0),

直线l方程为x+2y-14=0，

则直线PR的方程为x+2y-4=0，且直线PR∥l,

过点Q作QM⊥PR于点M，延长MQ交l于点N,

设d=|QN|=|MN|-|QM|，

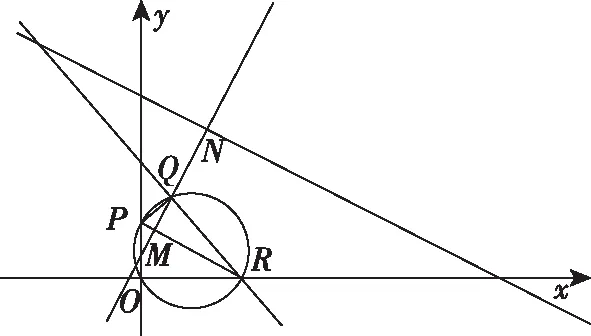
解法二：点Q在以PR为直径的圆上(除去圆与x轴的交点)，

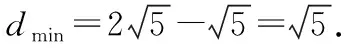
点评：解法1利用均值不等式求解，解法2发现点Q在以PR为直径的圆上(除去圆与x轴的交点)，从而快速找到解题思路.

例3已知实数a,b,c成等差数列，点P(-3,0)在动直线ax+by+c=0(a,b不同时为0)上的射影点为M,若点N的坐标为(2,3)，则线段MN的最大值是________.

解析：因为a，b，c成等差数列，所以2b=a+c，方程ax+by+c=0可以变形为2ax+2by+2c=0,则有2ax+(a+c)y+2c=0,整理为a(2x+y)+c(y+2)=0.

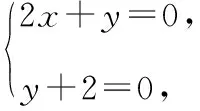
因此直线ax+by+c=0恒过定点Q(1,-2).

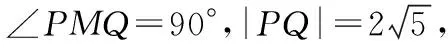
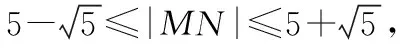
点评：注意直角三角形的外接圆以斜边的中点为圆心，这是隐性圆的一个特征.

例4在平面直角坐标系中，已知点A(4，0)，B(-6，0)，点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为________.

解析：构造含有90°圆心角的⊙P，则⊙P与y轴的交点即为所求的点C．注意点C有两个．

设线段BA的中点为E，∵点A(4，0)，B(-6，0)，∴AB=10，E(-1，0)．

以点P为圆心，PA(或PB)长为半径作⊙P，与y轴的正半轴交于点C，

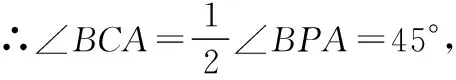
过点P作PF⊥y轴于点F，则OF=PE=5，PF=1，

所以OC=OF+CF=5+7=12，

所以点C坐标为(0，12).

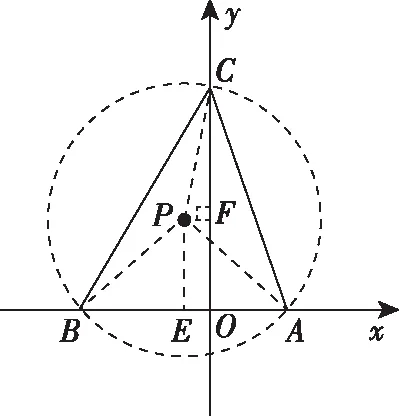
(2)如图所示，在第三象限可以参照(1)进行同样操作，同理求得y轴负半轴上的点C坐标为(0，-12)．

综上所述，点C坐标为(0，12)或(0，-12)，

故答案为(0，12)或(0，-12)．

例5如图，等边三角形ABC的边长为a，两顶点A，B分别在x轴，y轴上移动，求第三个顶点C到原点距离的最大值和最小值.

解析：由于A，B两点均在运动，用常规方法解答比较繁难.不如来个“动静互换”，即把线段AB看作定线段，原点O作为动点，当O点运动时，由于要始终保持OA⊥OB，故动点O的轨迹是以AB为直径的圆，这样就把求动点C到定点O距离的最值问题转化为求定点C到动点O的距离最值问题.于是本题转化为平面几何中求圆外一点到圆上各点的距离最值问题，这种问题的解法非常直观，非常简捷.

点评：解决两个点或多个点变化的问题，首先可以让某个点固定，找出其中的另一个点变化的规律，这就是我们常说的“动静互换”思想，需要想象能力.

在涨跌循环的市场规律下，今年一个意外的干扰因素是非洲猪瘟疫情，对于禽类市场的提振较为明显。尤其进入10月份后，疫情发展较快，禁运令对于生猪市场影响进一步显现，禽类市场开始进入震荡上行的趋势，蛋鸡养殖盈利较可观。卓创资讯市场分析王爱丽认为，从鸡苗销量看，后期新开产蛋鸡的数量也偏少，一直到年底都是这样。十二月、一月整体供应都偏紧张，所以鸡蛋价格会维持在高位，行情偏好。

三、三角形问题中构造圆

( )

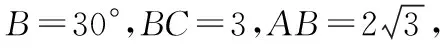
由AB2=BC2+AC2得∠C=90°.由对称性知BC与B′C′交点在AD上，如图.

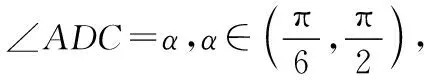
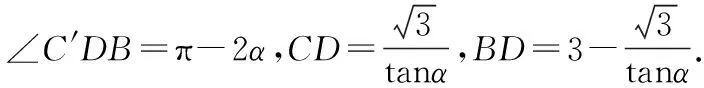
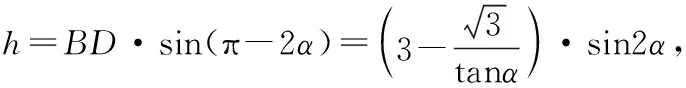
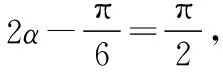
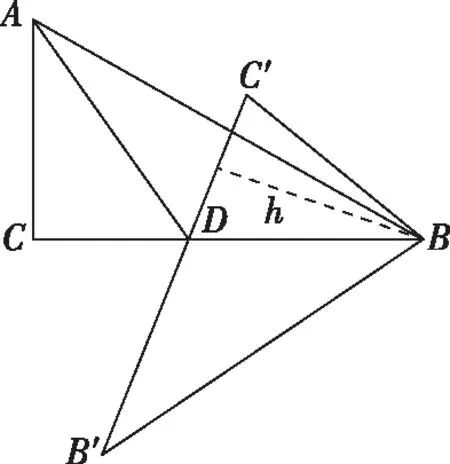
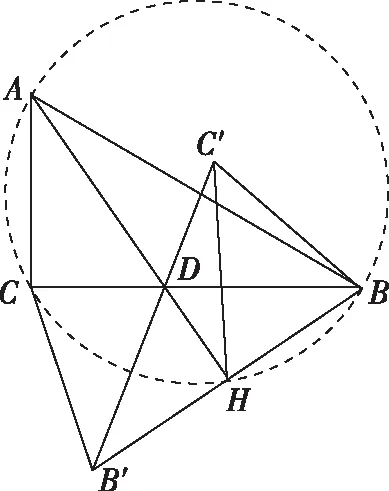
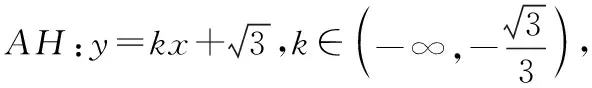
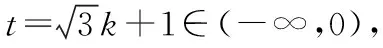
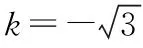
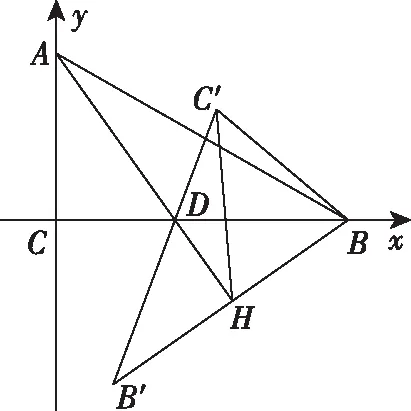
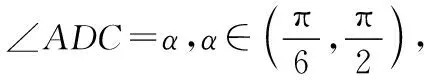
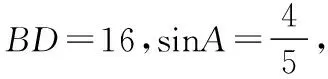
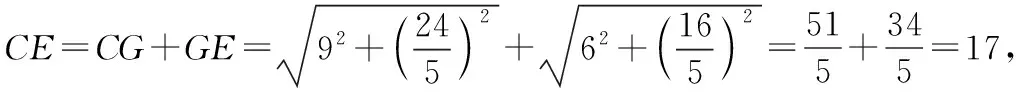
AC=CE+AE=27，故对角线AC的最大值为27.

点评：本题涉及较多的平面几何知识和解三角形知识，要注意点的轨迹在求几何最值问题中的应用，即在求解平面几何问题时要有轨迹意识.计算CE还有如下方法.

①建系法：如果以D为原点，DB所在直线为x轴，DC所在的直线为y轴建立直角坐标系，则C(0,9),E(8，-6)，得CE=17.计算量比前面的方法小一些.

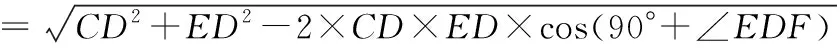
=17.

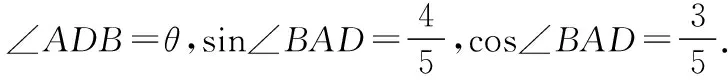
即AD=20sin(θ+∠BAD)=12sinθ+16cosθ.

在△ACD中，由余弦定理得，

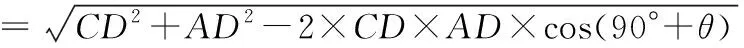
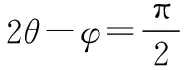
解法二体现了解三角形的基本解法——引入参数θ，将求距离最值问题转化为求三角函数的最值问题，需要一定的三角变换能力，有不小的运算量.相比之下还是解法1发现隐圆求解更简单.

实际上，出现隐圆的情况不只以上三种情形，在函数问题中，在复数问题中，在平面几何及立体几何问题中，都可能有隐性圆的情况.