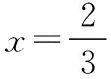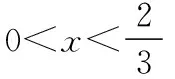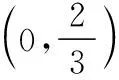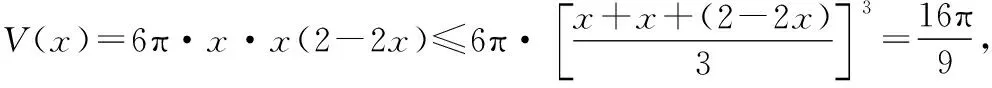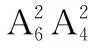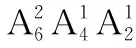“五育”并举 聚力育才—以“五育”为背景的高中数学题的求解策略
福建 汤小梅 郑金木
近三年的全国高考数学试题落实构建“德智体美劳”全面培养教育体系的要求,贯彻“五育并举”方针,突显数学学科特色,体现“五育”并举的育人价值,助力素质教育发展.体现德育、智育、体育、美育、劳动技术教育的有关考题,成为高考一道道亮丽的风景题,这类试题以丰富的真情实景或古代数学文化为载体命制与数学核心考点相结合的题目,意在考查数学建模、数学抽象、数据分析、直观想象、逻辑推理和数学运算的核心素养,值得重点关注.现聚焦2020年各省市的模拟题,欣赏以“五育”为背景的考题,供读者借鉴.
一、德育为先、立德树人
道德源于生活,以德育为背景的考题,多以民族精神、理想信念、道德品质、文明行为、社会公德、遵纪守法、心理健康等生活内容为题材,常以图、表、文并用的方式呈现,考查重点是用样本估计总体、随机抽样、离散型随机变量的分布列、期望与方差、数列、函数与导数等基础知识,难度一般为中档或中偏高档,意在考查数学建模、直观想象、逻辑推理和数学运算的核心素养.
【典例1】(2020·宜宾市叙州区第一中学校高三月考)为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

到班级宣传整理、打包衣物总计20人30人50人
(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用X表示所选志愿者中的女生人数,写出随机变量X的分布列及其数学期望.
【点拨】(1)利用分层抽样的抽样比,求出到班级宣传的志愿者与参与整理、打包衣物者的人数,利用古典概型的概率公式,即可得结果;(2)判断X服从超几何分布,利用超几何分布的概率和期望公式,即可得X的分布列与数学期望.
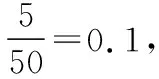
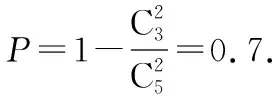
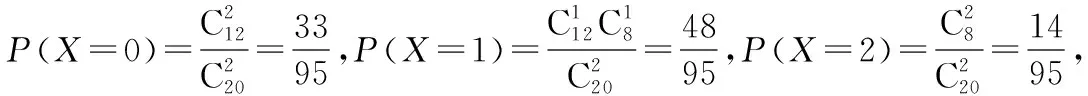
所以X的分布列为
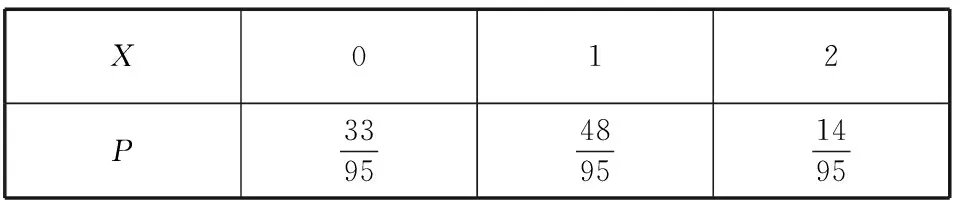
X012P339548951495
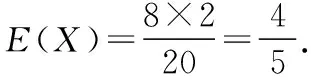

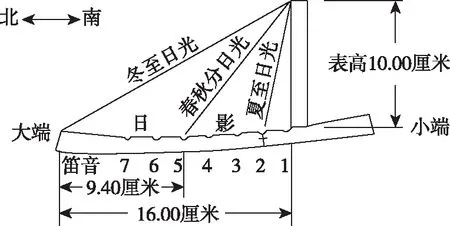
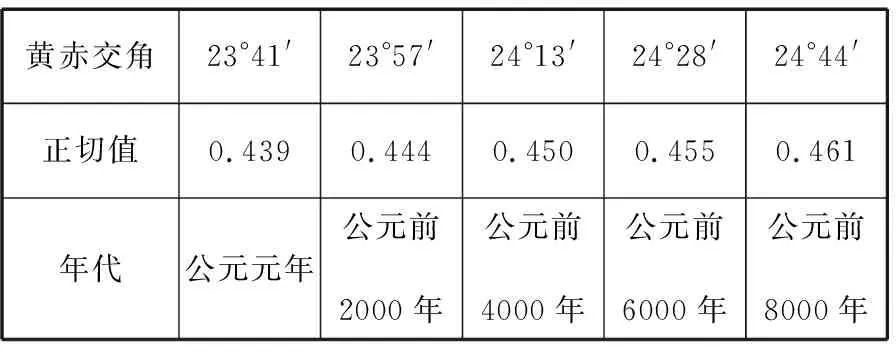
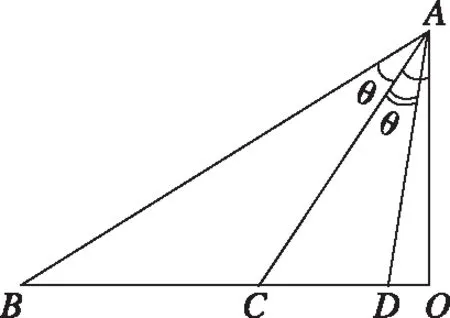
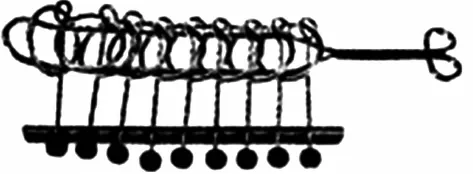
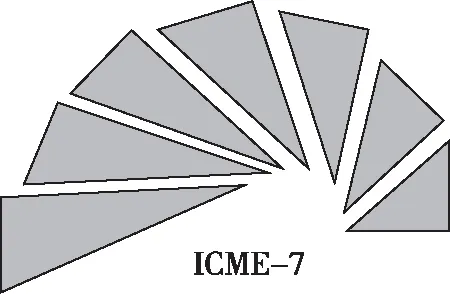
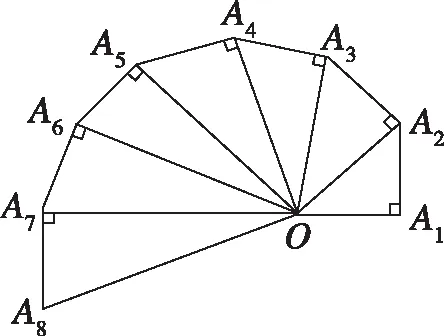
【典例2】(2020·河南省高三普通高等学校招生考试)2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为P(0 (1)求一天内被感染人数X的概率P(X)与a,p的关系式和X的数学期望; (2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有2位密切接触者,从某一名患者被感染,按第1天算起,第n天新增患者的数学期望记为En(n≥2). ①求数列{En}的通项公式,并证明数列{En}为等比数列; 【解析】(1)依题意得,被感染人数服从二项分布,即X~B(a,p), (2)①第n天被感染人数为(1+ap)n-1,第n-1天被感染人数为(1+ap)n-2, 当a=10,En=10p(1+10p)n-2.所以E6′=10×0.1(1+10×0.1)4=16, E6=10×0.5×(1+10×0.5)4=6 480,因为E6>E6′,所以戴口罩很有必要. 智育对于每个人的生活质量提高都有重要的意义,以智育为背景的考题,多以古代数学文化或实际社会生活中需要解决的问题为题材,主要考查高中数学的主干知识和非主干知识,难度可易也可难,突出考查数学建模、直观想象、逻辑推理、数据分析、数学抽象和数学运算的核心素养. 【典例3】(2020·福建省高三毕业班质检)上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角. 图1 图2 图3 由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表: 黄赤交角23°41'23°57'24°13'24°28'24°44'正切值0.4390.4440.4500.4550.461年代公元元年公元前2000年公元前4000年公元前6000年公元前8000年 根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是 ( ) A.公元前2000年到公元元年 B.公元前4000年到公元前2000年 C.公元前6000年到公元前4000年 D.早于公元前6000年 【方法点津】本题以我国传统文化“历律同源”为背景,借助出土文物骨笛的年代估算设计试题,考查解三角形、两角差的正切公式,体现了智育的素养导向.破解此类题的关键:一是准确理解题意,获取有效信息、合理运用图形;二是根据题意画出其示意图,示意图起着关键的作用;三是脱掉应用外衣,把所求的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理、解直角三角形等有关知识建立数学模型,认真运算,即可得出正确结果. 【典例4】(2020·云南省昆明市高三元月三诊一模)如图所示,九连环是中国的一种古老的智力游戏,它环环相扣,趣味无穷.它主要由九个圆环及框架组成,每个圆环都连有一个直杆,各直杆在后一个圆环内穿过,九个直杆的另一端用平板或者圆环相对固定,圆环在框架上可以解下或者套上.九连环游戏按某种规则将九个环全部从框架上解下或者全部套上.将第n个圆环解下最少需要移动的次数记为f(n)(n≤9且n∈N*).已知f(1)=1,f(2)=1,且通过该规则可得f(n)=f(n-1)+2f(n-2)+1,则解下第5个圆环最少需要移动的次数为 ( ) A.7 B.16 C.19 D.21 【解析】由已知f(3)=f(2)+2f(1)+1=1+2+1=4, f(4)=f(3)+2f(2)+1=4+2+1=7,f(5)=f(4)+2f(3)+1=7+8+1=16,故选B. 【方法点津】本题以古老的智力游戏“九连环”为背景,考查数列的递推公式等基础知识,体现了智育的素养导向.破解此类题的关键在于用慧眼去找寻“题眼”,用心灵去感受题意,如本例,题眼“f(n)=f(n-1)+2f(n-2)+1”,再利用科学合理地赋值运算,即可轻松获得结果. 体育活动,发展健康身心,增强体质、健全人格.以体育为背景的考题,多以体育竞技活动(掷铁饼、铅球、马拉松运动、游泳、射击等等)为题材,常以图、文并用的方式呈现,考查重点是三角函数、线性回归、独立性检验等基础知识,难度一般为中档,意在考查数学建模、直观想象、逻辑推理和数学运算的核心素养. ( ) A.1.012米 B.1.768米 C.2.043米 D.2.945米 【方法点津】本题以掷铁饼为背景考查弦长的探求,体现了体育教育的素养导向.求解的关键:一是读懂题意,明晰题眼,如掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,其实质就是两臂长与肩宽的和就是“弓”长;二是会利用公式,即会利用弧长公式,求出该弧所对圆心角;再利用余弦定理或勾股定理,求出弧所对的弦长. 【典例6】(2020·福建省厦门市期末质检)配速是马拉松运动中常使用的一个概念,是速度的一种,是指每公里所需要的时间,相比配速,把心率控制在一个合理水平是安全理性跑马拉松的一个重要策略.图1是一个马拉松跑者的心率y(单位:次/分钟)和配速x(单位:分钟/公里)的散点图,图2是一次马拉松比赛(全程约42公里)前3 000名跑者成绩(单位:分钟)的频率分布直方图. 图1 图2 (1)由散点图看出,可用线性回归模型拟合y与x的关系,求y与x的线性回归方程; (2)该跑者如果参加本次比赛,将心率控制在160左右跑完全程,估计他能获得的名次. (2)将y=160代入回归方程得x=5,所以该跑者跑完马拉松全程所花的时间约为42×5=210分钟. 从马拉松比赛的频率分布直方图可知成绩好于210分钟的累积频率为0.000 8×50+0.002 4×(210-200)=0.064.所以有6.4%的跑者成绩超过该跑者,则该跑者在本次比赛获得的名次大约是0.064×3 000=192名. “美”是景与情的交融,以美育人,让学生懂得美、爱美,提高学生审美和人文素养.以美育为背景的考题,多以提高学生审美和人文素养为题材,常以图、文并用的方式呈现,考查重点是三角函数、数列、立体几何等基础知识,难度一般为中档,意在考查直观想象、逻辑推理和数学运算的核心素养. ( ) 【方法点津】本题是利用古代数学文化“折扇”为背景命制与三角相结合的题目,把雅致秀气的“折扇”与扇形的面积相交汇,体现了美育的素养导向.求解的突破口是熟记扇形的面积公式,把半径相同的两扇形的面积比转化为两扇形的圆心角的比,再利用它们的圆心角的和为2π,即可得小扇形的圆心角的弧度数. 【典例8】(2020·云南省云天化中学期中)如图①是第七届国际数学教育大会(简称ICME-7)的会徽图案,会徽的主体图案是由如图②的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1,如果把图②中的直角三角形继续做下去,记OA1,OA2,…,OAn的长度构成数列{an},则此数列的通项公式为an=________. 图① 图② 【方法点津】破解此类以数学的美育为背景的数列题的关键:一是盯“题眼”和细“观图”,能从图中观察到数据的特征,如本题,从图形中能得到数列{an}的相邻两项的递推公式;二是会用定义,即会利用等差数列的定义,求出数列的通项公式. “劳”是实与理的交汇,引导学生崇尚劳动、尊重劳动,懂得劳动最光荣、劳动最崇高、劳动最伟大、劳动最美丽的道理,养成热爱劳动的习惯和本领,塑造劳动精神.以劳育为背景的考题,多以参加社会实践劳动、帮助别人、为集体做好事等生活内容为题材,考查重点是计数原理、立体几何、统计与概率等基础知识,难度一般为中档,意在考查数学建模、直观想象、逻辑推理、数学抽象和数学运算的核心素养. 【典例9】(2020·福建省高三毕业班质检)某学生到工厂实践,欲将一个底面半径为2,高为3的实心圆锥体工件切割成一个圆柱体,并使圆柱体的一个底面落在圆锥体的底面内.若不考虑损耗,则得到的圆柱体的体积最大值是 ( ) 解法二:同解法一,得V(x)=12π(x2-x3),0 【方法点津】本题以学生到工厂实践为背景考查圆锥内含圆柱、导数与最值、基本不等式等基础知识,引导学生积极关注并参与社会活动.在上述的两种解法中,解法一为常规解法,通过观察已知图形特征,设圆柱体的底面半径2x,快速找到圆柱的体积关于x的函数,借用“导数”的工具性,通过求导,判断函数的单调性,求出圆柱体积的最大值.注意隐蔽条件“自变量在实际意义中的取值范围”在解题中的应用.解法二,借用“三个正数的算术—几何平均不等式”,展现了基本不等式在最值求解中的威力和魅力,充分显示了解法的灵活性,实属巧思妙解,干净利落,意犹未尽. 【典例10】某校组织高三学生到“天生林艺”参加社会实践劳动,某天劳动安排有采茶,摘枇杷,摘草莓,锄草,植树,工艺品制作共六项活动可供选择,每个班上午、下午各安排一项活动(不重复),且同一时间内每项活动都只允许一个班参加,则该天甲、乙两个班的活动安排方案的种数为________. 【解析】根据题意,分三类安排活动: 【方法点津】本题以参加社会实践劳动为背景考查排列组合内容,体现了劳动教育的素养导向,求解难点是先“分类”后“分步”,还是先“分步”后“分类”,应视题意而定,如本题,需先分三类,在各类中,再分步解决;故在“分类”和“分步”的过程中,均要确定明确的分类标准和分步程序.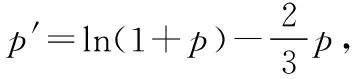
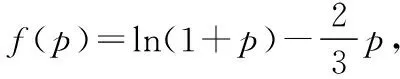
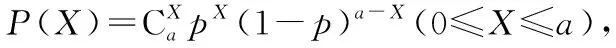
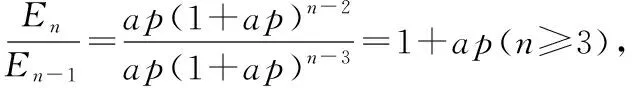
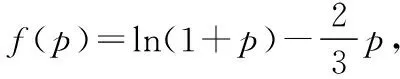
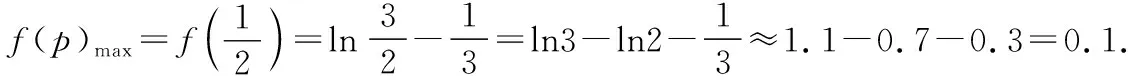
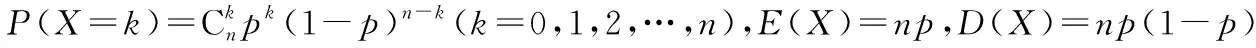
二、智育为核、提升能力



三、体育为基、享乐强体
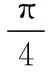

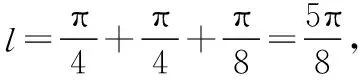
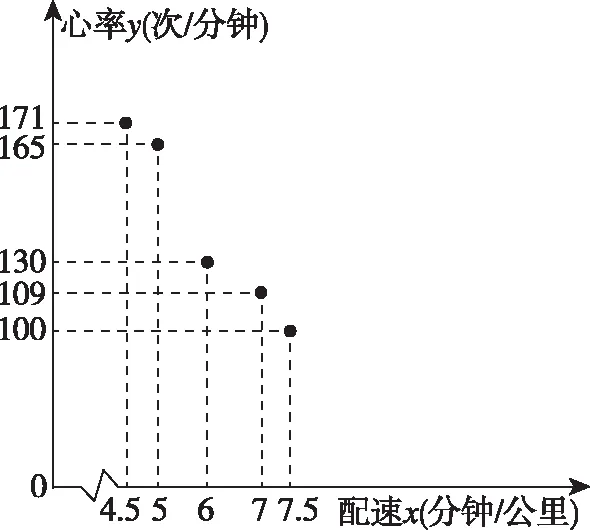
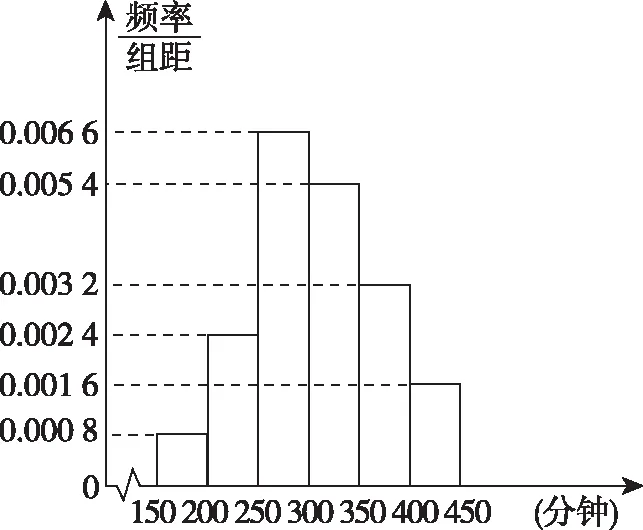
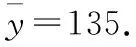
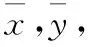
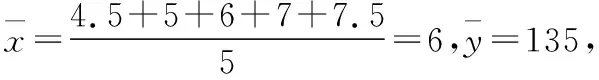
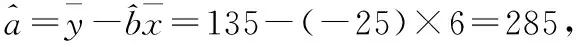
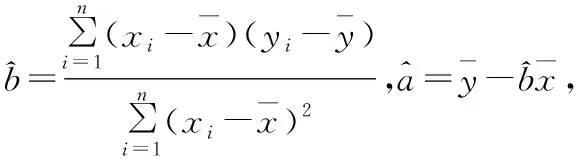
四、美育为魂、陶养身心

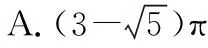
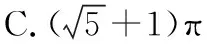
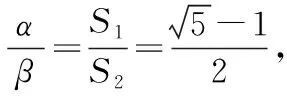

五、劳育为本,习得技能