数学建模核心素养在立体几何考题中的渗透

广东 李 虎

随着时代发展，教育更关注人的全面发展，更关注隐藏在知识背后的能力和素质的培养，新的数学课程标准中以培养学生的六个方面核心素养展开，其中数学建模核心素养强调数学应用，指向学生的综合能力和高阶思维，学生在考试中遇到往往丢分严重.本文就数学建模能力在立体几何考题中考查方法进行探究，以期指出学生的薄弱环节，指明今后培养的方向和路径.

一、无法完成从实际问题向数学问题转化的过程

题目：如图所示是一款热卖的小方凳，其正、侧视图如图所示，如果凳脚是由底面为正方形的直棱柱经过切割后得到，当正方形边长为2 cm时，则切面的面积为

( )

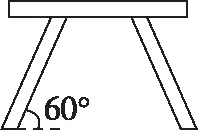
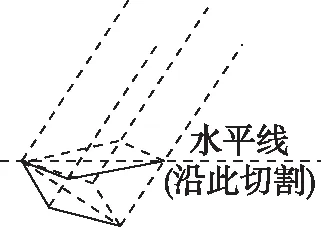
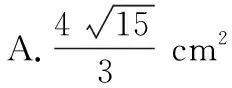
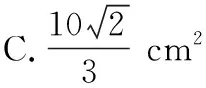
考情分析：如图1，我们将凳子的一条腿的直观图画出来，找到其正视图和侧视图对应的60°角，这里是本题的难点，大部分学生无法把这个60°角做出来，于是就无法完成从实际问题到数学问题的转化.因为学生在生活中可能没有仔细观察小方凳，甚至很多学生都没有见过小方凳,无法正确地构建模型.

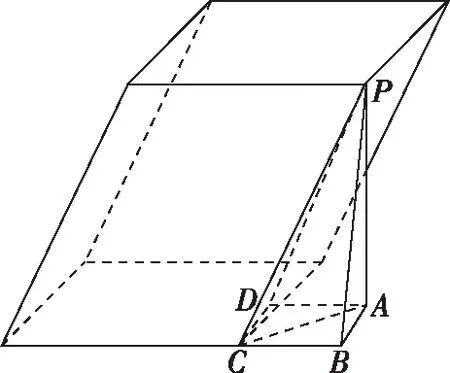
图1

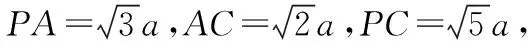
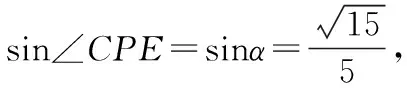
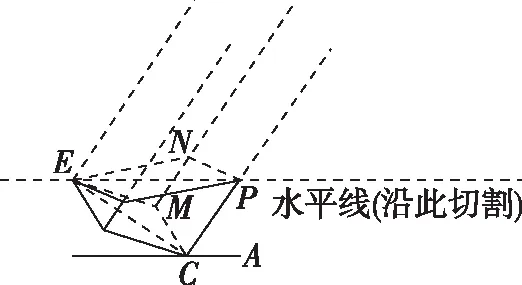
图2

考后评讲：在考后的评讲过程中，学生仍无法弄懂，为了帮助学生观察和思考，笔者还用一个近似正四棱柱的酸奶瓶子做了教具，如图3，以帮助学生思考，从课后的情况来看，评讲后学生仍无法将图1和图2之间如何联系起来想清楚.

图3

在评讲过程中，笔者发现还有一个难点学生无法突破，就是图2实际切割与图1如何联系起来.这个其实可以用面积射影定理来理解，把问题转化为找图2中切面与原正四棱柱底面的二面角问题，而二面角又可以转换为法向量所成的角∠APC，进而转化为棱PC与水平面所成的线面角，这样图1和图2就联系起来了.

进一步，如果EP不与水平线平行，凳腿将发生什么变化？

进一步引发学生思考，鼓励学生回家继续用用过的饮料瓶做实验，体会角度变化，带来的凳腿倾角的变化.

通过本题，学生无法正确建模的根源是学生对基本概念的理解不到位,这就要求平时教学中，要回归定义、定理、公理本身.

二、变量选择的合理性

(2014·浙江卷文·10)如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面的射击线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成角).若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值为

( )

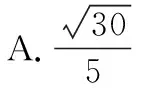
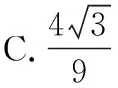
考情分析：思维的起点通常从问题开始，学生拿到此题后根据线面角的定义会做出如图所示辅助线，这里就会出现分水岭，有些同学选择假设CH=x，有些会选择BH=x(再讨论H在B的左侧或右侧)，有些同学假设PH=x，还有同学考虑建立空间直角坐标系，利用空间向量来做.这些方法都可以，但在实践中发现，假设PH=x是运算量最小的.那么，怎样确定假设引入哪个量作为变元呢？通常，首先要看是谁的变化引起的一系列变化，抓主要矛盾，其次选择的变元要能尽可能多的联系已知与要求解的问题，最后选择能直接反映动点运动状态的量最好，间接量一般会带来运算量的提升.这里，主要是P点高度的变化，引起的线面角的变化.

(2017·全国卷Ⅰ理·16)如图，圆形纸片的圆心为O，半径为5 cm，该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D,E,F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积(单位：cm3)的最大值为________.

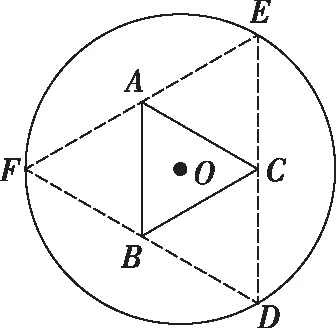
考情分析1：本题一系列的变化是由△ABC的变化引起，故可以直接设△ABC的边长为x，这是比较自然的一种想法.然后将体积写成x的函数关系式，从而转变为函数求最值问题.就自然产生了下面的解法1.

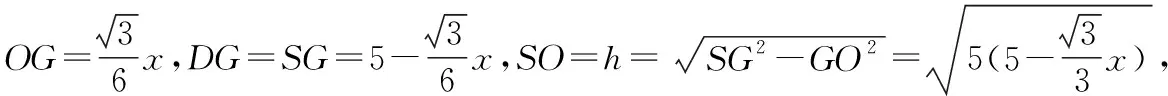
考情分析2：认真观察图形会发现，如果以O到BC的距离为变量，仍可以确定图形，此时正好在折叠后的图形中可以联系起体高与斜高的关系.这样假设运算更简洁，计算量会更小.就产生了下面的解法2.

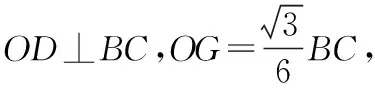
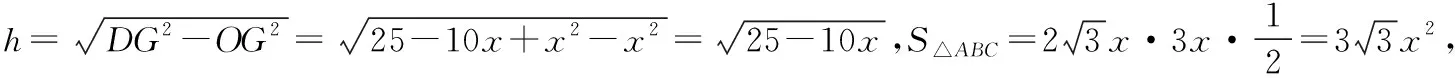
三、回归课本基本数学模型

这个结论学生基本都知道，但是深挖会发现，学生是一知半解.问题：(1)空间四面体是否一定有外接球？外接球唯一吗？(2)此四面体可以看成是一个长方体切下的一个角，那么这个四面体的外接球与长方体的外接球为什么是同一个球？(3)正四面体可以在正方体中截得，可以通过求此正方体的体对角线来求得正四面体的外接球直径,依据是什么呢？(4)过空间不共面的五点是否可以确定一个球呢？为什么？

在教学中，发现学生对以上问题模模糊糊，只是通过记忆记住了这个模型，在做题中不能灵活应用.比如我们编写一个这样的题目.

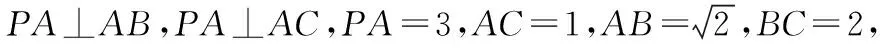
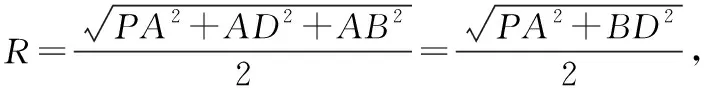
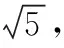
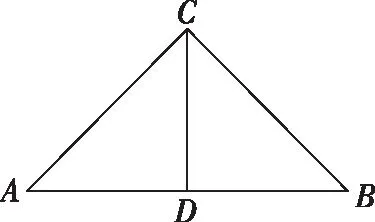
图1

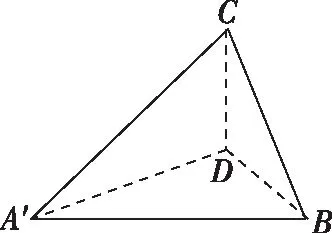
图2

高考题中关于球的切接问题的考查是非常频繁的，学生一定要吃透问题本质，在做题时才能如鱼得水.

四、结语