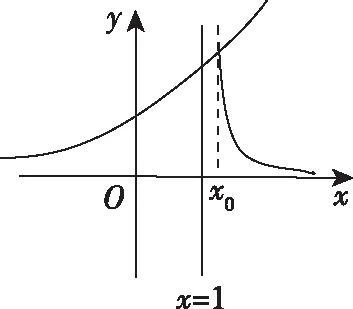
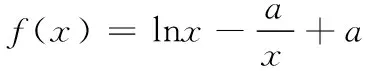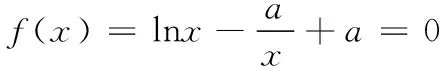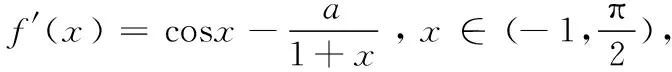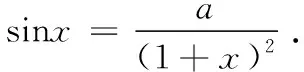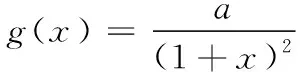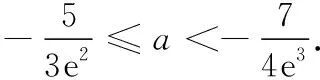从2020年一道函数隐零点模考题说起

安徽 李昭平

函数的隐零点问题在近几年的高考和模考中频频出现，成为试卷中一道亮丽的风景线.本文对2020年一道最新函数隐零点模考题进行思考和研究，揭示“一分为二”解题思想.并通过类比推广应用，深化解题思想方法，锤炼数学思维，提高复习效率.

1.题目

(2020年漳州高三适应性测试题)已知函数f(x)=lnx+ax+1有两个零点，则实数a的取值范围是________.

2.分析

本题函数f(x)中含有参数a，f(x)=0存在两个正实根，但无法求出，我们称这种函数具有隐零点.显然,此题若直接对f(x)求导，利用导数研究其图象与x轴正半轴有两个交点，又会涉及求f′(x)=0的根和对参数a的讨论，比较复杂. 这让我们联想到：能否直接将方程lnx+ax+1=0 “一分为二”成两个函数，利用函数y=lnx和y=-ax-1的图象的交点个数来处理呢？基于这种想法，得到下述解答.

3. 解答

函数f(x)=lnx+ax+1的定义域是(0,+∞)，

令g(x)=lnx，h(x)=-ax-1. 函数f(x)=lnx+ax+1有两个零点，即函数g(x)和函数h(x)的图象有且仅有两个公共点.

当a≥0时，两函数的图象只有一个公共点，不合题意,

当a<0时，由于直线h(x)=-ax-1经过定点(0,-1),而曲线g(x)在点(1，0)处的切线方程是y=x-1，也经过点(0,-1).因此直线y=x-1是直线h(x)=-ax-1的极限位置.

于是当-a<1，即-1

故实数a的取值范围是(-1,0).

4.结论

由上述解答，得到以下结论：设f(x)=g(x)-h(x),求f(x)的零点⟺f(x)=0的实数根⟺g(x)与h(x)图象交点的横坐标. 其中y=g(x)和y=h(x)是定曲线(含直线)或动曲线(含直线).对于含有参数的函数f(x)，或其导函数f′(x)，或f′(x)的导函数f′′(x)的零点问题，或不等式问题, 利用“一分为二”的思想将复合型函数方程f(x)=0，f′(x)=0，f′′(x)=0或不等式f(x)>0，f(x)<0,分成两条曲线y=g(x)和y=h(x)来处理，往往能化繁为简、化难为易, 融直观想象、逻辑推理和数学运算等核心素养为一体.下面结合典例介绍应用.

5. 应用

5.1 处理函数f(x)的隐零点问题

( )

即xlnx=-a(x-1).

令g(x)=xlnx,h(x)=-a(x-1)，

直线h(x)=-a(x-1)过定点(1,0),用导数知识可以画出定曲线g(x).

当a≥0时，两函数的图象在x∈[1,e]上只有一个公共点，不合题意.

点评：本题考查f(x)的隐零点，“一分为二”成两个函数g(x)=xlnx(定曲线)和h(x)=-a(x-1)(动直线)，则问题立即转化为定曲线与动直线的位置关系，利用数形结合、动静变化、极限位置，快速实现解题目标.注意对参数a的分类讨论和不等式g(e)≥h(e)中能取到等号.

5.2 处理函数f′(x)的隐零点问题

【例2】(2020年青岛市高三段考题)设a∈R,函数f(x)=ex-aln(x-1), 其中e为自然对数的底数. 试判断f(x)极值点的个数.

当a<0时，两函数的图象没有公共点，即函数f′(x)没有零点，此时f(x)没有极值点.

当a=0时，f(x)=ex，显然没有极值点.

当a>0时，如图，两函数的图象只有一个公共点，设其横坐标是x0.

显然，当x

当x>x0时，g(x)>h(x),f′(x)>0.

此时f(x)只有唯一极小值点.

5.3 处理函数f″(x)的隐零点问题

5.4处理不等式的证明问题

因此f(x)在(1,+∞)上单调递增，f(x)>f(1)=0.

再令g(x)=x-ex-1,则g′(x)=1-ex-1<0,g(x)在(1,+∞)上单调递减，g(x)

5.5处理不等式的整数解问题

【例5】(2020年皖江联盟联考题)已知函数f(x)=(2x+1)ex+1+ax(a∈R，e是自然对数的底数). 若有且仅有3个负整数x1,x2,x3，使得f(x1)≤0,f(x2)≤0,f(x3)≤0,则a的最小值是________.

显然，当a≥0时满足f(x)≤0的负整数x有无数个，因此a<0.

点评：本题是一次函数与指数函数的复合型函数，将不等式f(x)≤0“一分为二”成两个函数y=g(x)(定曲线)和y=h(x)(动直线)，则不等式的整数解问题立即转化为定曲线与动直线的位置关系，再列出相应的不等式组求解即可，要特别注意在何处取等号 .

5.6处理曲线的切线问题

则“过点P(1,t)存在3条直线与曲线y=f(x)相切”等价于“定曲线y=g(x)与动直线y=-t有3个不同的交点”．