“说题”引领教师专业成长——以2018年全国卷Ⅱ理科19题为例

贵州 袁小勇

相对于“说课”，“说题”还属于一个新鲜的事物.“说课”已经形成了一个基本模式，但是“说题”怎么说，还是一个正在探索的问题.教师“说题”是一种类似于“说课”的教育教研展示和讨论活动，是“说课”的延续和创新，是深层次备课后的展示.开展“说题”，其宗旨是促进教师对试题的研究，从而把握高考命题的趋势与方向，用以指导课堂教学，提高课堂教学的针对性和有效性，同时，促进教师专业水平和自主学习能力的提升.作者认为，“说题”就是把命题立意、考纲要求、试题原型(在教材中的母题)、审题、分析、解答和试题变式的思维过程按一定规律及一定顺序说出来.本文以2018年全国卷Ⅱ理科19题为例进行“说题”分析.

一、高考真题

设抛物线C:y2=4x的焦点为F，过F且斜率为k(k>0)的直线l与C交于A,B两点，|AB|=8.

(Ⅰ)求l的方程；

(Ⅱ)求过点A,B且与C的准线相切的圆的方程.

二、考点分析与考纲要求

本题选自2018年全国卷Ⅱ理科第19题，考查的知识点是直线的方程、圆的方程、抛物线的定义、抛物线的标准方程、抛物线的简单几何性质、直线与抛物线的位置关系、直线与圆的位置关系.思想方面考查了数形结合思想、方程思想、化归与转化思想；另外还涉及了抽象概括能力和运算求解能力，解析几何与平面几何的交汇应用，数学运算、数学抽象等核心素养的考查，属中等偏上难度题目.

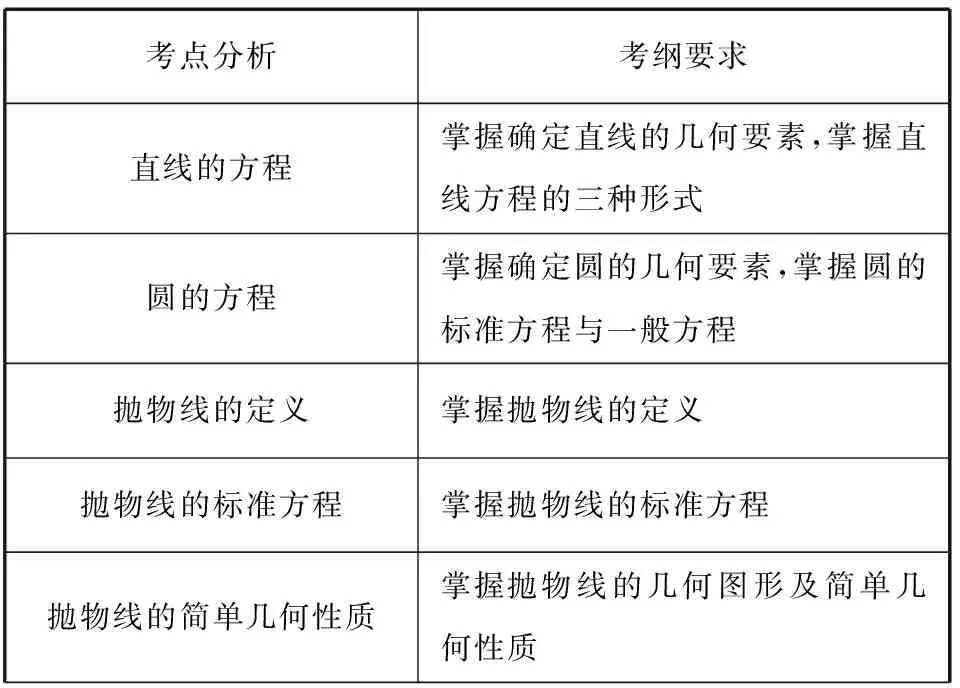
考点分析考纲要求直线的方程掌握确定直线的几何要素,掌握直线方程的三种形式圆的方程掌握确定圆的几何要素,掌握圆的标准方程与一般方程抛物线的定义掌握抛物线的定义抛物线的标准方程掌握抛物线的标准方程抛物线的简单几何性质掌握抛物线的几何图形及简单几何性质

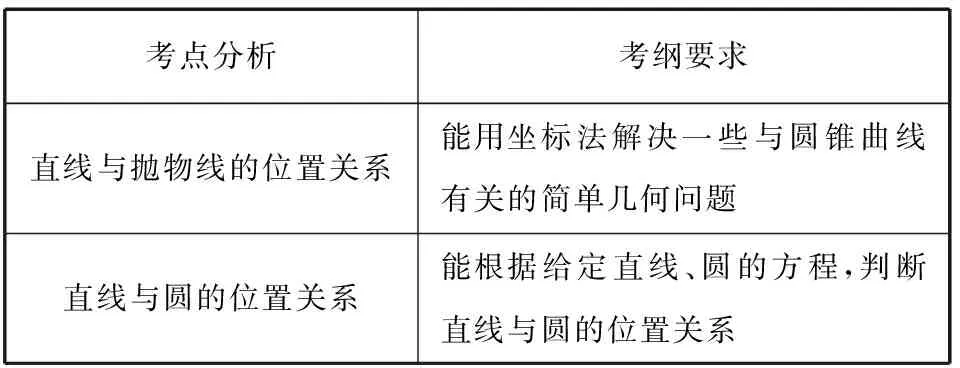
续表

三、教材原型

人教A版数学选修2-1第二章圆锥曲线与方程中2.4.2抛物线的简单几何性质第69页的例4.斜率为1的直线l经过抛物线y2=4x的焦点F，且与抛物线相交于A,B两点，求线段AB的长.

人教A版数学必修2第四章圆与方程中4.1.1圆的标准方程第120页的例3.

已知圆心为C的圆经过点A(1,1)和点B(2,-2)，且圆心C在直线l:x-y+1=0上，求圆心为C的圆的标准方程.

本题源自于以上两题的改编，本题第Ⅰ问将例4中的条件和结论交换，第Ⅱ问将例3中圆心C在直线l:x-y+1=0上改为圆与抛物线的准线相切.

四、真题分析

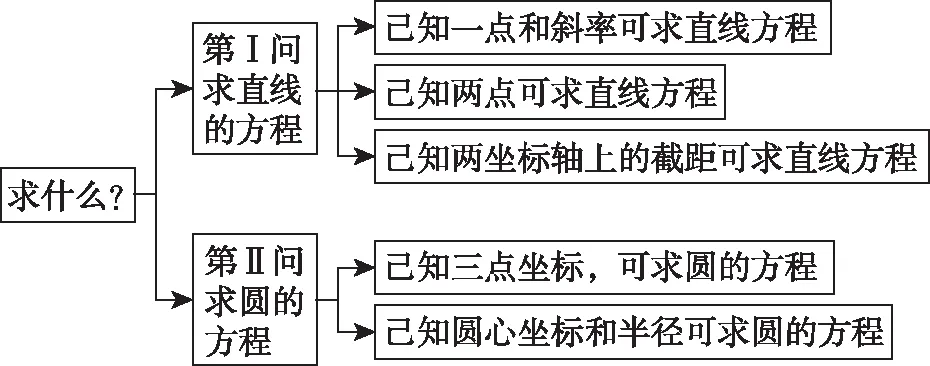
波利亚在《怎样解题》中将解决问题时的思维过程分成四个阶段——理解题目、拟订方案、执行方案、回顾，从而描绘出解题理论的一个总体轮廓，也组成了一个完整的解题教学系统，既体现常识性，又体现由常识上升为理论.所以解答问题时，需要经历两个关键过程，一是审题，二是解题.在审题时关键要抓住两个“什么”，即“有什么”和“是什么”的问题.对于本题，能找到哪些显现的已知条件？已知条件中又隐含着哪些本质关系？所以绘制以下审题思维导图：

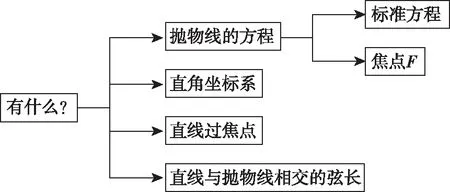
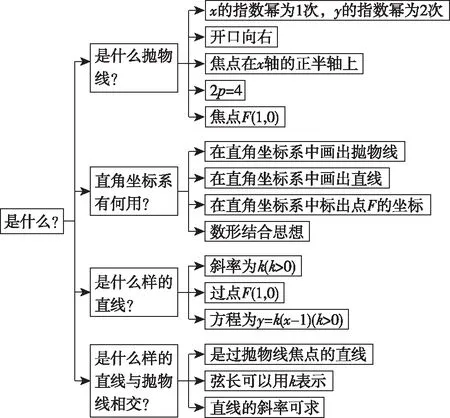
解题思维导图：

解法展示：

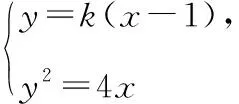
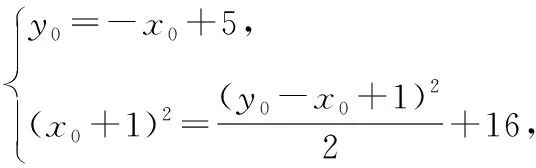
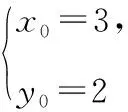
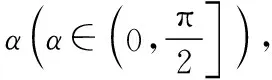
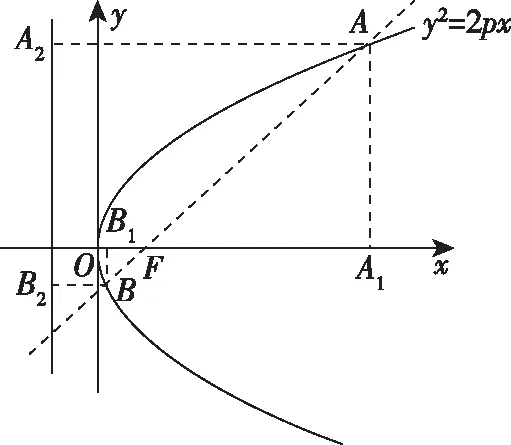
(Ⅱ)第二问同解法1.

五、真题变式

心理学研究表明，人的认识总是由浅入深，由表及里，由具体到抽象，由简单到复杂，因此，我们对一个题进行变式，就是对这个题更深入的研究，从而不断提升教师的专业素养.本题我们可以从以下几方面进行变式:(1)改变抛物线方程的形式;(2)若直线AB不过焦点，经过另一定点，求直线AB的方程；(3)改变设问的方式，如第一问可以变为求△AOB的面积；第二问可以变为证明以AF为直径的圆与y轴相切或证明以AB为直径的圆与准线相切；(4)将第二问作变式，过A，B两点作抛物线的切线，两切线交于一点P，证明点P的轨迹为一条直线.

六、反思总结

经过对题目的变式，我们发现对于著名的阿基米德三角形(抛物线的弦与过弦的两端点的两条切线所围成的三角形，这个三角形常被称为阿基米德三角形.)，当弦AB经过点F时，即为抛物线焦点弦的问题.