一道四川初赛试题的探源与拓展

四川 苏文玉

一、试题呈现

2016年四川高中数学竞赛初赛15题如下：

已知抛物线y2=2px过定点C(1,2)，在抛物线上任取不同于点C的一点A，直线AC与直线y=x+3交于点P，过点P作x轴的平行线交抛物线于点B.

(1)求证：直线AB过定点；

(2)求△ABC面积的最小值.

【解析】(1)由抛物线y2=2px过定点C(1,2)，可得抛物线方程为y2=4x.设直线AB的方程为x=my+a，与抛物线方程联立得y2-4my-4a=0.

设A(x1,y1),B(x2,y2)，则y1+y2=4m,y1y2=-4a.

P点坐标为(y2-3,y2)，因为AP过定点C，

化简得y1y2-2(y1+y2)+12=0，

将y1+y2=4m,y1y2=-4a代入上式，得a=-2m+3.

因此式对任意y1≠2都成立，因此直线x=my+a过定点Q(3,2).

(2)由(1)可设直线AB的方程为x=my-2m+3，

与抛物线方程联立得y2-4my+8m-12=0.则y1+y2=4m,y1y2=8m-12.

【评析】本题是一道初赛试题，主要考查抛物线的标准方程与几何性质、直线方程、直线与抛物线的位置关系等基础知识，考查推理论证能力、运算求解能力，考查数形结合、化归与转化、特殊与一般、分类与整合等数学思想.

二、试题探源

本题以抛物线为背景，通过共线、交点、平移得到的AB直线恒过定点，不禁让笔者思考如下几个问题：

1.本题中的点C和直线y=x+3是任意的吗？

2.本题的逆命题成立吗？或者变换本题的条件和结论，命题依然成立吗？

3.本题有更一般的结论吗?能够推广到其他圆锥曲线吗？

本着这样的研究思路，笔者在教材例题和历年高考试题中找到了本题的原型.

【探源1】(2001·全国卷理·19)设抛物线y2=2px(p>0)的焦点为F，经过点F的直线交抛物线于A，B两点.点C在抛物线的准线上，且BC∥x轴.证明直线AC经过原点O.

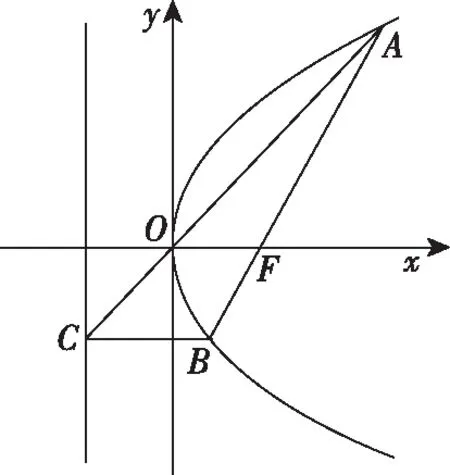
【探源2】(人教A版选修2-1第70页例5)过抛物线焦点F的直线交抛物线于A，B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.

从高考试题和教材上的例题可以看出，当定直线l为准线时，抛物线上的定点为坐标原点，则可得直线AB恒过焦点，同样，当AB恒过焦点时，可以证明A，O，C三点共线，可以证明BD和对称轴平行，还可以证明AO与过点B平行于对称轴的直线交点在定直线准线上.

那么定直线l和定点C是什么关系呢，经过研究发现，若抛物线在定点C处的切线与定直线l平行，则可得到下面更一般的结论.

三、拓展与探究

命题1：已知抛物线y2=2px(p>0)，点C为抛物线上任意点，设过点C的切线为l，已知定直线l′与l平行，在l′上任取点P，设PC与抛物线交于点A,过点P作对称轴的平行线交抛物线于点B,则直线AB过定点.

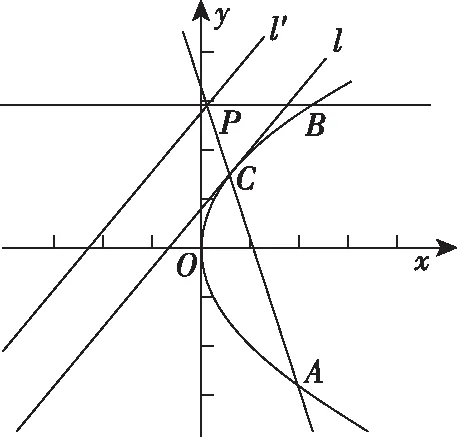
设直线AB:x=my+n,A(x1,y1),B(x2,y2)，

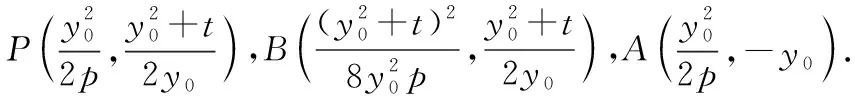
同样，我们可以得到下面的命题2—命题4.

命题2：已知抛物线y2=2px(p>0)，点C为抛物线上任意点，设过点C的切线为l，已知定直线l′与l平行，在抛物线上任取点A，设AC与l′交于点P,过P作对称轴的平行线交抛物线于点B,则直线AB过定点.

备注：命题2—命题4实际上是命题1变换条件和结论产生的新命题，证明方法与命题1一致，从结论来说，命题1—4分别从定点、定线和三点共线的角度对问题进行了揭示.值得思考的是，抛物线具有这样的性质，那么椭圆和双曲线是否也有类似的性质呢？由于与定直线平行的直线只有一条是与抛物线相切的，而椭圆和双曲线中，会有两条相切的直线与定直线平行，则会产生两个切点，那么又会有怎么样的结论呢？笔者对此问题进行了探究，得到了下面的一些结论.

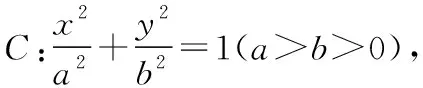
为了证明命题5是正确的，先证明下面一个引理.

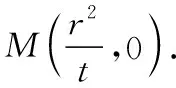
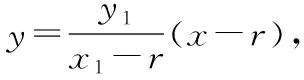
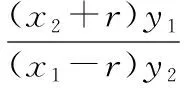
由引理的证明可知|OM||ON|=r2，且M在射线ON上.一般地，可以得到如下推论：

证明：由引理知AB恒过定点，

下面证明命题5.

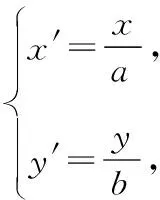
实际上，在椭圆中，容易证明M在过原点的直线C1C2上.

同样可以通过变换条件和结论给出下列命题6—8，证明留给读者.