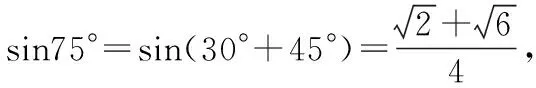教学考试杂志社“优师计划”阶段性成果展示
——高考重难点相关试题选登
【编者按】教学考试杂志社自发起“优师计划”以来,已经完成了诸多研究方向,涌现出一大批优秀团队的同时也研发出许多优秀成果.本期杂志从2019-2020年一系列的研发成果中精选出部分适合一轮复习阶段的优秀原创试题进行展示.同时欢迎更多教师加入“优师计划”,杂志社愿与更多的教师共同成长.
( )

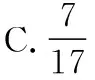
【答案】A
【考查角度】本题考查同角三角函数的基本关系、两角和与差的三角函数公式的运用,考查推理论证能力,考查逻辑推理、应用意识、数学抽象、数学运算的核心素养.


( )
A.1 B.2
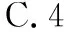
【答案】C
【考查角度】本题考查诱导公式、辅助角公式、特殊角的三角函数值、二倍角公式.

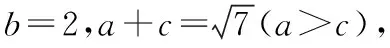

【考查角度】本题考查正弦定理、余弦定理,考查运算求解能力、数形结合思想,考查数学运算、直观想象的核心素养.


( )


【答案】B
【考查角度】本题考查基本不等式、正弦定理、余弦定理,考查推理运算能力,考查逻辑推理、数学运算的核心素养.

【易错点晴】正弦定理和余弦定理是高中数学中较为重要的知识点和考点.本题根据三角函数化简以及三角形面积公式得到面积最大值.

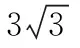
【考查角度】本题考查三角形正弦定理、余弦定理、三角形面积公式、三角函数变换及性质,考查推理论证、运算求解能力,考查逻辑推理、数学抽象核心素养.


6.【研发题】在△ABC中,若sinB恰好为sinA与sin(A+B)的等差中项,则角B的最大值为.
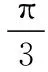
【考查角度】本题考查正弦定理、余弦定理和均值不等式的应用,考查推理论证、运算求解能力,考查逻辑推理、数学运算核心素养.

【教材链接】正弦定理、余弦定理:人教A版必修5 1.1.



【考查角度】本题考查基本不等式、正弦定理、余弦定理,考查推理运算能力,考查逻辑推理、数学运算核心素养.

【易错点睛】正弦定理和余弦定理是高中数学中较为重要的知识点和考点.本题利用三角函数化简、三角形面积公式并结合基本不等式得到面积最大值.
8.【研发题】(本小题满分12分)
△ABC的内角A,B,C的对边分别为a,b,c,a-bcosC=csinB.
(Ⅰ)求B;
(Ⅱ)若AC=2,求△ABC面积的最大值.
【考查角度】本题考查正弦定理、余弦定理、面积最值以及均值不等式的应用,考查逻辑推理、数学运算的核心素养.
(Ⅰ)首先利用正弦定理进行边角互化,再利用三角函数中两角和与差的正弦公式,辅助角公式,即可求得B;(Ⅱ)利用余弦定理、均值不等式求解即可或利用正弦定理、两角差的正弦公式结合辅助角公式求解即可.
【解题分析】(Ⅰ)由正弦定理知a=2RsinA,b=2RsinB,c=2RsinC(其中R为△ABC外接圆的半径),得2RsinA=2RsinBcosC+2RsinCsinB,
即sinA=sinBcosC+sinCsinB.
(2分)
又A=π-(B+C),
∴sinA=sin[π-(B+C)]=sin(B+C)
=sinBcosC+cosBsinC,
(4分)
即sinBcosC+cosBsinC=sinBcosC+sinCsinB,
∴cosBsinC=sinCsinB.
∵sinC≠0,∴cosB=sinB,且B为三角形内角,
(6分)
(Ⅱ)解法一:由余弦定理得b2=a2+c2-2accosB,
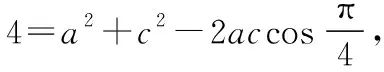

(8分)

(12分)
解法二:由正弦定理,
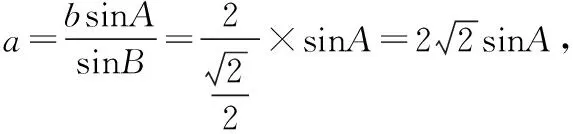



(12分)
9.【研发题】(本小题满分12分)

(Ⅰ)若a=2c=4,求边b的大小;

【考查角度】本题考查正弦定理与余弦定理的应用,考查运算求解能力,考查逻辑推理、数学运算的核心素养.

【解题分析】(Ⅰ)在△ABC中,由正弦定理可得
(1分)
(2分)

(3分)
由余弦定理得b2=a2+c2-2accosB=12,
(6分)
(Ⅱ)由cos(A+C)=cosAcosC-sinAsinC
(7分)
(9分)
∵b2=12,∴ac=4,
(10分)
(12分)
10.【研发题】(本小题满分12分)

(Ⅰ)若a=2c=4,求b;

【考查角度】本题考查正弦定理与余弦定理的应用,考查运算求解能力,考查逻辑推理的核心素养.
(Ⅰ)先根据已知条件可考虑用正弦定理,化边为角,求出一个确定的角B,再利用余弦定理即可求解;(Ⅱ)根据已知条件,考虑利用正弦定理可得b2=3ac,再由三角形面积公式即可解得△ABC的面积.
【解题分析】(Ⅰ)在△ABC中,由正弦定理可得
(1分)

在锐角△ABC中,
因为sinC>0,

(3分)

由余弦定理得b2=a2+c2-2accosB=12,

(6分)


(7分)


所以b2=3ac.
(9分)
因为b2=12,
所以ac=4,
(10分)

(12分)
11.【研发题】(本小题满分12分)
在△ABC中,内角A,B,C所对的边分别为a,b,c,
且m=(b-c,a),n=(b-c,-a),m·n=-bc.
(Ⅰ)求A的值;

【考查角度】本题考查正弦定理、余弦定理、平面向量的数量积、基本不等式等知识的综合应用.
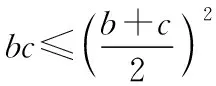
【解题分析】(Ⅰ)由m=(b-c,a),
n=(b-c,-a),
m·n=(b-c)(b-c)+(-a)a=-bc,
得b2+c2-a2=bc,
(2分)


(5分)
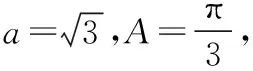
(7分)
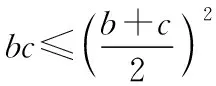
(8分)

(11分)


(12分)
【答题启示】对于含有a+b,ab及a2+b2的等式,求其中一个的范围时,可利用基本不等式转化为以该量为变量的不等式求解.
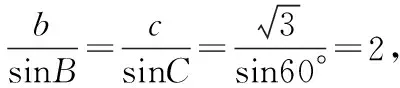
12.【研发题】(本小题满分12分)

(Ⅰ)求角B;
(Ⅱ)求△ABC的面积.
【考查角度】本题考查正、余弦定理和三角形面积公式在解三角形中的应用,考查运算求解能力和化归与转化的数学思想.
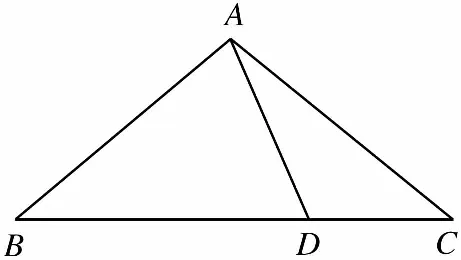
(Ⅰ)在△ADC中,利用余弦定理求∠ADC和∠ADB,在△ABD中利用正弦定理求角B;(Ⅱ)分别求△ABD和△ADC的面积,进而得到△ABC的面积.
【解题分析】(Ⅰ)在△ADC中,AD=5,AC=7,DC=3,
所以∠ADC=120°,∠ADB=60°.
(3分)

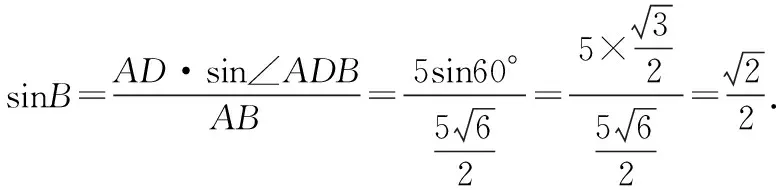
由题意知0° (6分) (Ⅱ)在△ABD中,由(Ⅰ)知∠BAD=75°, (12分) 13.【研发题】(本小题满分12分) 菱形ABCD的边长为2,∠ABC=120°,M,N为边AD,CD上两点,且∠MBN=90°. (Ⅰ)设DM=x,DN=y,求x,y之间的关系式; (Ⅱ)求MN的最小值. 【考查角度】本题考查余弦定理、勾股定理以及均值不等式的应用. (Ⅰ)在△ABM,△BCN,△DMN中,分别利用余弦定理得到BM2,BN2,MN2,然后在△MBN中利用勾股定理即可得到x,y满足的关系式;(Ⅱ)利用均值不等式,把x,y的关系式转化为x+y的不等式,解不等式即可求出x+y的最小值. 【解题分析】(Ⅰ)因为∠ABC=120°,则∠A=60°, 所以在△ABM中,由余弦定理得 BM2=4+(2-x)2-2×2(2-x)cos60° =4+x2-2x. (2分) 同理在△BCN和△DMN中, BN2=4+y2-2y. (3分) MN2=x2+y2-2xycos120°=x2+y2+xy. (4分) 又∠MBN=90°,则MN2=BM2+BN2, 所以(x+2)(y+2)=12或xy+2x+2y=8. (6分) (Ⅱ)由xy+2x+2y=8得 (8分) (10分) 则MN2=(x+y)2-xy =(x+y)2+2(x+y)-8 (11分) (12分)